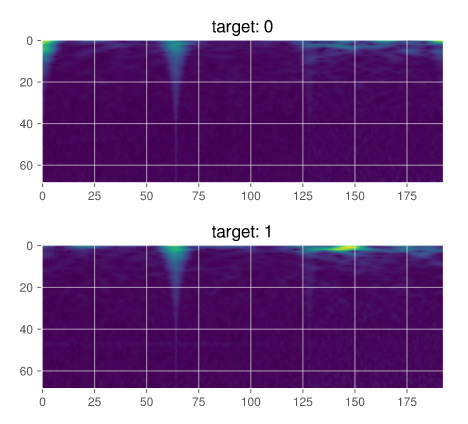
Constant-Q transform with Gravitational Waves Data

Constant Q-Transform

The constant quality factor transform (CQT), introduced by J.C. Brown in 1988, is an interesting alternative to the windowed Fourier transform (STFT / Short Time Fourier Transform) or wavelets, for time-frequency analysis.

The constant-Q transform transforms a data series to the frequency domain. It is related to the Fourier transform. In general, the transform is well suited to musical data and proves useful where frequencies span several octaves. It is more useful in the identification of instruments.

Unlike the Fourier transform, but similar to the mel scale, the constant-Q transform uses a logarithmically spaced frequency axis. For more information, read the original paper:

Judith C. Brown, “Calculation of a constant Q spectral transform,” J. Acoust. Soc. Am., 89(1):425–434, 1991.

From Wikipedia — In mathematics and signal processing, the constant-Q transform, simply known as CQT transforms a data series to the frequency domain. It is related to the Fourier transform[1] and very closely related to the complex Morlet wavelet transform. In general, the transform is well suited to musical data, and this can be seen in some of its advantages compared to the fast Fourier transform. As the output of the transform is effectively amplitude/phase against log frequency, fewer frequency bins are required to cover a given range effectively, and this proves useful where frequencies span several octaves. As the range of human hearing covers approximately ten octaves from 20 Hz to around 20 kHz, this reduction in output data is significant.

A Constant Q transform is a variation on the Discrete Fourier Transform (DFT). In other words, it is a type of wavelet transform.

I only have a casual understanding of both types of transforms myself, so take what I’m saying with a grain of salt.

A standard DFT uses a constant window size throughout all frequencies. This typically leads to a pretty consistent, fully continuous transform. However, the constant bin size for all frequencies leads to some problems when you map frequency on a logarithmic scale. Specifically, peaks on the lower end are incredibly wide (sometimes up to half an octave), lacking any sort of detail.

This is an issue for emulating human perception because humans perceive frequency on a logarithmic scale.

A Constant Q transform seeks to solve this problem by increasing the window size for lower frequencies, and alleviate some of the computational strain caused by this by reducing the window size used for high frequencies. It’s pretty effective at this, but has a few drawbacks.

The computational complexity of a Constant Q transform is only slightly larger than that of a standard DFT, but because the window size changes per frequency, it is impossible to apply the typical optimizations of the FFT to a Constant Q transform.

In other words, a Constant Q transform will yield better results where low frequencies and logarithmic frequency mapping are concerned.

The transform exhibits a reduction in frequency resolution with higher frequency bins, which is desirable for auditory applications. The transform mirrors the human auditory system, whereby at lower-frequencies spectral resolution is better, whereas temporal resolution improves at higher frequencies.

CQT refers to a time-frequency representation where the frequency bins are geometrically spaced and the Q-factors (ratios of the center frequencies to bandwidths) of all bins are equal.

nnAudio package

nnAudio is an audio processing toolbox using PyTorch convolutional neural network as its backend. By doing so, spectrograms can be generated from audio on-the-fly during neural network training and the Fourier kernels (e.g. or CQT kernels) can be trained. Kapre and torch-stft have a similar concept in which they also use 1D convolution from Keras and PyTorch to do the waveforms to spectrogram conversions. Other GPU audio processing tools are torchaudio and tf.signal. But they are not using the neural network approach, and hence the Fourier basis can not be trained.

From this Paper

“nnAudio, a new neural network-based audio processing framework with graphics processing unit (GPU) support that leverages 1D convolutional neural networks to perform time domain to frequency domain conversion. It allows on-the-fly spectrogram extraction due to its fast speed, without the need to store any spectrograms on the disk. Moreover, this approach also allows back-propagation on the waveforms-to-spectrograms transformation layer, and hence, the transformation process can be made trainable, further optimizing the waveform-to-spectrogram transformation for the specific task that the neural network is trained on. All spectrogram implementations scale as Big-O of linear time with respect to the input length. nnAudio, however, leverages the compute unified device architecture (CUDA) of 1D convolutional neural network from PyTorch, its short-time Fourier transform (STFT), Mel spectrogram, and constant-Q transform (CQT) implementations are an order of magnitude faster than other implementations using only the central processing unit (CPU).”

Implementation of a simple CQT Python code in Gravitational Wave Detection Kaggle Competition

Here’s the link to the main Kaggle competition.

I will be using the nnAudio package but first preparing the necessary data frame.

Now Function to show the CQT Spectogram

My YouTube Video Explaining the model building for Kaggle Submission for the Gravitational Wave Competition which includes Constant-Q transform related EDA