Data Representations For Neural-Networks Tensor Vector Scaler Basics
Link to Kaggle Notebook for this entire exercise
In general, all current machine-learning systems use tensors as their basic data structure. Tensors are fundamental to the field — so fundamental that Google’s TensorFlow was named after them. Even the text data or image data are converted to Numerical features for processing.
So what’s a tensor?
At its core, a tensor is a container for data — almost always numerical data. So, it’s a container for numbers. You may be already familiar with matrices, which are 2D tensors: tensors are a generalization of matrices to an arbitrary number of dimensions (note that in the context of tensors, a dimension is often called an axis).
Scalars (0D tensors)
A tensor that contains only one number is called a scalar (or scalar tensor, or 0-dimensional tensor, or 0D tensor). In Numpy, a float32 or float64 number is a scalar tensor (or scalar array). You can display the number of axes of a Numpy tensor via the ndim attribute; a scalar tensor has 0 axes (ndim == 0 ). The number of axes of a tensor is also called its rank. Here’s a Numpy scalar:
import numpy as npimport matplotlib.pyplot as plt
x = np.array(12)x
array(12)
Vectors (1D tensors)
An array of numbers is called a vector, or 1D tensor. A 1D tensor is said to have exactly one axis. Following is a Numpy vector:
x = np.array([12, 4, 6, 8, 14])
This vector has five entries and so is called a 5-dimensional vector. Don’t confuse a 5D vector with a 5D tensor! A 5D vector has only one axis and has five dimensions along its axis, whereas a 5D tensor has five axes (and may have any number of dimensions along each axis). Dimensionality can denote either the number of entries along a specific axis (as in the case of our 5D vector) or the number of axes in a tensor (such as a 5D tensor), which can be confusing at times. In the latter case, it’s technically more correct to talk about a tensor of rank 5 (the rank of a tensor being the number of axes), but the ambiguous notation 5D tensor is common regardless.
In another visual representation of Tensor
Matrices (2D tensors)
An array of vectors is a matrix, or 2D tensor. A matrix has two axes (often referred to rows and columns). You can visually interpret a matrix as a rectangular grid of numbers. This is a Numpy matrix:
x = np.array([[5, 78, 2, 34, 0],[6, 79, 3, 35, 1],[7, 80, 4, 36, 2]])
The entries from the first axis are called the rows, and the entries from the second axis are called the columns. In the previous example, [5, 78, 2, 34, 0] is the first row of x, and [5, 6, 7] is the first column.
3D tensors and higher-dimensional tensors
If you pack such matrices in a new array, you obtain a 3D tensor, which you can visually interpret as a cube of numbers. Following is a Numpy 3D tensor:
from numpy import arrayT = array([ [ [1,2,3], [4,5,6], [7,8,9]], [[11,12,13], [14,15,16], [17,18,19]], [[21,22,23], [24,25,26], [27,28,29] ], ])
print(T.shape)print("3D Tensor T is: ", T)print("Dimension of 3D Tensor T is: ", T.ndim)
(3, 3, 3)[[[ 1 2 3] [ 4 5 6] [ 7 8 9]] [[11 12 13] [14 15 16] [17 18 19]] [[21 22 23] [24 25 26] [27 28 29]]]3
See the output of the above, to understand the structure of a 3-D tensor. It is a collection of matrices. Thus unlike a single matrix with two axes a 3-D tensor has three axes.
By packing 3D tensors in an array, you can create a 4D tensor, and so on. In deep learning, you’ll generally manipulate tensors that are 0D to 4D, although you may go up to 5D if you process video data.
4-D tensors
The same way we get a 3-D tensor, if some of such 3-D tensors are to be grouped then another dimension gets created making the tensor a 4-D tensor. See the image for a hypothetical 4-D tensor. Here you can see three cubes are clubbed. Such 4-D tensors are very useful for storing images for image recognition in deep learning.
In the same fashion we can have more higher dimension tensors. Though tensors up to 4 dimension are more common, some times to sore videos 5-D tensors are also used. Theoretically there is no such limitation in dimension. For the sake of data storage in an organized manner any n number of dimensions can be used.
5-D tensors
This is the type of tensors when we need to store data with yet another dimension. Video data can be an ideal example where 5-D tensors are used.
If we take an example of a 5-minute video of 1080 HD resolution, then what will be the dimension of its data structure? Let’s calculate in a simple way. The pixel size will be 1080 x 1920 pixels. The time duration of the video in seconds is 5 x 60=300 seconds.
Now if the video is sampled by 10 frames/second then a total number of frames will be 300 x 10=3000. Suppose the colour depth of the video is 3. So for this video, the tensor should have 4 dimensions, the shape is (3000, 1080,1920,3).
So, the single video clip is a 4-D tensor. Now if we want to store multiple videos, say 10 video clips with 1080 HD resolution, then we need 5-D tensors. The shape of this 5-D tensor will be (3000, 1080,1920,3,10).
Key attributes of Tensors
A tensor is defined by three key attributes:
Number of axes (rank) — For instance, a 3D tensor has three axes, and a matrix has two axes. This is also called the tensor’s ndim in Python libraries such as Numpy.
Shape — This is a tuple of integers that describes how many dimensions the tensor has along each axis. For instance, the previous matrix example has shape (3, 5), and the 3D tensor example has shape (3, 3, 5). A vector has a shape with a single element, such as (5,), whereas a scalar has an empty shape, ().
Data type (usually called dtype in Python libraries) — This is the type of the data contained in the tensor; for instance, a tensor’s type could be float32, uint8, float64, and so on. On rare occasions, you may see a char tensor. Note that string tensors don’t exist in Numpy (or in most other libraries), because tensors live in preallocated, contiguous memory segments: and strings, being variable length, would preclude the use of this implementation. You can see all supported dtypes at tf.dtypes.DType.
To make this more concrete, let’s look back at the data we processed in the MNIST example. First, we load the MNIST dataset: This is a dataset of 60,000 28x28 grayscale images of the 10 digits, along with a test set of 10,000 images.
from keras.datasets import mnist
(X_train_images, Y_train), (X_test_images, Y_test) = mnist.load_data()
# To display the number of axes of the tensor X_train_images , the ndim attribute:
print(X_train_images.ndim)
# Here’s its shape:
print('shape of X_train_images', X_train_images.shape)
# And this is its data type, the dtype attribute:
print('dtypes ', X_train_images.dtype)
The MNIST dataset will be loaded as a set of training and test inputs (X) and outputs (Y). The imputs are samples of digit images while the outputs contain the numerical value each input represents.
So what we have here is a 3D tensor of 8-bit integers. More precisely, it’s an array of 60,000 matrices of 28 × 8 integers. Each such matrix is a grayscale image, with coefficients between 0 and 255.
Let’s display the fourth digit in this 3D tensor, using Matplotlib’s imshow function. Below are some details on this function from its official docs.
The input may either be actual RGB(A) data, or 2D scalar data, which will be rendered as a pseudocolor image. For displaying a grayscale image set up the color mapping using the parameters cmap=’gray’, vmin=0, vmax=255.
The number of pixels used to render an image is set by the axes size and the dpi of the figure.
A note on image size, pixel and numpy array
Images are made up of pixels and each pixel is a dot of color. Lets say I have a cat image of 1200×800 pixels. When an image is loaded into a computer, it is saved as an array of numbers. Each pixel in a color image is made up of a Red, Green and Blue (RGB) part. It can take any value between 0 and 255 with 0 being the darkest and 255 being the brightest. In a grayscale image, each pixel is represented by just a single number between 0 and 1. If a pixel is 0, it is completely black, if it is 1 it is completely white. Everything in between is a shade of gray.
So, if the cat image was black and white, it would be a 2D numpy array with shape (800, 1200). As it is a color image, it is in fact a 3D numpy array (to represent the three different color channels) with shape (800, 1200, 3).
Now to display our mnist image data as an image, i.e., on a 2D regular raster.
digit = X_train_images[4]
plt.imshow(digit, cmap=plt.cm.binary)
# plt.imshow just finishes drawing a picture instead of printing it. If you want to print the picture, you just need to add plt.show.
plt.show()
Let’s inspect a few examples of this MNIST dataset, containing only grayscale images.
I will use the subplot() funtion — The Matplotlib subplot() function can be called to plot two or more plots in one figure. Matplotlib supports all kind of subplots including 2x1 vertical, 2x1 horizontal or a 2x2 grid.
Here is the arguments for matplotlib.pyplot.subplots:
*args, (int, int, index)
Three integers (nrows, ncols, index). The subplot will take the index position on a grid with nrows rows and ncols columns. index starts at 1 in the upper left corner and increases to the right.
There is also an important difference between plt.subplots() and plt.subplot(), notice the missing 's' at the end.
We can use plt.subplots() to make all their subplots at once and it returns the figure and axes (plural of axis) of the subplots as a tuple. A figure can be understood as a canvas where you paint your sketch.
# create a subplot with 2 rows and 1 columns fig, ax = plt.subplots(2,1)
Whereas, you can use plt.subplot() if you want to add the subplots separately. It returns only the axis of one subplot.
fig = plt.figure() # create the canvas for plotting ax1 = plt.subplot(2,1,1) # (2,1,1) indicates total number of rows, columns, and figure number respectively ax2 = plt.subplot(2,1,2)
In many cases, plt.subplots() is preferred because it gives you easier options to directly customize your whole figure
# for example, sharing x-axis, y-axis for all subplots can be specified at once fig, ax = plt.subplots(2,2, sharex=True, sharey=True)
whereas, with plt.subplot(), one will have to specify individually for each axis which can become cumbersome.
fig = plt.figure()for i in range(9):
plt.subplot(3, 3, i+1)
plt.tight_layout()
plt.imshow(X_test_images[i], cmap='gray', interpolation='none')
plt.title("Digits: {}".format(Y_train[i]))
plt.xticks([])
plt.yticks([])
The parameter tight-layout to fit plots within your figure cleanly.
tight_layout automatically adjusts subplot params so that the subplot(s) fits in to the figure area. This is an experimental feature and may not work for some cases. It only checks the extents of ticklabels, axis labels, and titles.
An alternative to tight_layout is constrained_layout.
Manipulating tensors in Numpy
In the previous example, we selected a specific digit alongside the first axis using the syntax X_train_images[i] . Selecting specific elements in a tensor is called tensor slicing. Let’s look at the tensor-slicing operations you can do on Numpy arrays. The following example selects digits #10 to #100 (#100 isn’t included) and puts them in an array of shape (90, 28, 28):
my_slice = X_train_images[10:100]print(my_slice.shape)
It’s equivalent to this more detailed notation, which specifies a start index and stop index for the slice along each tensor axis. Note that : is equivalent to selecting the entire axis:
# The below slice notation with colon (:) is equivalent to the previous implementation
my_slice = X_train_images[10:100, :, :]
my_slice.shape
# Even the below slice notation with colon (:) is also equivalent to the previous implementation
my_slice = X_train_images[10:100, 0:28, 0:28]
my_slice.shape
A note on Python slice notation (:)
So what does the 3 mean in somesequence[::3] ?
: is the delimiter of the slice syntax to 'slice out' sub-parts in sequences , [start:end]
[1:5] is equivalent to "from 1 to 5" (5 not included)
[1:] is equivalent to "1 to end"
[len(a):] is equivalent to "from length of a to end"
Remember that [1:5] starts with the object at index 1, and the object at index 5 is not included.
The third parameter is the step. So, it means ‘nothing for the first argument, nothing for the second, and jump by three’. It gets every third item of the sequence sliced.
[::3] just means that you have not specified any start or end indices for your slice. Since you have specified a step, 3, this will take every third entry of something starting at the first index. For example:
'123123123'[::3]# '111'
a[start:stop] # items start through stop-1
a[start:] # items start through the rest of the array
a[:stop] # items from the beginning through stop-1
a[:] # a copy of the whole array
There is also the step value, which can be used with any of the above:
a[start:stop:step] # start through not past stop, by step
The key point to remember is that the :stop value represents the first value that is not in the selected slice. So, the difference between stop and start is the number of elements selected (if step is 1, the default).
The other feature is that start or stop may be a negative number, which means it counts from the end of the array instead of the beginning. So:
a[-1] # last item in the array
a[-2:] # last two items in the array
a[:-2] # everything except the last two items
Similarly, step may be a negative number:
a[::-1] # all items in the array, reversed
a[1::-1] # the first two items, reversed
a[:-3:-1] # the last two items, reversed
a[-3::-1] # everything except the last two items, reversed
Python is kind to the programmer if there are fewer items than you ask for. For example, if you ask for a[:-2] and a only contains one element, you get an empty list instead of an error. Sometimes you would prefer the error, so you have to be aware that this may happen.
Relation to slice() object
The slicing operator [] is actually being used in the above code with a slice() object using the : notation (which is only valid within []), i.e.:
a[start:stop:step]
is equivalent to:
a[slice(start, stop, step)]
Slice objects also behave slightly differently depending on the number of arguments, similarly to range(), i.e. both slice(stop) and slice(start, stop[, step]) are supported. To skip specifying a given argument, one might use None, so that e.g. a[start:] is equivalent to a[slice(start, None)] or a[::-1] is equivalent to a[slice(None, None, -1)].
While the :-based notation is very helpful for simple slicing, the explicit use of slice() objects simplifies the programmatic generation of slicing.
The notion of data batches
In general, the first axis (axis 0, because indexing starts at 0) in all data tensors you’ll come across in deep learning will be the samples axis (sometimes called the samples dimension). In the MNIST example, samples are images of digits. In addition, deep-learning models don’t process an entire dataset at once; rather, they break the data into small batches. Concretely, here’s one batch of our MNIST digits, with batch size of 128:
batch = X_train_images[:128]
And here’s the next batch:
batch = X_train_images[128:256]
And the n th batch:
batch = X_train_images[128 * n:128 * (n + 1)]
When considering such a batch tensor, the first axis (axis 0) is called the batch axis or batch dimension. This is a term we will frequently encounter when using Keras and other deep-learning libraries.
Real-world examples of data tensors
Let’s make data tensors more concrete with a few examples similar to what we will encounter generally. The data we will manipulate will almost always fall into one of the following categories:
Vector data — 2D tensors of shape (samples, features)
Timeseries data or sequence data — 3D tensors of shape (samples, timesteps, features)
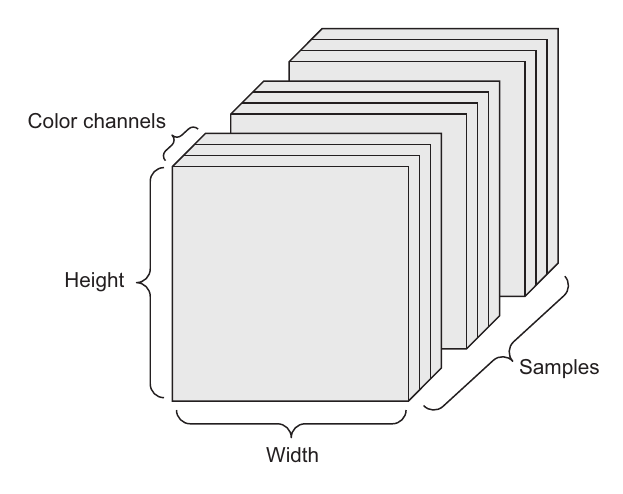
Images — 4D tensors of shape (samples, height, width, channels) or (samples, channels, height, width)
Video — 5D tensors of shape (samples, frames, height, width, channels) or (samples, frames, channels, height, width)
Vector data
This is the most common case. In such a dataset, each single data point can be encoded as a vector, and thus a batch of data will be encoded as a 2D tensor (that is, an array of vectors), where the first axis is the samples axis and the second axis is the features axis.
Let’s take a look at two examples:
An actuarial dataset of people, where we consider each person’s age, ZIP code, and income. Each person can be characterized as a vector of 3 values, and thus an entire dataset of 100,000 people can be stored in a 2D tensor of shape (100000, 3).
A dataset of text documents, where we represent each document by the counts of how many times each word appears in it (out of a dictionary of 20,000 common words). Each document can be encoded as a vector of 20,000 values (one count per word in the dictionary), and thus an entire dataset of 500 documents can be stored in a tensor of shape (500, 20000).
Timeseries data or sequence data
Whenever time matters in your data (or the notion of sequence order), it makes sense to store it in a 3D tensor with an explicit time axis. Each sample can be encoded as a sequence of vectors (a 2D tensor), and thus a batch of data will be encoded as a 3D tensor
The time axis is always the second axis (axis of index 1), by convention.
Let’s look at a few examples:
A dataset of stock prices. Every minute, we store the current price of the stock, the highest price in the past minute, and the lowest price in the past minute. Thus every minute is encoded as a 3D vector, an entire day of tradingencoded as a 2D tensor of shape (390, 3) (there are 390 minutes in a trading day), and 250 days’ worth of data can be stored in a 3D tensor of shape (250, 390, 3). Here, each sample would be one day’s worth of data.
A dataset of tweets, where we encode each tweet as a sequence of 280 characters out of an alphabet of 128 unique characters. In this setting, each character can be encoded as a binary vector of size 128 (an all-zeros vector except for a 1 entry at the index corresponding to the character). Then each tweet can be encoded as a 2D tensor of shape (280, 128), and a dataset of 1 million tweets can be stored in a tensor of shape (1000000, 280, 128).
Image data
Images typically have three dimensions: height, width, and color depth. Although grayscale images (like our MNIST digits) have only a single color channel and could thus be stored in 2D tensors, by convention image tensors are always 3D, with a one-dimensional color channel for grayscale images. A batch of 128 grayscale images of size 256 × 256 could thus be stored in a tensor of shape (128, 256, 256, 1), andbatch of 128 color images could be stored in a tensor of shape (128, 256, 256, 3)
The above is a 4D image data tensor (channels-first convention)
There are two conventions for shapes of images tensors: the channels-last convention (used by TensorFlow) and the channels-first convention (used by Theano). TensorFlow, places the color-depth axis at the end: (samples, height, width, color_depth). Meanwhile, Theano places the color depth axis right after the batch axis: (samples, color_depth, height, width). With the Theano convention, the previous examples would become (128, 1, 256, 256) and (128, 3, 256, 256). The Keras framework provides support for both formats.
Video data
As we mentioned earlier in this article, Video data is one of the few types of real-world data for which you’ll need 5D tensors.
A video can be understood as a sequence of frames, each frame being a color image. Because each frame can be stored in a 3D tensor (height, width, color_depth), a sequence of frames can be stored in a 4D tensor (frames, height, width, color_depth), and thus a batch of different videos can be stored in a 5D tensor of shape (samples, frames, height, width, color_depth).
For instance, a 60-second, 144 × 256 YouTube video clip sampled at 4 frames per second would have 240 frames. A batch of four such video clips would be stored in a tensor of shape (4, 240, 144, 256, 3). That’s a total of 106,168,320 values! If the dtype of the tensor was float32, then each value would be stored in 32 bits, so the tensor would represent 405 MB. Heavy! Videos we encounter in real life are much lighter, because they aren’t stored in float32, and they’re typically compressed by a large factor (such as in the MPEG format).