DMT-HI: MOE-based Hyperbolic Interpretable Deep Manifold Transformation for Unspervised Dimensionality Reduction
This paper is solving some long-standing problems in dimensionality reduction.
This paper is solving some long-standing problems in dimensionality reduction.
A new way to reduce data complexity while keeping important patterns visible.
DMT-HI combines hyperbolic geometry and expert models to make AI decisions more transparent
Think of it as giving AI a crystal-clear memory map of complex data.
Original Problem 🔍:
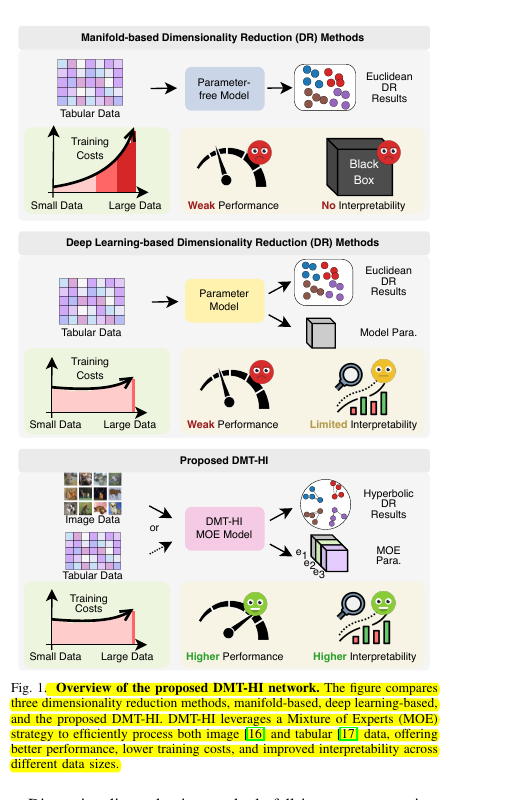
Traditional dimensionality reduction methods struggle to balance accuracy with interpretability when handling high-dimensional data. They often sacrifice one for the other, making it difficult to understand how the model makes decisions while maintaining performance.
DMT-HI shows us that we don't have to choose between performance and interpretability - we can have both.
Solution in this Paper 🛠️:
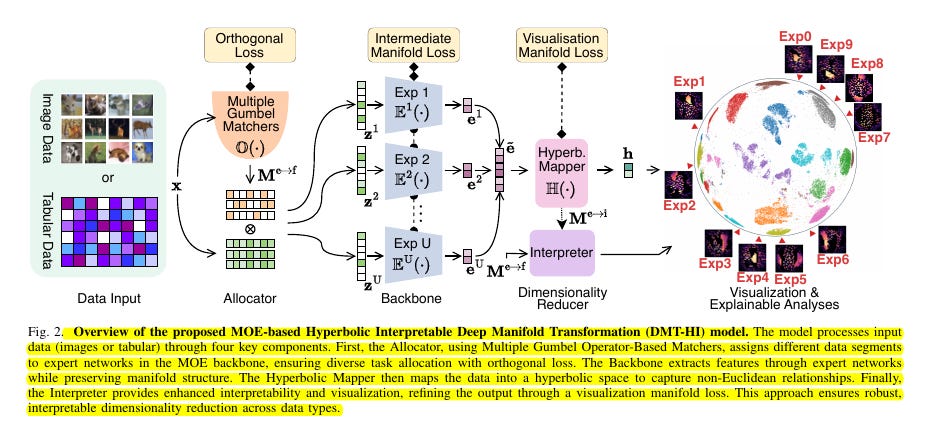
• Introduces DMT-HI (MOE-based Hyperbolic Interpretable Deep Manifold Transformation)
• Combines hyperbolic embeddings with Mixture of Experts (MOE) for dynamic task allocation
• Uses Multiple Gumbel Operator-Based Matchers for feature selection
• Implements hyperbolic mapping for better hierarchical structure capture
• Employs sub-manifold matching loss for preserving data relationships
• Features expert exclusive loss to promote diversity among expert representations
Key Insights 💡:
• Hyperbolic space better represents hierarchical data than Euclidean space
• MOE architecture improves both performance and interpretability
• Dynamic task allocation through Gumbel-Softmax enhances efficiency
• Clear mapping between input features and expert decisions enables transparency
Results 📊:
• Achieves 71.9% average classification accuracy on training (vs 61.2% baseline)
• Shows 69.8% accuracy on test sets (significant improvement over SOTA)
• Demonstrates superior performance on complex datasets (CIFAR-100: 39.1% vs 5.2% baseline)
• Maintains consistent performance across diverse data types (image, text, biological)
🔬 Key components of the DMT-HI architecture?
The model consists of:
Multiple Gumbel Operator-Based Matchers for task allocation
MOE network with specialized expert models
Hyperbolic Mapper for embedding data in hyperbolic space
Interpreter component for enhanced visualization and interpretability
🎯 How does DMT-HI improve over existing dimensionality reduction methods?
Uses hyperbolic embeddings to better capture complex hierarchical data structures
Implements MOE strategy to dynamically allocate tasks based on input features
Establishes clear connections between input data, embedding results and key features through the MOE structure
🎨 The interpretability of comes from:
Clear mapping between input features and expert models
Ability to track expert decisions and understand model workings
Explicit linking between raw data, embeddings and feature subsets
Enhanced visualization capabilities through hyperbolic space