Implementing RandomizedSearchCV from scratch
While Scikit-Learn offers two functions for implementing Hyperparameters Tuning with k-fold Cross Validations: GridSearchCV and RandomizedSearchCV, this post is about implementing a simplified version of RandomizedSearchCV with only pure Python.
Link to Full Notebook in Github
What Hyperparameter Tuning really is
Hyperparameter tuning refers to the shaping of the model architecture from the available space. In simple words, it is about searching for the right hyperparameter to find high precision and accuracy.
The most widely-used parameter optimizer techniques
Grid search
Random search
Hyperparameters vs Parameters
Parameters are the variables that are used by the Machine Learning algorithm for predicting the results based on the input historic data. These are estimated by using an optimization algorithm like Gradient Descent. Thus, these variables are not set or hardcoded by the Data Scientist. These variables are produced by model training. Example of Parameters: Coefficient of independent variables Linear Regression and Logistic Regression.
Hyperparameters are the variables that the Data Scientist specify usually while building the Machine Learning model. thus, hyperparameters are specified before specifying the parameters or we can say that hyperparameters are used to evaluate optimal parameters of the model.
For example, max_depth in Random Forest Algorithms, k in KNN Classifier.
Hyperparameters are not the model parameters
Hyperparameters are not the model parameters and it is not possible to find the best set of model-parameters from only the training dataset. Model parameters are learned during training when we optimise a loss function using something like a gradient descent.
In the GridSearch or RandomizedSearch tuning technique, we simply build a model for every combination of various hyperparameters and evaluate each model. The model which gives the highest accuracy wins. The pattern followed here is similar to the grid, where all the values are placed in the form of a matrix. Each set of parameters is taken into consideration and the accuracy is noted. Once all the combinations are evaluated, the model with the set of parameters which give the top accuracy is considered to be the best.
Grid Search
Grid Search uses a different combination of all the specified hyperparameters and their values and calculates the performance for each combination and selects the best value for the hyperparameters. This makes the processing time-consuming and expensive based on the number of hyperparameters involved.
Randomized Search
Random search is a technique where random combinations of the hyperparameters are used to find the best solution for the built model.
So The randomized search follows the same goal. However, we will NOT test sequentially all the combinations. Instead, we try random combinations among the range of values specified for the hyper-parameters. So here initially we specify the number of random configurations we want to test in the parameter space.
The main advantage is that we can try a broader range of values or hyperparameters within the same computation time as grid search, or test the same ones in much less time. We are however not guaranteed to identify the best combination since not all combinations will be tested.
This works best under the assumption that not all hyperparameters are equally important.
Grid Search vs Randomized Search
The only difference between both the approaches is in grid search we define the combinations and do training of the model whereas in RandomizedSearchCV the model selects the combinations randomly.
So when tuning for the best hyperparameter for a 2-dimensional space (i.e. optimizing two parameters), the process of grid search will look like as in Grid Search, we try every combination of a preset list of values of the hyper-parameters
But for the same 2-dimensional space (i.e. optimizing two parameters), the process of Randomized Search will be as below as Random search tries random combinations of a range of values (we have to define the number iterations).
K-Fold Cross-Validation in a Nutshell
The most popular type of Cross-validation is K-fold Cross-Validation. It is an iterative process that divides the train data into k partitions. Each iteration keeps one partition for testing and the remaining k-1 partitions for training the model.
The next iteration will set the next partition as test data and the remaining k-1 as train data and so on. In each iteration, it will record the performance of the model and at the end give the average of all the performances for that iteration.
Code Implementation of Randomized Search (accomodating only KNN Algorithm )
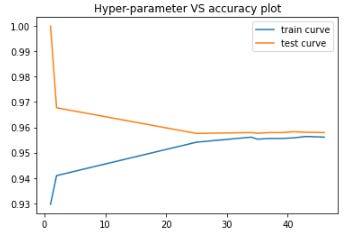
Plotting hyper-parameter vs accuracy plot
Now plotting hyper-parameter vs accuracy plot to choose the best
hyperparameter_ plt.plot(params['n_neighbors'], trainscores, label='train curve') plt.plot(params['n_neighbors'], testscores, label='test curve')
plt.title('Hyper-parameter VS accuracy plot')
plt.legend()
plt.show()
And we can see the best Test Accuracy is achieved around the k value of 42 and so that's the optimal hyperparameter that we should choose to apply KNN algorithm on this dataset.