Inference-Time Scaling for Diffusion Models beyond Scaling Denoising Steps -Google's breakthrough paper
Now, with a fixed inference compute budget, performing search on small models can outperform larger models without search.
Key Concepts
Diffusion models often rely on initial random noise to produce sample outputs. Some noises yield better generations than others. This observation motivates a search-based approach to optimize noise at inference time and achieve better outputs. The main idea is that not all random seeds are equally good, and systematically exploring them can produce higher-quality samples even without additional training.
A typical diffusion process involves iteratively denoising a latent variable starting from noise. Usually, we improve diffusion model outputs by just cranking up the number of denoising steps. Think of it like cleaning a noisy image - the more cleaning passes, the clearer the image becomes. But there's a catch: the improvement eventually plateaus, meaning extra steps won't help much after a certain point.
This paper introduces a totally different approach: inference-time scaling that treats the generation process as a search problem. Instead of just passively denoising, by relying solely on increasing denoising steps (measured in Number of Function Evaluations (NFEs)), the system actively searches for the best initial noise that will lead to a top-notch output. And this all happens without retraining the original, pre-trained model.
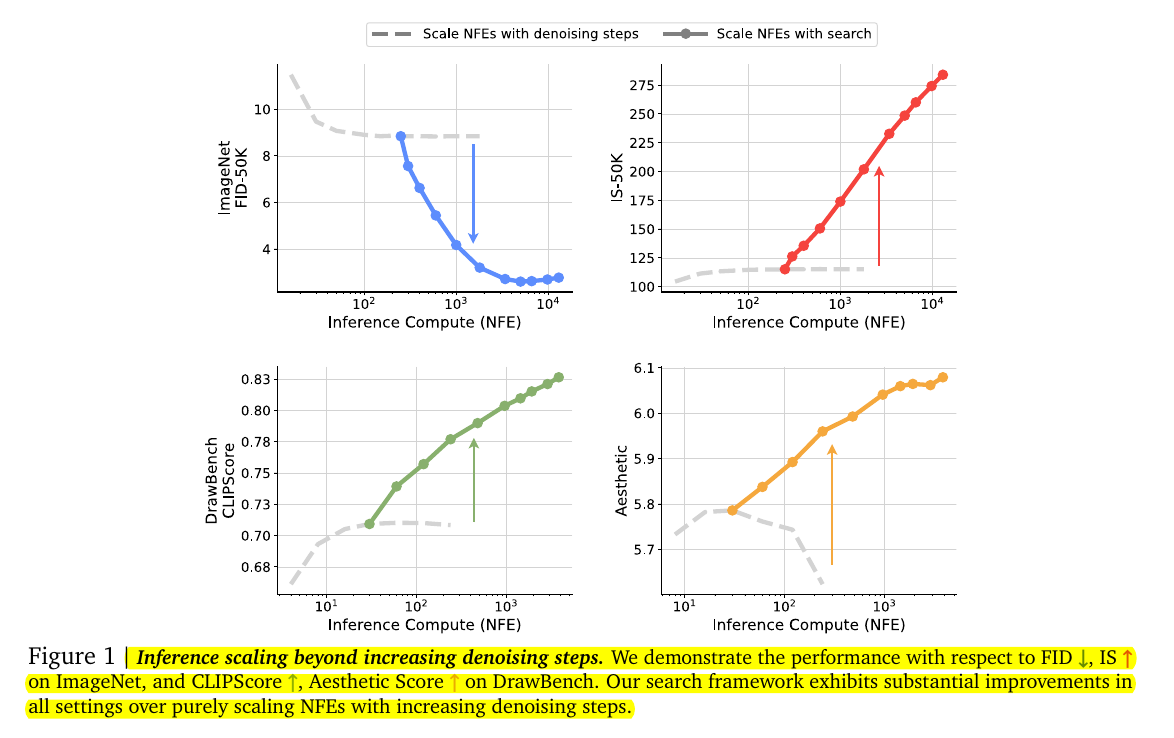
Scaling NFEs with denoising steps vs Scaling NFEs with Search
This figure compares two approaches to scaling inference compute (NFE) in diffusion models:
Scaling NFEs with denoising steps (dashed gray line): This refers to increasing the number of iterations used to denoise the sampled data.
Scaling NFEs with search (solid colored lines): This involves using additional compute to search for better noise candidates during sampling.
And we see that, in all four plots, where the solid lines (search method) show a much steeper improvement in performance with increasing compute compared to the dashed lines (denoising steps).
Top Left (ImageNet FID-50K): Lower FID values indicate better diversity and quality. Scaling with search achieves significantly better results than scaling denoising steps, especially in high NFE regimes, demonstrating the advantage of search.
Top Right (IS-50K): Higher Inception Scores indicate sharper and more discriminable samples. Scaling with search shows a clear advantage, with a steep improvement compared to the flat plateau of denoising step scaling.
Bottom Left (DrawBench CLIPScore): Higher scores indicate better alignment between text prompts and generated images. Search scaling leads to better alignment with the textual prompts, outperforming denoising step scaling.
Bottom Right (Aesthetic Score): Higher scores reflect better visual appeal. The search-based approach consistently yields better aesthetic quality as compute scales.
So, allocating NFEs to searching for better noises results in substantial improvements in generation quality, diversity, and alignment compared to simply increasing the number of denoising steps.
Visualizations of Scaling Behaviors
Left Three Columns (Increasing NFEs in Denoising Steps): These images demonstrate the results of progressively increasing the Number of Function Evaluations (NFEs) dedicated to denoising steps. The quality improves slightly with more denoising steps, but the improvements are subtle and eventually plateau.
Right Four Columns (Increasing NFEs in Search): These images show the results when NFEs are instead allocated to searching for better noise candidates. The improvements are much more pronounced. For example:
The lighthouse becomes more detailed and realistic, with better textures, lighting, and composition.
The hourglass evolves from a basic rendering to a visually compelling image with rich details and vibrant colors.
This section emphasizes that investing computational resources in search rather than merely increasing denoising steps leads to higher-quality outputs.
Why do I need Search, as proposed in this paper
In diffusion models, the initial noise plays a pivotal role in determining the quality of the generated samples. Not all initial noises are equally effective; some lead to higher-quality outputs than others. This phenomenon, often referred to as the "cherry-picking" effect, suggests that by searching for optimal initial noises, we can enhance the performance of diffusion models without modifying their architecture or retraining.
By focusing on optimizing this aspect, we can push the inference-time scaling limits, leading to more accurate and semantically faithful outputs without the need for extensive model retraining or architectural changes.
Now, the question is: if some noises are inherently better, do we really need these complex search techniques? Can't we just generate a bunch of samples and pick the best one (like literally "cherry-picking")?
The answer is yes, we can. But this is a very expensive, brute-force way to find a good noise. If you are generating thousands or tens of thousands of samples just to pick a good one, you are wasting a lot of compute.
This is exactly where this paper comes in. This paper goes beyond simple random search, and that's where its main contribution lies.
Key Proposal: Verifiers and Algorithms
At the heart of this new approach lies the concept of a search framework. This framework has two main components: verifiers and search algorithms.
Verifiers are like judges that evaluate the quality of generated images. The verifiers are crucial because they provide the feedback needed to guide the search algorithms. They provide feedback on how good a generated sample is. They can either rely on privileged information (like knowing the final evaluation metrics beforehand), use pre-trained models like CLIP, or use self-supervised methods that analyze the sample's internal consistency.
The choice of verifier depends on the specific task and what aspects of image quality we care about most. A verifier that focuses on aesthetic quality might lead to different results than one that prioritizes text-image alignment. It is also possible to combine different verifiers.
Search algorithms then use this feedback to find better starting "noise" inputs. We're not talking about the kind of noise you hear on an old radio - in this case, "noise" is just a random starting point for the generation process. Different search algorithms can be used, such as selecting the best noise out of a random bunch, iteratively refining a noise candidate, or exploring the noise space along the sampling path.
Three categories of verifiers are proposed:
Oracle Verifiers: Assume full privileged knowledge of the evaluation process. For instance, metrics like Fréchet Inception Distance (FID) directly measure the closeness of generated samples to the real data distribution.
Supervised Verifiers: Use pre-trained models aligned with specific tasks. Examples include CLIP and DINO, which evaluate alignment between image content and textual descriptions.
Self-Supervised Verifiers: Rely on intrinsic metrics, such as cosine similarity in feature spaces, which do not require labeled data.
Each verifier has biases depending on its training and evaluation design. Understanding these biases is critical when selecting verifiers for different tasks.
Similarly three search algorithms:
Random Search is the simplest method, selecting the best samples from a set of randomly generated candidates based on the verifier's score. This one-step strategy is computationally inexpensive but prone to overfitting to the verifier's biases, termed verifier hacking.
Zero-Order Search (ZO) refines noise candidates iteratively:
It starts with a pivot noise and generates candidates in its neighborhood.
Each candidate is scored using the verifier, and the highest-scoring noise becomes the new pivot.
This process repeats for a predefined number of iterations, reducing the risk of verifier hacking.
Search Over Paths explores intermediate sampling trajectories:
Initial noises are propagated to an intermediate state.
Variations are introduced at this stage, and the process continues towards the final output.
This method allows better exploration of the noise space while maintaining locality in the search.
Illustration of Search Algorithms
Random Search appears on the left as a tall curve, indicating all possible initial noises you might sample. Each red circle is a discarded candidate, and the single green circle is the one that scored best according to a chosen verifier. The idea is to generate many random noises, produce the corresponding images, and then only keep the highest-scoring one while rejecting the rest.
Zero-Order Search is shown in the middle with smaller pink dots surrounding a central pivot noise. Here the algorithm stays within a local “neighborhood” of a pivot noise, refining it gradually. Instead of sampling arbitrary points across the entire noise space, it explores small steps around the pivot based on feedback from the verifier, converging on better noises through repeated local updates.
Search over Paths on the right illustrates how the algorithm refines or branches out at multiple intermediate stages rather than only at the initial noise. The paper depicts extra sampling paths (those gray dotted lines) that grow as the sampler advances, with the best path at each step carried forward. This highlights a more dynamic and flexible way of exploring good samples by repeatedly injecting small changes along the trajectory, rather than solely focusing on the beginning noise.
This figure demonstrates the trade-offs between simplicity and sophistication in search strategies:
Random Search is straightforward but less effective in complex cases.
Zero-Order Search strikes a balance between efficiency and local refinement.
Search Over Paths leverages intermediate states to achieve superior performance, particularly in tasks requiring fine-grained control.
These algorithms highlight how compute resources can be optimally allocated during inference to improve the quality of diffusion model outputs.
By combining verifiers and search methods, the paper shows that scaling test-time compute can significantly enhance image fidelity. The search cost is measured in NFE (Number of Function Evaluations). While older diffusion research tries to reduce the total NFE to speed up generation, this new work flips the narrative by increasing NFE for quality gains instead of just boosting denoising steps.
In practice, each verifier has biases. For instance, Aesthetic Score might push images toward stylized looks but ignore faithfulness to the text prompt. CLIP-based verifiers might emphasize text alignment at the expense of aesthetics. When using a single verifier, over-optimization can degrade other metrics, known as verifier hacking. This phenomenon highlights that no single verifier works universally for all tasks.
To circumvent verifier hacking, the authors suggest techniques like Verifier Ensembling, where multiple verifiers produce ranks instead of direct scores, and the final selection is based on combined rankings. Ensemble verifiers help balance different visual attributes, reducing reliance on one biased measure.
Smaller diffusion models can also benefit from this approach. If a small model is computationally cheaper to run, it can be searched extensively to yield outputs that rival or surpass results from a bigger model. By employing extra inference-time compute, users can partially offset training costs and still reach high-quality outcomes.
Another important takeaway is that the chosen distance metric and step size for neighborhood sampling matter greatly. In Zero-Order Search, a step size that is too large can push the pivot noise too far from the original distribution, causing visual artifacts and mode collapse. A smaller step size is more conservative, yielding a steadier climb toward the local optimum but taking more iterations to converge.
Below is a small Python snippet that demonstrates a simplified random search for initial noise. This code is not from the paper itself but captures the core principle. It randomly samples initial noises, generates images, scores them, and returns the best noise.
The
generate_image_from_noisefunction:Applies the pre-trained diffusion_model to denoise a given noise tensor for a fixed number of steps.
Feeds the resulting image into a verifier to obtain a single numeric score indicating the sample’s quality.
The
random_searchfunction:Creates multiple candidate noise seeds, each of which could yield a different final image.
Loops over these noises, runs the diffusion process, and stores both the images and scores.
Locates the highest-scoring candidate and returns its noise and the corresponding image.
This approach can be extended to Zero-Order Search by adding small local perturbations around each pivot noise and evaluating verifiers iteratively. In code terms, one would replace the uniform random sampling of noise seeds with a function that creates neighbors in a local region, then pick the best pivot and repeat. That method can tighten the search around high-quality areas in noise space, preventing the diversity issues that random search might face if it invests too many tries blindly.
For text-to-image tasks, verifiers can rely on large pretrained networks like CLIP, which measure how well an image aligns with the text. Alternatively, an Aesthetic Verifier might rely on a neural network trained to predict human aesthetic preferences. The authors also tested advanced verifiers such as ImageReward that capture multiple criteria including alignment, aesthetic quality, and other human-centric judgments.
The experiments show that as we scale the number of forward passes used for searching, the quality steadily improves. One critical detail is that the final sampler’s denoising steps remain optimal (e.g. 30 or 250 steps), while additional compute is spent only on exploring better noise seeds. Large-scale experiments with FLUX.1-dev and ImageNet models reveal that additional search NFE can yield impressive boosts, sometimes surpassing bigger but search-free models.
The authors highlight that the exact “best” combination of verifier and search depends on the task. For instance, some tasks prioritize text alignment, while others demand more aesthetic or compositional accuracy. A general recommendation is to test multiple verifiers or use ensembles when the final goal is broad. Nevertheless, the fundamental idea stays the same: invest more compute in systematically finding better seeds instead of pushing the same seed through an even longer chain of denoising iterations.
By adopting this test-time scaling, diffusion models can be extended in ways similar to large language models’ iterative reasoning strategies. Instead of a single pass, the generative process explores multiple avenues, consistently improving outputs under constraints of user preference.
No single search configuration is universally optimal; each task instead necessitates a distinct search setup to achieve the best scaling performance
This figure shows the relative performance improvements in various evaluation metrics when using different verifiers for inference-time search with the FLUX-1.dev model. It compares the effectiveness of individual verifiers (Aesthetic, CLIPScore, ImageReward) and a Verifier Ensemble. The improvements are measured as a percentage gain over the baseline (generation without search).
Key Observations
Aesthetic Verifier:
Improves the Aesthetic score (+10.6%) but leads to slight reductions in CLIPScore (-2.2%) and ImageReward (-2.0%).
Focuses purely on enhancing visual appeal, often at the cost of text alignment and overall image quality.
CLIPScore Verifier:
Improves CLIPScore (+16.5%) and ImageReward (+24.1%) slightly, but the aesthetic score remains flat (+0.2%).
Prioritizes text-image alignment but lacks broader improvements in aesthetics.
ImageReward Verifier:
Provides the most significant gains in ImageReward (+64.3%) while moderately improving other metrics like CLIPScore (+3.6%) and Aesthetic (+0.2%).
Captures broader quality aspects such as alignment, aesthetics, and consistency.
Verifier Ensemble:
Combines all verifiers for balanced performance gains across metrics.
Substantial improvements in ImageReward (+46.6%), Aesthetic (+5.1%), CLIPScore (+9.1%), and LLM Grade (+4.5%).
Significance
This figure demonstrates that:
Different verifiers excel at optimizing specific attributes (e.g., Aesthetic Verifier for visual quality, ImageReward for overall preferences).
The Verifier Ensemble provides a balanced improvement across all metrics, making it the most versatile approach.
Allocating inference compute to search using targeted verifiers can significantly enhance sample quality in specific dimensions.
This framework has broad implications for both small and large diffusion models. Itshows that robust sample quality is not solely determined by model scale, but also by how test-time compute is allocated. For many use cases, devoting compute to search can reduce reliance on massive model sizes, which can mitigate deployment overhead and cut costs.