Language Models are Symbolic Learners in Arithmetic
The paper says, LLMs approach arithmetic as Position-based pattern matchers rather than computational engines.
The paper says, LLMs approach arithmetic as Position-based pattern matchers rather than computational engines.
So LLMs learn arithmetic through symbolic abstraction instead of mathematical calculations.
Original Problem 🔍:
LLMs struggle with basic arithmetic despite excelling in complex math problems. Previous research focused on identifying model components responsible for arithmetic learning but failed to explain why advanced models still struggle with certain arithmetic tasks.
Solution in this Paper 🛠️:
• Introduced a subgroup-level framework to analyze how LLMs handle arithmetic learning
• Broke down arithmetic tasks into two aspects:
👉 Subgroup complexity: measured through domain space size, label space entropy, and subgroup quality
👉 Subgroup selection: how LLMs choose input-output token mappings during training
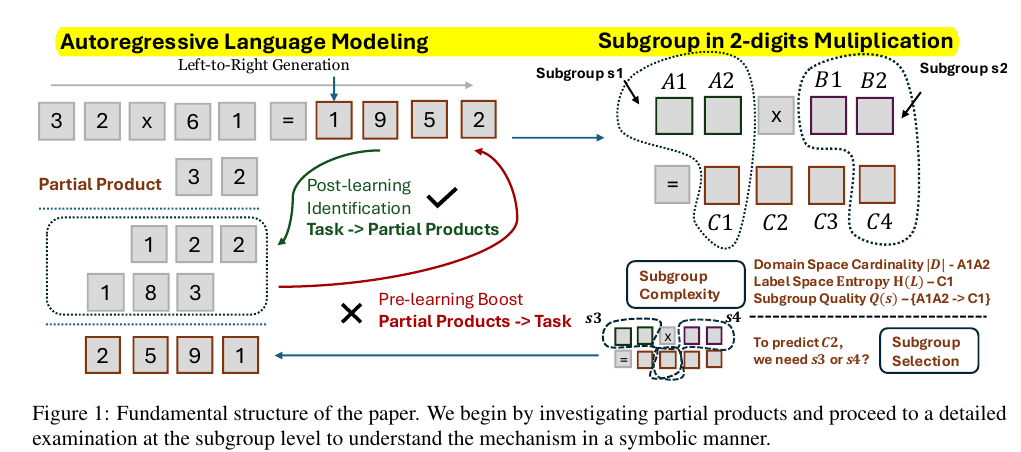
• Tested four different multiplication methods to investigate if LLMs use partial products
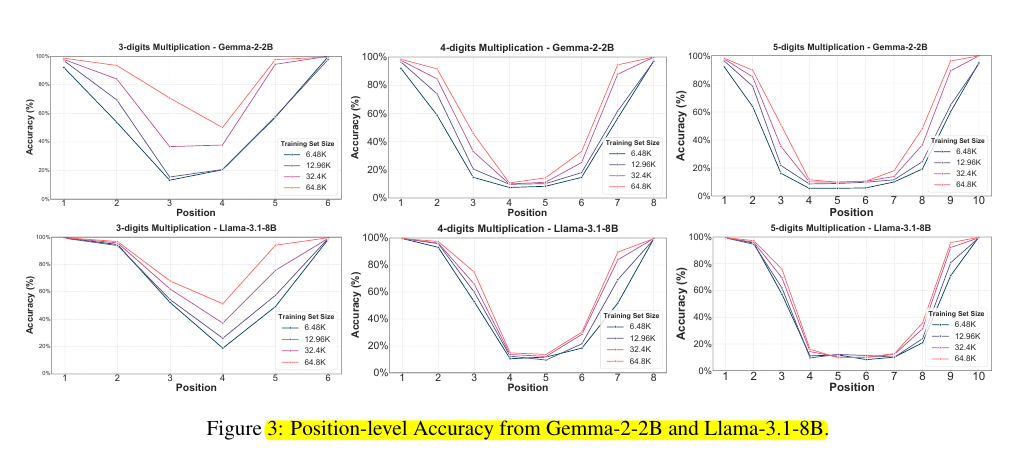
• Analyzed position-level accuracy across different training sizes
Key Insights 💡:
• LLMs don't perform actual calculations but function as pure symbolic learners
• Label space entropy is crucial for task complexity measurement
• LLMs show U-shaped accuracy curve - high accuracy (95%+) at first/last digits, low (<10%) in middle positions
• Models select subgroups following an easy-to-hard paradigm during learning
• Explicit training on partial products doesn't improve multiplication performance
Results 📊:
• Models improved in identifying partial products after training but failed to leverage them for calculations
• When subgroup complexity remained fixed, LLMs treated different arithmetic operations similarly
• Reducing entropy through modular operations improved accuracy
• Position-level accuracy followed consistent U-shaped pattern across different training sizes
• Both Gemma-2-2B and Llama-3.1-8B showed similar symbolic learning patterns
🧮 The way the paper investigate if LLMs use partial products for multiplication?
The researchers tested four different multiplication methods (standard multiplication, repetitive addition, lattice method, and Egyptian multiplication) and found that while LLMs could identify partial products after training, this ability did not help them perform better at multiplication tasks.
This showed LLMs weren't actually using partial products for calculations.
📈 LLMs show a U-shaped accuracy curve -
They quickly achieve high accuracy (95%+) for first and last digit positions, but struggle with middle digits (below 10% accuracy).
This suggests LLMs learn arithmetic by first mastering easier patterns at the edges before tackling harder patterns in the middle positions.
🔍 The subgroup-level framework proposed to understand LLM arithmetic learning
The paper breaks down arithmetic tasks into two key aspects:
Subgroup complexity - measured through domain space size, label space entropy, and subgroup quality
Subgroup selection - how LLMs choose the right mapping between input and output tokens during training.