Learn Beyond The Answer: Training Language Models with Reflection for Mathematical Reasoning
Reflective Augmentation (RefAug), proposed in this paper, trains LLMs to solve math by thinking deeply about alternative solutions
Reflective Augmentation (RefAug), proposed in this paper, trains LLMs to solve math by thinking deeply about alternative solutions
Original Problem 🔍 :
Existing data augmentation methods for mathematical reasoning focus on expanding training datasets, limiting models to single-round question-answering scenarios and neglecting deeper problem understanding.
Solution in this Paper 🧠 :
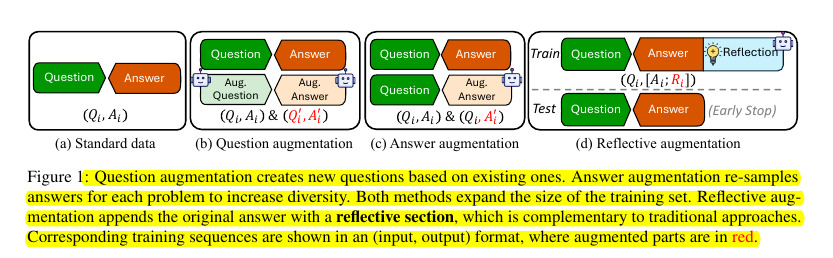
• Introduces reflective augmentation (RefAug) for LLMs
• Appends reflective sections to training instances:
Alternative reasoning: Different problem-solving approach
Follow-up reasoning: Abstraction or analogy of original problem
• Trains models to generate both original answer and reflective section
• Uses early stopping during inference for efficiency
Key Insights from this Paper💡:
• Reflection enhances deep understanding of math problems
• RefAug complements existing data expansion techniques
• Improves performance in both standard and reflective reasoning tasks
• Maintains inference efficiency through early stopping
Results 📊 :
• +7.2 accuracy gain over direct fine-tuning in single-round QA
• Significant improvement in reflective reasoning tasks:
+12.3 in follow-up QA (3rd round)
+22.3 in error correction
+10.6 in feedback utilization (5th round)
• Outperforms data expansion methods in reflective scenarios
• Synergistic benefits when combined with existing techniques
🧠 Reflective augmentation works by appending a reflective section to the original answer of each training instance.
This reflective section includes two components:
→ 1. Alternative reasoning: Presenting a different approach to solve the original problem.
→ 2. Follow-up reasoning: Either creating an abstraction of the original problem or devising an analogy to apply the concepts to a more complex situation.
The model is trained to generate both the original answer and the reflective section, but during inference, it only generates the answer.