Logic-of-Thought: Injecting Logic into Contexts for Full Reasoning in Large Language Models
Logic-of-Thought (LoT) enhances Chain-of-Thought’s performance on the ReClor dataset by +4.35%; moreover, it improves Chain-of-Thought with Self-Consistency’s performance on LogiQA by+5%; additionally
Logic-of-Thought (LoT) enhances Chain-of-Thought’s performance on the ReClor dataset by +4.35%; moreover, it improves Chain-of-Thought with Self-Consistency’s performance on LogiQA by +5%; additionally.
LoT prompting is like giving a smart assistant extra logical hints to help it reason better.
Original Problem 🔍:
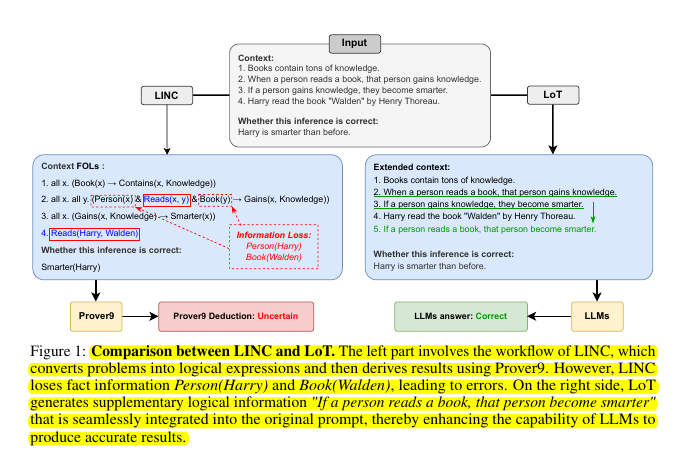
LLMs struggle with complex logical reasoning tasks due to unfaithful reasoning and information loss in existing neuro-symbolic methods.
Solution in this Paper 🧠:
• Logic-of-Thought (LoT) prompting:
Extracts propositions and logical expressions from input using LLMs
Expands expressions using logical reasoning laws
Translates expanded expressions back to natural language
Adds this as supplementary information to original prompt
• Integrates with existing methods: CoT, SC, CoT-SC, ToT
Key Insights from this Paper 💡:
• LoT preserves original context while adding logical guidance
• Avoids complete dependence on symbolic solvers
• Leverages LLMs' natural language understanding for potential error correction
• Orthogonal to and enhances existing prompting methods
The framework of Logic-of-Thought (LoT) consists of three main phases:
Logic Extraction:
Located on the left side of the diagram
Uses LLMs to extract propositions and logical relations from the input context
In this example, it identifies key propositions A, B, and C related to keyboarding skills, computer use, and essay writing
Extracts logical expressions like ¬A → ¬B and ¬B → ¬C
Logic Extension:
Positioned in the middle of the diagram
Applies logical reasoning laws to derive new logical expressions
Uses rules like Double Negation Law, Contraposition Law, and Transitive Law
Extends the initial logical expressions to derive C → A
Logic Translation:
Shown on the right side of the diagram
Utilizes LLMs to translate the extended logical expressions back into natural language
Converts C → A into "If you are able to write your essays using a word processing program, then you have keyboarding skills"
The process culminates in an extended context that includes the original input plus the newly derived logical information. This enhanced prompt is then fed back into the LLM for improved reasoning and answer generation.