🤯 Microsoft’S New rStar-Math Upgrades Small Models To Outperform OpenAI’s o1-Preview At Math
rStar-Math uses Monte Carlo Tree Search (MCTS) to generate and refine math solutions step by step. Instead of relying on large teacher models, it uses a smaller policy SLM (Small Language Model) to propose partial solutions and a Process Preference Model (PPM) to guide each step. This combo outperforms many larger models on challenging math benchmarks.
rStar-Math uses small language models (SLMs) (e.g., 1.5B, 3.8B, and 7B parameters) combined with a 7B Process Preference Model (PPM). Despite its smaller size, it achieves performance comparable to much larger models like GPT-o1-mini and Qwen2.5-Math-72B-Instruct.
How do they achieve this?
rStar-Math uses a math policy SLM for test-time search guided by an SLM-based process reward model.
Imagine you’re solving a math problem, and you’re not sure which path to take. rStar-Math uses Monte Carlo Tree Search (MCTS) to explore different ways to solve the problem. It’s like trying out different paths in a maze to find the best way out.
At each step, the model generates possible next steps (like writing down an equation or solving part of the problem) and checks if the step is correct by running a small piece of code. If the code runs successfully, the step is kept; otherwise, it’s discarded.
Performance and metrics
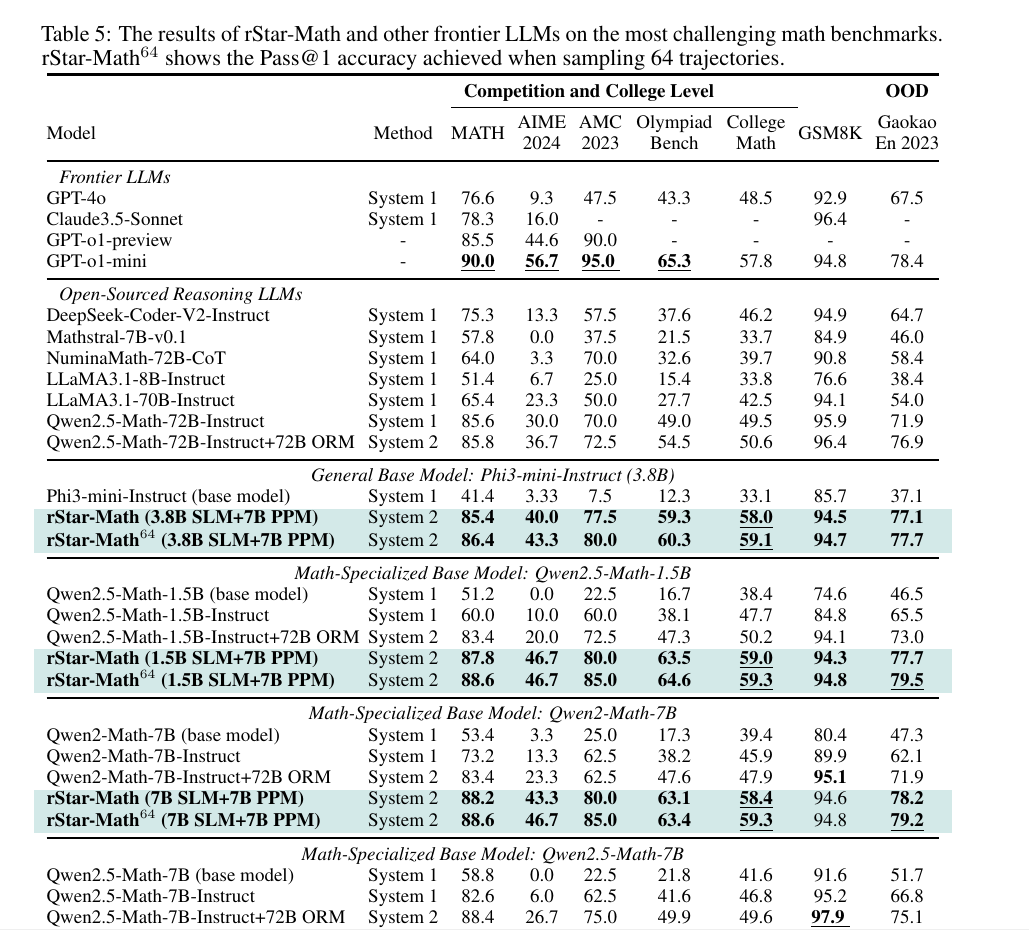
Key benchmarks showed that rStar-Math boosts Qwen2.5-Math-7B from 58.8% to 90% on MATH and 41.4% to 86.4% on Phi3-mini-3.8B.
→ On Olympiad-level math, it ranked among the top 20%, of high school competitors, solving 8 out of 15 problems on AIME 2024, outperforming most open-source models despite using only 7B-sized LLMs.
The implementations details
The pipeline begins by breaking down problems into smaller steps. The policy SLM suggests several candidate next steps (in text plus executable Python code). The system checks if the candidate’s Python code runs without errors. Each step gets a Q-value that measures how likely it leads to a correct final answer. Steps that improve the final correctness get higher scores.
The technique is called code-augmented Chain of Thought (CoT) because every textual step includes Python code. By verifying code execution, it discards broken or illogical steps. This filtering ensures only high-quality partial solutions remain. The more valid steps that lead to correct outcomes, the more confidence the model gains about its approach.
Monte Carlo Tree Search (MCTS) repeatedly refines these steps. Each rollout updates the Q-values for good or bad paths. Once enough rollouts occur, steps with stable positive Q-values stand out. These better steps are stored as verified reasoning data. Then the policy SLM trains on these new trajectories, learning to output more accurate steps in future rounds. This leads to self-improvement without giant teacher LLMs.
In MCTS, the Q-value represents the expected reward (or utility) of taking a particular action from a given state. It is calculated based on the outcomes of multiple rollouts (simulated trials). The Q-value essentially answers: "How good is this path based on past explorations?"
In each rollout, the policy model picks a partial step, and the system tracks whether continuing from that step leads to a correct final answer. If it does, the Q-value for that step increases; if it doesn’t, it decreases. Over multiple rollouts, these Q-values become more accurate because each path is tried enough times for the model to see patterns of success or failure.
By the end of MCTS, steps with stable positive Q-values are deemed higher quality. Their partial solutions then get stored as verified reasoning data, ensuring that only the most reliable paths train the policy model. This process gradually boosts the policy model’s ability to produce step-by-step solutions with fewer errors.
A key component is the Process Preference Model (PPM), which assigns a reward-like signal to each partial step. Unlike an outcome-based reward model that only cares about correct final answers, the PPM focuses on each intermediate step. The training data for the PPM comes from MCTS: correct step paths get labeled as positive, and incorrect ones get labeled as negative. This ranking approach helps the PPM judge the steps more reliably.
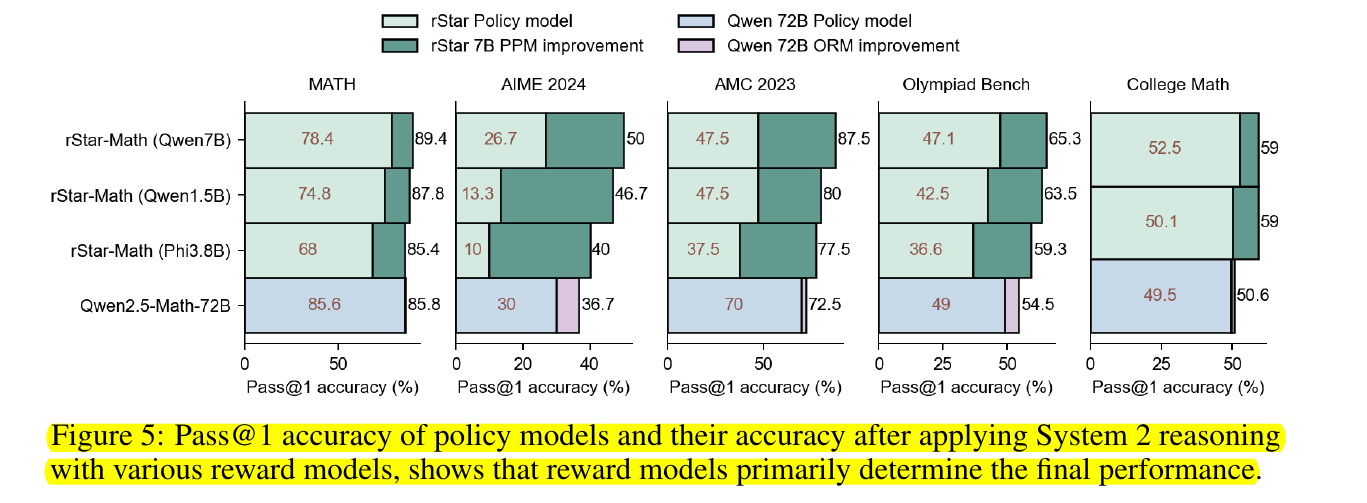
Pass@1 accuracy of policy models and their accuracy after applying System 2 reasoning with various reward models, shows that reward models primarily determine the final performance
This figure contains five side-by-side charts (for MATH, AIME 2024, AMC 2023, Olympiad Bench, and College Math), and each chart compares different model setups. Each bar is a stacked bar that shows two primary values: the lower segment is the baseline policy model’s Pass@1 accuracy, and the upper segment is how much that accuracy improves when System 2 reasoning (MCTS) is applied with a reward model.
Pass@1 accuracy is a metric used to evaluate how often a model provides a correct answer on the first attempt. In the context of tasks like math reasoning or code generation, if a model generates multiple possible answers or reasoning paths, Pass@1 focuses only on whether the very first attempt was correct.
In the leftmost set (MATH), for example, rStar-Math (Qwen7B) has a bottom segment labeled 78.4, meaning the policy-only accuracy is 78.4%. Above it, the bar extends to 89.4, which is the final Pass@1 after the rStar 7B PPM is used for step-by-step verification. A similar pattern appears for rStar-Math (Qwen1.5B) and rStar-Math (Phi3.8B), where the upper portion indicates how much the PPM bumps up their scores. On the Qwen2.5-Math-72B bars, the baseline and final values are very close, showing smaller improvement from that model’s 72B ORM.
System 2 reasoning here means generating multiple solution paths using MCTS and then selecting the best one based on a reward model. The figure highlights that Process Preference Models (PPM) or advanced Outcome Reward Models (ORM) can dramatically boost final performance. Even if the underlying policy model’s baseline score is low, combining it with a strong reward model can push the overall accuracy closer to top-tier results.
The core takeaway is that the policy model alone has a certain baseline accuracy, but reward models like PPM or ORM boost performance substantially when used with test-time MCTS. The figure emphasizes that even if a policy model starts with modest performance, having a strong process reward (PPM) can raise the final accuracy to levels comparable or beyond much larger models.
The rightmost group (College Math) shows smaller baseline bars with big improvements from reward models, illustrating that the reward model primarily drives the final accuracy. By comparing the lighter segments (policy alone) to the darker cumulative bars (policy plus reward), one sees the huge gap in performance that reward feedback closes. This underscores the paper’s central claim that well-trained step-level or outcome-level reward models are key to unlocking advanced math solving capabilities in smaller models.
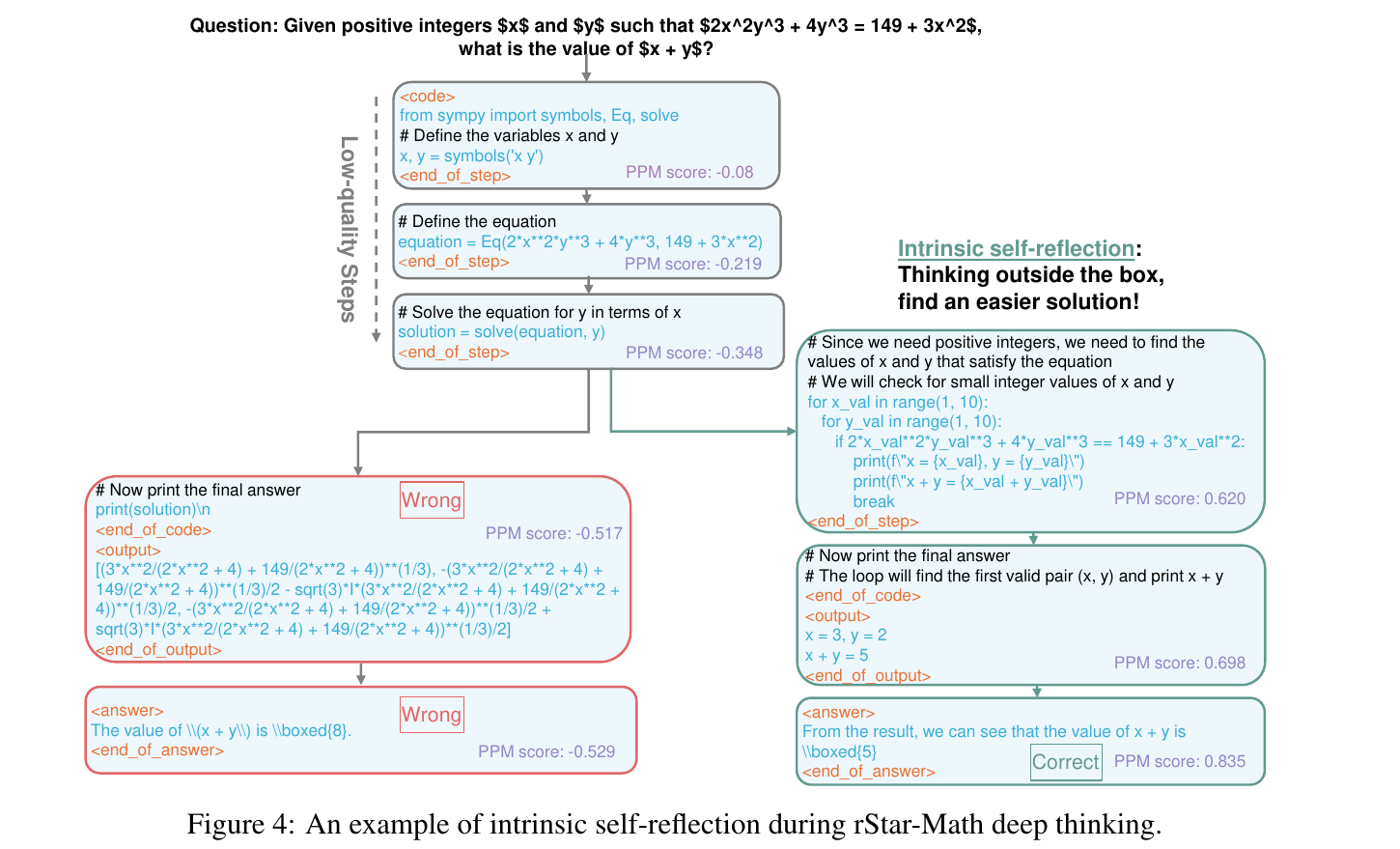
Example of intrinsic self-reflection during rStar-Math deep thinking.
rStar-Math uses MCTS to try out different solution paths, like testing routes in a maze. At each step, it generates reasoning (with Python code), runs the code to check correctness, and discards invalid steps. It tracks progress using PPM scores to favor paths that lead to correct answers, backtracking and switching approaches when needed until it finds the optimal solution.
The system begins with an incorrect approach by defining symbolic equations using Python's sympy library, attempting to solve for x and y in terms of algebraic expressions. The initial steps receive progressively low PPM scores as the solution path diverges from the correct result.
1. Problem Statement:
The system is asked to solve for x + y where the equation is:
2x^2y^3 + 4y^3 = 149 + 3x^2
The values for x and y must be positive integers.
Stage 1: The Initial Approach (Wrong Path)
Step 1:
The policy model begins by importing
sympyto symbolically represent variablesxandy.A Python code block defines the equation.
PPM score:
-0.08, indicating low confidence.
Step 2:
The model forms the full equation using
sympy’sEq()function to build an expression for solving.PPM score:
-0.219, indicating that the step doesn’t seem promising.
Step 3:
The system attempts to solve the equation for
yin terms ofxusing thesolve()function.The PPM assigns a worse score of
-0.348, indicating a further decline in quality.
Step 4:
The system prints out a symbolic solution.
The output contains a complex set of symbolic solutions, including cube roots and imaginary terms, which don’t satisfy the requirement for positive integers.
Final PPM score:
-0.517, signaling that this is a dead-end path.
→ Result: The system outputs the incorrect value of x + y = 8.
Stage 2: Self-Reflection and Backtracking
rStar-Math recognizes that it’s on a low-quality reasoning path based on poor PPM scores.
Stage 3: The Simpler Brute-Force Solution (Correct Path)
Step 1:
Instead of continuing with symbolic algebra, the system switches to a brute-force method.
It iterates over small integer values for
xandy(from 1 to 10) and checks if they satisfy the equation.
Step 2:
The first valid pair
(x = 3, y = 2)is found, satisfying the equation.PPM score:
0.620, indicating higher confidence.
Step 3:
The sum
x + y = 5is calculated and output as the answer.The final PPM score:
0.835, confirming the model’s confidence that this is correct.
→ Final Answer: 5.
The key takeaway is that rStar-Math recognizes the failure of its initial path through the PPM's negative feedback. Instead of continuing down the flawed path, it backtracks and finds a simpler brute-force solution by iterating over small integer values for x and y. This approach quickly identifies the correct pair (x=3, y=2), leading to the correct answer x + y = 5.
The point being demonstrated: rStar-Math’s MCTS-based reasoning can revise its approach mid-solution based on step-level evaluation, showcasing an emerging capability of self-correction and adaptability.
In a broader sense, each search iteration uses PPM-augmented MCTS. The model selects expansions (new steps) that the PPM judges to be high-quality. Each candidate’s code block is executed. If the final step matches the known correct answer, that entire solution path is labeled as a successful sequence. This fosters a cycle of generating, validating, and then learning from the best data.
Self-evolution happens over multiple rounds, each time improving both the policy SLM and the PPM. Early rounds might produce fewer correct solutions, but each new round grows the coverage of successful math problems. By the end, the approach achieves state-of-the-art results on benchmarks such as MATH, AIME, and Olympiad-level problems, all with small model sizes.
Monte Carlo Tree Search (MCTS) for scaling test-time computation (i.e., exploring more reasoning paths) for better performance.
MCTS happens after the policy model is already trained and is used at inference time to explore multiple paths. It systematically branches out different solutions, updating Q-values as it finds correct or incorrect endpoints. This is a classic form of test-time computation because it involves additional compute during inference rather than just running a single pass.
Scaling test-time computation means letting the model analyze more solution trajectories, which boosts the chance of reaching a correct answer. MCTS amplifies this effect by pruning low-quality paths and reinforcing high-quality ones, refining the final solution. By dedicating extra inference cycles to iterative search, the model gains a more thorough look at potential reasoning chains, improving its math accuracy beyond a single forward pass.
Overall it shows so much alpha left in algo. With the right technique, we don't need massive models for complex tasks.