miniCTX: Neural Theorem Proving with (Long-)Contexts
Neural theorem provers now understand mathematical context by learning from complete mathematical files instead of isolated theorems.
Neural theorem provers now understand mathematical context by learning from complete mathematical files instead of isolated theorems.
So the paper proposes to prove theorems by showing the model, the entire mathematical environment, not just individual problems.
Original Problem 🎯:
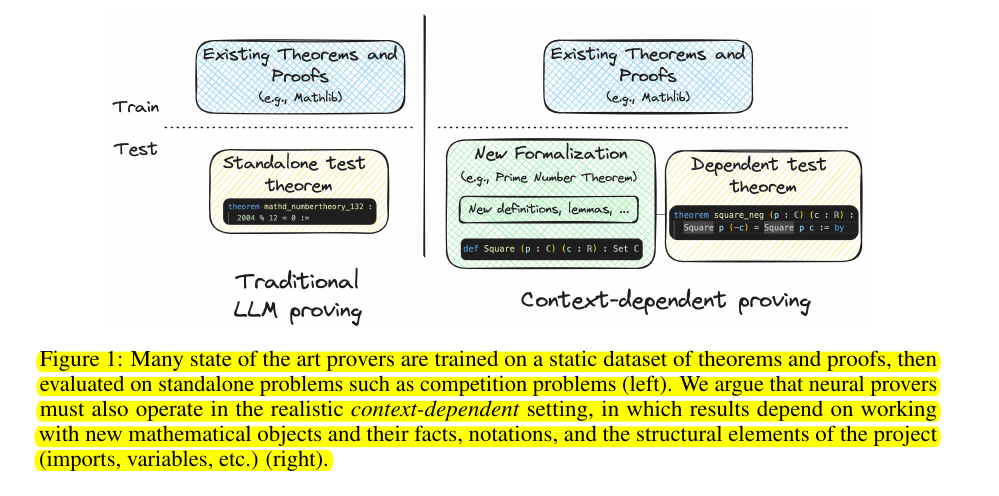
Current neural theorem provers struggle with real-world formal theorem proving that requires understanding new context, definitions, and project-specific constraints. Existing methods often fail to incorporate the full range of contextual information available in real-world projects.
Solution in this Paper 🛠️:
• Introduced miniCTX: A benchmark to evaluate neural theorem provers' ability to handle context-dependent theorem proving
• Created NTP-TOOLKIT: Automatically extracts and annotates theorem proving data from Lean projects
• Developed file-tuning method: Trains models using full file contexts, where both theorem statements and surrounding context are provided
• Implemented premise selection: Retrieves relevant premises from imported modules to supplement in-file context
• Tests three levels of generalization: theorem-level, context-level, and project-level
Key Insights from this Paper 💡:
• Real-world theorem proving heavily depends on context beyond just premises
• Models need to adapt to new definitions, lemmas, and project constraints
• File-tuned models significantly outperform traditional state-tactic models
• Premise selection helps but can interfere with in-file context processing
• Models heavily rely on automation tactics for proof generation
Results 📊:
• File-tuned models achieved 35.94% success rate vs 19.53% for state-tactic models
• GPT-4 with context showed 27.08% success vs 11.72% without context
• Performance drops when automation tactics are disabled (27.45% vs 41.18%)
• Models struggle with longer proofs (>5 lines) showing only 19% success rate
🎯 How does miniCTX differ from existing theorem proving benchmarks?
miniCTX is unique in several ways:
It includes full context beyond just premises, incorporating definitions, prior proofs, comments, notations, and structural components
It sources theorems from multiple real-world projects and textbooks
It ensures temporal splits to prevent data contamination
It tests three levels of generalization: theorem-level, context-level, and project-level