Read time: 6 min
📚 Browse past editions here.
( I publish this newletter daily. Noise-free, actionable, applied-AI developments only).
⚡In today’s Edition (16-Jun-2025):
🤖 MIT Unveil A New Step Towards Self-Improving AI, LLMs self-edit to 72.5% accuracy
🧑🎓 Deep Dive: Understanding Muon optimizer. Training heavy transformers finishes sooner because gradients stop looping on same axes.
🤖 MIT Unveil A New Step Towards Self-Improving AI, LLMs self-edit to 72.5% accuracy
MIT introduces SEAL (Self-Adapting LLMs), a framework enabling LLMs to self-edit and update their weights via reinforcement learning.
⚙️ The Details
→ The core idea behind SEAL is to enable language models to improve themselves when encountering new data by generating their own synthetic data and optimizing their parameters through self-editing. The model’s training objective is to directly generate these self-edits (SEs) using data provided within the model’s context.
Each self-edit is a text directive that specifies how to make synthetic data and set hyperparameters for updating weights.
The generation of these self-edits is learned through reinforcement learning. The model is rewarded when the generated self-edits, once applied, lead to improved performance on the target task.
Therefore, SEAL can be conceptualized as an algorithm with two nested loops: an outer reinforcement learning (RL) loop that optimizes the generation of self-edits, and an inner update loop that uses the generated self-edits to update the model via gradient descent.
An outer reinforcement loop rewards self-edits that improve downstream accuracy, while an inner supervised loop applies each edit.
This method can be viewed as an instance of meta-learning, where the focus is on how to generate effective self-edits in a meta-learning fashion.
📊 Empirical Gains:
Across domains, self-generated data always beats raw data or human-prompted synthetic data, confirming that the model’s own rephrasing is easier for it to learn.
Lightweight LoRA updates make each inner loop quick, so a single GPU pair can run the whole process in a few hours. In knowledge tasks SEAL boosts QA performance. Fine-tuning on self-generated implications raises no-context SQuAD accuracy to 47.0%, surpassing GPT-4.1 synthetic data.
→ In few-shot puzzles SEAL chooses augmentations and hyperparameters automatically. This lifts success rate from 0% to 72.5% after RL training.
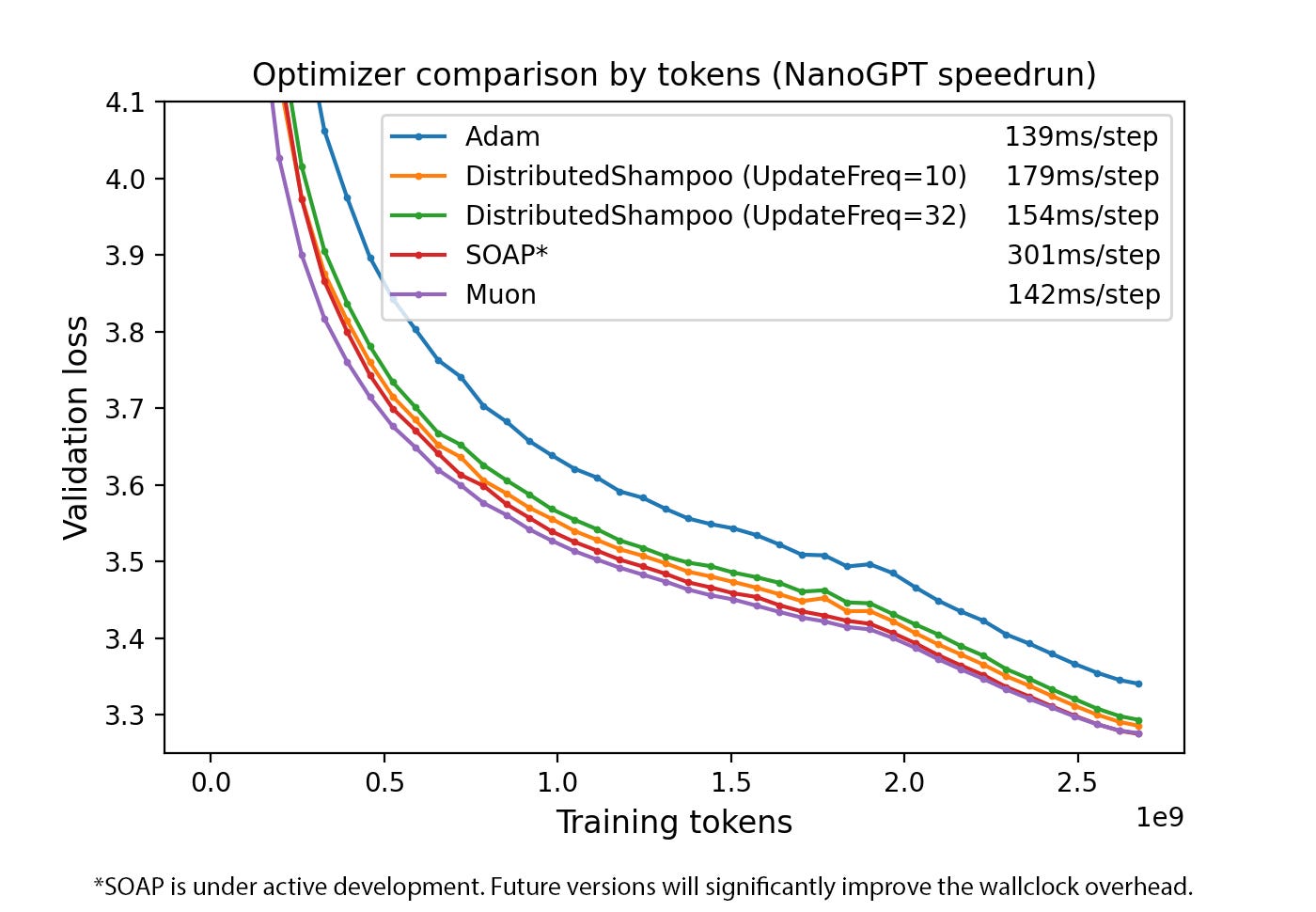
🧑🎓 Deep Dive: Understanding Muon optimizer
Training heavy transformers finishes sooner with Muon because gradients stop looping on same axes.
X saw a major weekend debate about Optimizer, and Muon led the discussion.
Muon was just a blog post. It got the author into OpenAI, and now he might be training GPT-5 with it now.
So lets’s really try to know Muon.
The landscape of deep learning optimization has long been dominated by adaptive first-order methods, most notably Adam and its variants. However, the relentless pursuit of training efficiency for ever-larger models has spurred the development of new algorithms that challenge this paradigm. Among the most prominent of these is the Muon optimizer, a method that has demonstrated remarkable performance in competitive, real-world training scenarios.
You can read the original author blog here.
Defining Muon: Momentum Orthogonalized by Newton-Schulz
Muon is an optimizer explicitly designed for the hidden layers of neural networks, targeting the 2D weight matrices that constitute the bulk of a model's parameters. Its name, an acronym for
⚙️ The Core Concepts
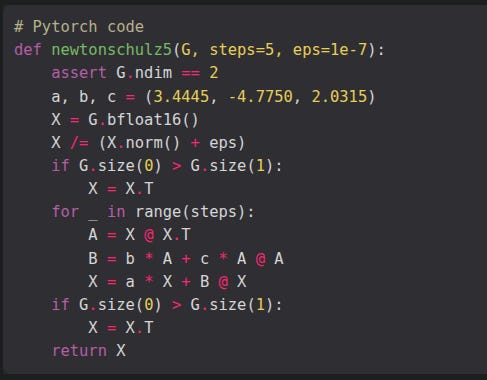
Muon updates the hidden-layer weight matrices only. A momentum buffer gathers recent gradients. The buffer then passes through a five-step Newton-Schulz routine that turns it into an almost-orthogonal matrix. That matrix, not the raw momentum, nudges the parameters.
where ‘NewtonSchulz5’ is defined to be the following Newton-Schulz matrix iteration (Bernstein & Newhouse, 2024; Higham, 2008; Björck and Bowie, 1971; Kovarik, 1970):
A ready-to-use PyTorch implementation of Muon can be found here. An example usage in the current NanoGPT speedrun record can be found here.
The algorithm proceeds as follows for each training step
The muon optimizer initializes its momentum buffer B_0 to zero for each weight matrix before training starts.
At each iteration it computes the gradient G_t of the loss with respect to the current parameters to identify the steepest descent direction.
The algorithm then updates the momentum buffer B_t by multiplying the previous buffer by the momentum factor mu and adding the new gradient G_t, which smooths noisy updates and preserves consistent directions.
This momentum buffer holds a running average of past gradients, capturing which directions have reduced the loss most effectively over recent steps.
Instead of applying this averaged gradient directly, muon turns B_t into an almost orthogonal matrix O_t using five fast Newton-Schulz iterations.
Newton-Schulz iteration relies on repeated simple matrix multiplications to approximate the process of making a matrix orthogonal, avoiding expensive exact decompositions.
Enforcing near orthogonality prevents the update from focusing only on a few dominant directions and lets smaller but informative gradient components drive learning.
Orthogonality means two directions are at right angles so they share no overlap. And by making update steps nearly orthogonal, Muon treats each direction independently and stops large gradient directions from drowning out smaller but useful signals.
The optimizer then updates the parameters θ_t by subtracting the product of the learning rate η and the orthogonal update O_t, completing one training step.
Repeating these steps spreads learning effort across all dimensions of the weight space, which leads to faster and more stable convergence in deep networks.
🚀 Hardware Efficiency of Muon
Muon avoids the high computational cost of exact singular value decomposition by using Newton–Schulz iteration to approximate an orthogonal update. This approach runs entirely on tensor cores in mixed precision and adds less than 1 % extra floating-point operations per training step, delivering fast and efficient hardware performance.
Why exact SVD is too slow on GPUs: Singular value decomposition first reduces a matrix to bidiagonal form with an operation count on the order of m·n², then applies iterative methods on that bidiagonal matrix costing another n³ flops.
GPU SVD routines often fail to leverage specialized tensor-core units, leading to poor utilization and slower performance compared to matrix-multiply workloads.
How Newton–Schulz runs efficiently on tensor cores: Newton–Schulz replaces decomposition with a loop of simple matrix multiplications and additions that converge to an orthogonal matrix.
NVIDIA tensor cores deliver up to 125 TFLOPS in mixed precision by performing 4×4 matrix-multiply-accumulate per cycle, making them ideal for these fixed-size GEMMs (General Matrix to Matrix Multiplication).
Using bfloat16 inputs with float32 accumulation ensures both speed and sufficient precision for the iteration to converge
Why five Newton–Schulz steps add under 1 % flops: Each iteration requires two matrix multiplies plus a few matrix additions. Ten multiplies per update remain negligible against the hundreds of multiplies in a transformer’s forward and backward passes. This design keeps the extra compute cost below 1 % of total floating-point operations per training step.
📈 Scaling to Frontier Models: Real-World Achievements
Kimi.ai trained a 16 B MoE on 5.7 T tokens with Muon and used only 52 % of AdamW flops after adding weight-decay and per-shape scaling. In their tech-report they said “Scaling law experiments indicate that Muon achieves ∼ 2× computational efficiency compared to AdamW with compute optimal training.”
That’s a wrap for today, see you all tomorrow.









great post