Mixture of Parrots: Experts improve memorization more than reasoning
Very interesting revelations in this paper. 💡
Very interesting revelations in this paper. 💡
Mixture-of-Experts (MoE) trade reasoning power for memory efficiency in LLM architectures
More experts don't make LLMs smarter, just better at memorizing
🤔 Original Problem:
Mixture-of-Experts (MoE) architecture lets LLMs scale parameters with minimal computational cost. But we don't know the exact performance tradeoffs between MoEs and standard dense transformers.
🛠️ Solution in this Paper:
• Analyzed theoretical limits of MoEs in reasoning tasks using graph problems
• Proved certain graph problems can't be solved by any number of experts of specific width
• Showed same tasks are easily solved by slightly wider dense models
• Used communication-complexity lower bounds to prove single-layer MoE needs critical dimension
• Pre-trained series of MoEs and dense transformers on 65B tokens
• Evaluated on math and natural language benchmarks
💡 Key Insights:
• MoEs excel at memorization but struggle with reasoning
• Increasing experts helps world knowledge tasks but not reasoning tasks
• MoEs match dense model performance with fewer active parameters for memorization
• MoEs are not a "free lunch" - benefits depend heavily on task type
• Architectural choices should be guided by specific task requirements
📊 Results:
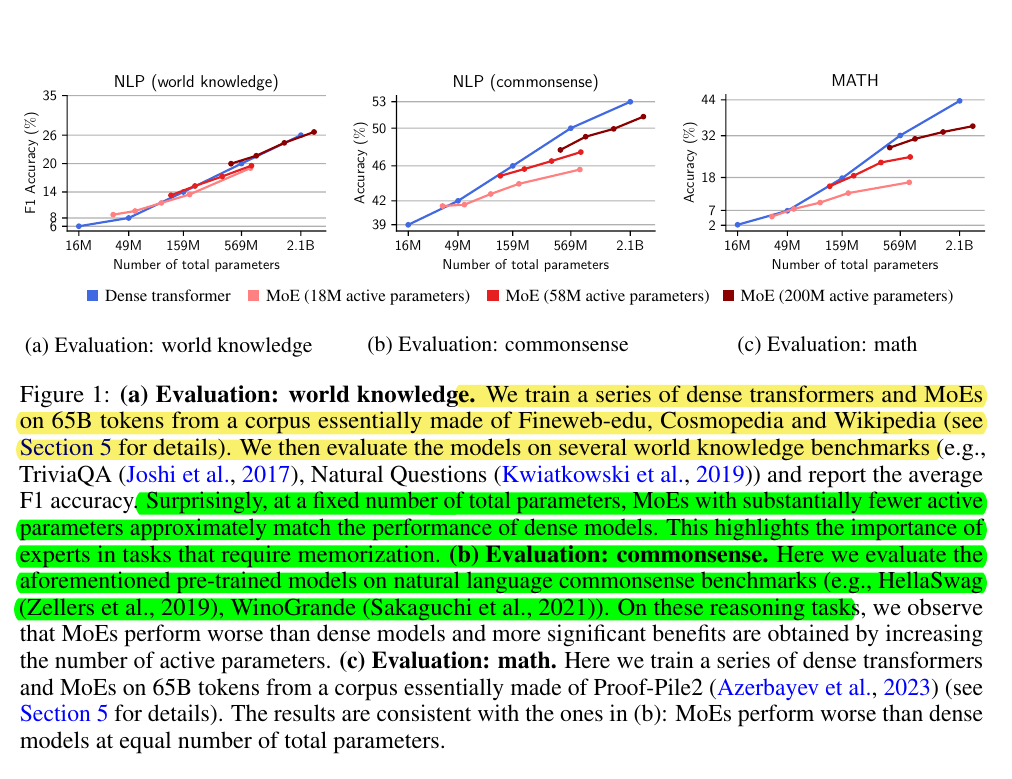
• On world knowledge tasks: MoEs matched dense performance with fewer active parameters
• On commonsense reasoning: MoEs performed worse than dense models at equal parameters
• On mathematical reasoning: Similar limitations as commonsense tasks
• Memory efficiency: MoE with 42M active parameters outperformed dense model with 10x parameters
📊 Findings
World knowledge tasks: MoEs matched dense model performance with fewer active parameters
Commonsense reasoning: MoEs performed worse than dense models at equal total parameters
Mathematical reasoning: MoEs showed similar limitations as in commonsense reasoning tasks
🧪 Theoretical evidence of limitations of MoEs in reasoning
The researchers proved that certain graph problems cannot be solved by any number of experts of a specific width, while these same tasks can be easily solved by slightly wider dense models.
They used communication-complexity lower bounds to show that a single-layer MoE requires a critical dimension to solve even simple graph connectivity problems.
🎯 Implications
So MoEs are not a "free lunch" solution - their benefits depend heavily on the task type.
They are highly effective for knowledge-intensive tasks but may not be the best choice for reasoning-intensive applications.
So architectural choices should be guided by the specific requirements of the target task.