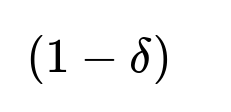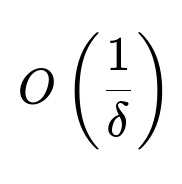ML Case-study Interview Question: Optimizing Recommendations for Learning Users via Two-Phase Multi-Armed Bandits
Browse all the ML Case-Studies here.
Case-Study question
A large e-commerce platform wants to design a recommendation system that personalizes items for a user who is also learning their own preferences over time. The platform frames this as a multi-armed bandit problem where each “arm” can represent an item or a higher-level category. The system only sees binary accept/reject outcomes from the user. The user simultaneously refines their internal utility estimates for each arm based on items they accept. The platform wants to identify which arm is truly the best for that user, knowing that the user might discard arms prematurely because of their own evolving preference estimates. How would you build a solution that can efficiently identify the best arm under these conditions, ensuring minimal rejections and a high probability of success?
Requirements:
Straight away propose a rigorous two-phase strategy that addresses:
Exploratory recommendations that are “safe,” helping the user gain more accurate internal estimates
A systematic approach to eliminating arms that the user decisively rejects
Why your approach outperforms standard bandit algorithms that assume stationary or black-box user preferences
How you would guarantee a confidence level in the final identified arm despite the user’s simultaneous learning
Detailed Solution
Problem Setup
The platform and the user interact sequentially. The system recommends an arm, the user accepts or rejects, and both update their estimates. Standard algorithms falter because they often ignore that the user’s preference evolves with each recommendation. The approach requires modeling user learning explicitly.
Two-Phase Approach
Phase-1 presents arms likely to be accepted, collecting acceptances to refine estimates while trying to avoid rejections. Phase-2 systematically eliminates arms once the user’s acceptance patterns show they are less favored.
Phase-1 (Sweeping)
The system recommends every arm at least once, but avoids arms that seem “risky” if early evidence suggests probable rejection. The total number of interactions here depends on how many acceptances are needed so the user’s internal estimates become more accurate. More interactions reduce the chance of misidentifying the best arm.
Phase-2 (Elimination)
The system recommends the arm with the least number of acceptances in prior interactions. Once an arm is rejected, it is removed. This continues until only one arm remains. That final arm is considered the user’s best choice.
Key Mathematical Guarantees
The research shows this two-phase method identifies the best arm with probability (1 - delta) after O(1/delta) interactions.
In these expressions, delta is the user-chosen error tolerance. The probability of successfully choosing the best arm is at least 1 - delta, and the number of interactions grows in proportion to 1/delta.
Why It Outperforms Standard Bandits
Traditional bandit approaches assume user rewards are fixed or drawn from static distributions. Here, the user’s accept/reject decisions shift as they learn their own utility. A strategy that factors in this ongoing user exploration (by limiting risky recommendations early and encouraging safe exploration) helps the user refine internal estimates more reliably, boosting final accuracy.
Practical Considerations
Implementation requires a mechanism to track how many acceptances each arm receives and to detect strong evidence that one arm’s upper confidence bound falls below another’s lower confidence bound. This can be done in a table or dictionary keyed by arm. Each time the user accepts an arm, both the user and system update confidence intervals. The approach also needs a stopping criterion for when to move from Phase-1 to Phase-2 based on acceptable false positive rates.
Example Pseudocode
class ArmRecord:
def __init__(self):
self.acceptances = 0
self.rejections = 0
def update_acceptance(self):
self.acceptances += 1
def update_rejection(self):
self.rejections += 1
# Phase-1
arms_data = {arm: ArmRecord() for arm in all_arms}
phase_one_interactions = some_predefined_number
for t in range(phase_one_interactions):
arm = choose_safe_arm(arms_data)
user_response = get_user_response(arm)
if user_response == "accept":
arms_data[arm].update_acceptance()
else:
arms_data[arm].update_rejection()
remove_arm_from_future(arms_data, arm)
# Phase-2
remaining_arms = list(arms_data.keys())
while len(remaining_arms) > 1:
arm_to_test = pick_arm_with_fewest_acceptances(remaining_arms, arms_data)
user_response = get_user_response(arm_to_test)
if user_response == "accept":
arms_data[arm_to_test].update_acceptance()
else:
remove_arm_from_future(arms_data, arm_to_test)
remaining_arms.remove(arm_to_test)
best_arm = remaining_arms[0]
Explanation in simple paragraphs: choose_safe_arm(arms_data) selects an arm with enough prior acceptances so the user is unlikely to reject it. remove_arm_from_future ensures no further recommendations for an arm the user rejects. In Phase-2, pick_arm_with_fewest_acceptances forces exploration of arms the user hasn’t confirmed thoroughly yet, accelerating elimination of inferior choices.
Final Confidence in the Identified Arm
Once only one arm remains, the system’s probability of correct identification is at least 1 - delta. The number of total trials scales with 1/delta, giving a flexible trade-off between precision and interaction cost.
Potential Follow-Up Questions
How do you choose the boundary between Phase-1 and Phase-2 in practice?
A threshold on total interactions in Phase-1 is often set by the acceptable error margin. A lower delta means more required acceptances, which leads to a longer Phase-1. If domain knowledge suggests user preferences remain uncertain until at least N acceptances, the system sets Phase-1 to about N interactions or more.
How would you adapt this approach if the user’s preferences drift over long timescales?
A rolling window or periodic reset of confidence intervals helps. The system discards outdated data after a certain horizon and re-enters Phase-1 if evidence suggests the user’s utility function changed. This is possible if rejections for the previously best arm spike unexpectedly.
Could we handle non-binary feedback signals?
Instead of accept/reject, the user might provide ratings. One can adjust the acceptance logic to a threshold-based rule. If the rating is above a chosen threshold, treat it as acceptance; otherwise, treat it as rejection. The main idea of ensuring safe exploration in Phase-1 and systematic elimination in Phase-2 remains.
Why does the user’s learning make a big difference compared to classical multi-armed bandits?
Classical algorithms assume a stationary reward distribution. Here, the “reward” from the user’s perspective changes as their internal preference model updates with each acceptance. The user might reject an arm early if they haven’t accumulated enough experience. Factoring in the user’s limited knowledge avoids unnecessary rejections and improves the final outcome.
How do you handle cold-start issues with new arms?
New arms need to enter Phase-1 in a controlled way. The system treats them as high-uncertainty arms that must be tried carefully. If the user quickly rejects them, they are removed. If the user accepts them enough times, they stay in the candidate pool for Phase-2.
What are the computational costs for large-scale arm sets?
The system must track confidence intervals and acceptance/rejection counts for each arm. Phase-1 might involve presenting each arm at least once. Phase-2 involves sorting or priority-queuing arms by acceptances. Methods that maintain an efficient data structure (like a min-heap for arms with the fewest acceptances) keep overhead manageable.
Could a different modeling of user rationality change the approach?
If the user isn’t purely rational and sometimes rejects arms by error, the algorithm can incorporate error tolerance or random noise in the acceptance model. The high-level two-phase design still holds, but there would be a correction step allowing re-check of arms previously rejected with uncertain confidence.
How would you test and validate this method pre-deployment?
Offline simulations with synthetic user models help tune the threshold and measure regret or incorrect identification rates. Online A/B tests compare the method against standard bandit baselines. The main success metric is how often the final recommended arm aligns with the user’s true best arm.
If you had to tailor your solution to extremely low interaction budgets, what modifications are needed?
Focus on rapid elimination. In Phase-1, the system might recommend only the arms most likely to be the best, using minimal random exploration. This reduces total interactions but risks discarding a hidden best arm. A well-chosen exploration-exploitation trade-off parameter determines how many arms to test under a tight interaction limit.