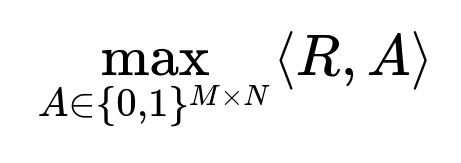ML Case-study Interview Question: Optimizing Personalized Rideshare Offers for Maximum Incremental Rides Within Budget
Browse all the ML Case-Studies here.
Case-Study question
A major rideshare platform wants to address an anticipated surplus of drivers by increasing passenger demand next week. They have a set of marketing offers (coupons, ride passes, or other incentives) and a wide pool of passenger segments with different behaviors. They also have a fixed budget. Formulate a personalized campaign strategy to decide which offer goes to which segment to maximize incremental rides while meeting budget targets and controlling variance. How would you approach the problem, estimate incremental rides, measure cost, manage uncertainty, and maintain continuous learning?
Proposed Solution
Personalized marketing aims to maximize incremental rides while respecting budget constraints and reducing variance around the final outcome. The process begins with defining key metrics and gathering necessary data on passenger behavior and past responses to similar incentives.
Defining Key Metrics and Modeling Incrementality
Incremental rides capture the difference between the number of rides a segment would take with an offer versus without that offer. Observing the true incrementality requires modeling or experimentation, because we rarely see both scenarios (offer vs. no-offer) for the same set of passengers at the same time. Data is gathered via randomized tests where certain segments receive specific offers, and others do not. Machine learning models (tree-based or neural networks) then predict incremental rides and cost for each segment-offer combination.
Core Optimization Framework
To illustrate the main optimization goal, consider a matrix R of incremental rides predictions and a matrix C of associated costs. A is a matrix of binary decisions indicating whether a specific segment receives a particular offer. The objective is:
Where:
R is the matrix of predicted incremental rides for each segment-offer combination.
A is the decision matrix (1 if the segment gets the offer, 0 otherwise).
M is the number of segments.
N is the number of offers.
The expression < R, A > represents the sum of element-wise products R_{ij} * A_{ij}.
A budget constraint applies similarly:
Where C is the matrix of predicted costs for each segment-offer pair, and < C, A > is the total cost incurred. The optimization program can also incorporate a variance penalty to reduce uncertainty.
Handling Variance
Estimates of incremental rides and costs are probabilistic. Passenger behavior fluctuates for many reasons, so a purely deterministic approach might lead to unpredictable results. To manage risk, the optimization can include a variance-controlling term or chance constraints that relax strict budget and volume targets in exchange for reduced variance. This approach sacrifices some average efficiency to avoid large deviations from the budget or expected rides.
Maintaining Continuous Learning
User behavior evolves, so retraining and refreshing are mandatory. Relying on outdated data leads to incorrect predictions and wasted budget. A robust data pipeline logs each campaign’s results, combining explore/exploit strategies to update models. This cycle ensures models remain accurate and adaptive.
Example Code Snippet (High-Level)
import numpy as np
from scipy.optimize import linprog
# R: incremental rides matrix (M x N)
# C: cost matrix (M x N)
# budget: total available budget
# Flatten the matrices for linear programming
R_flat = R.flatten()
C_flat = C.flatten()
# We want to maximize incremental rides -> minimize negative rides
obj = -1 * R_flat
# Build constraints:
# 1) cost <= budget
A_ub = [C_flat.tolist()]
b_ub = [budget]
# 2) A must be binary => handle via integer programming or define bounds in real scenario
bounds = [(0, 1) for _ in range(len(R_flat))]
# Solve (this is a simplified approach)
res = linprog(obj, A_ub=A_ub, b_ub=b_ub, bounds=bounds, method='highs')
# Convert result back to matrix form
A_opt = res.x.reshape(R.shape)
This sketch shows a simplified linear programming approach ignoring variance considerations and binary constraints. In practice, integer programming or specialized solvers handle binary decision variables and variance adjustments.
How would you address data-sparsity issues for rare passenger segments?
Small or rare segments might appear infrequently in historical data, making it hard to predict behavior. Aggregation strategies group them into larger segments based on similar features. Bayesian approaches can pool prior information, shrinking extreme estimates toward overall averages. Techniques like regularization or hierarchical modeling are also useful. These methods ensure the model is not overfitting small samples and can generalize predictions.
How do you measure the true incremental effect when randomization is not always possible?
When fully random experiments are limited, comparison groups or counterfactual modeling are used. Techniques like propensity score matching approximate random assignment by creating balanced comparison sets. Another approach is difference-in-differences, which compares changes in outcomes before and after a campaign across treated and untreated segments. Logging small randomized samples over time is also crucial to keep an unbiased control for assessing incrementality.
How do you incorporate variance constraints within an optimization solver?
Variance constraints involve the distributions of predicted metrics. Some methods add a term like λ * Var(cost) or λ * Var(incremental_rides) to the objective. Others use chance constraints, which specify that the probability of exceeding the budget must be below a certain threshold. For large-scale problems, approximate algorithms or sample-based approaches (like sample average approximation) estimate the distribution by drawing multiple samples from the predictive models. Each sample yields a scenario that feeds into a scenario-based optimization, capturing random fluctuations.
How would you handle interference effects, where sending offers might shift marketplace dynamics?
Substantial offer-driven demand changes can lead to price surges or driver supply imbalances, which distort cost and ride estimates. One way is to simulate or model the market equilibrium. Another is to monitor system-level signals (driver wait times, ride completion times) to adjust offers in real-time. For large-scale campaigns, A/B tests with region-level or time-sliced randomization measure whether sending more offers in a certain area inflates driver earnings or wait times. Incorporating these system-wide effects into the optimization ensures more accurate, stable outcomes.
How do you maintain fairness or compliance when deciding which segments receive offers?
Any selection mechanism must be analyzed for bias. Automated personalization can inadvertently exclude certain groups. Fairness constraints can enforce equal opportunity or demographic parity. Compliance guidelines might require consistent communication or benefits across different demographic categories. Including demographic features with regularization or constraints that ensure fairness-based metrics (like equalized odds) remain within thresholds can limit bias. This often entails re-weighting or adjusting the final optimization solution to meet policy requirements.
How do you sustain model performance despite changes in passenger behavior over time?
User habits shift due to seasonality, economic fluctuations, or external events. Implement continuous model updates and monitor key metrics (e.g., root mean squared error for cost predictions, incremental rides consistency). If drift is detected, reevaluate the pipeline. Use online learning methods that update parameters incrementally as new data arrives. Schedule model retraining or re-tune hyperparameters at regular intervals or upon detecting significant data distribution changes.
What if your budget overshoots or undershoots mid-campaign?
Implement real-time or near real-time feedback loops. If spending is close to the cap, throttle the most expensive offers first or optimize for cheaper segments. If there is unspent budget and remaining time, expand the campaign to additional segments or upgrade smaller incentives. Re-running a dynamic optimization ensures resources are allocated efficiently based on the latest performance signals.
How do you handle leadership concerns about trusting black-box ML models?
Present robust offline metrics and run pilot experiments in controlled environments. Provide interpretability reports (e.g., using SHAP or LIME) to highlight key drivers behind predictions. Keep transparency about model assumptions, limitations, and error bounds. Show that the campaign logic is consistent with established domain insights. Compare model outputs against simpler baselines or rules to build trust.
What techniques would you use to reduce targeting bias and explore new segments?
Use distribution matching to re-weight or select new participants in each wave of experimentation. Adopt exploration policies that randomly try small subsets of segments to gather fresh responses. Over time, incorporate these new data points into the main model so it remains robust to unseen regions of the feature space. Implement a structured multi-armed bandit or contextual bandit that balances exploitation of known effective offers with exploration of untested segments.
How can the optimization approach be extended beyond simple coupon-based incentives?
Incorporate experience-based offers (premium rides, faster pickups) by defining cost and incremental ride estimates for these new incentives. If additional marketplace data suggests strong synergy between certain offers and specific passenger behaviors, expand the model to handle these multiple objective parameters. Evaluate net profit or long-term retention as alternative objectives. The same underlying principles of incremental measurement, cost prediction, optimization, and variance control still apply.