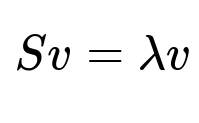ML Case-study Interview Question: PCA Eigenvalue Clipping & Clustering for Explainable Fraud Feature Selection
Browse all the ML Case-Studies here.
Case-Study question
You have a large dataset with several thousand features for a fraud detection system. The data distribution changes over time, but the correlation structure of the features remains mostly stable. You suspect model overfitting because of the high number of features. The business demands that you keep original feature explainability. How would you design a feature selection approach that filters out noisy features while still preserving the most meaningful and diverse information?
Detailed solution
Background on overfitting and feature redundancy
Overfitting increases when the model has too many features, especially if many are correlated or carry little unique information. Large models also become expensive to maintain. Reducing features helps generalize better, lowers infrastructure costs, and keeps the model easier to debug.
Covariance structure and PCA overview
Principal Component Analysis (PCA) finds directions in feature space (eigenvectors) that capture maximal variance. These directions often reveal how features correlate. PCA solves the eigenvalue problem for the covariance matrix S. The core condition is:
Here, S is the covariance matrix of the features, v is the eigenvector, and lambda is the corresponding eigenvalue. Bigger eigenvalues usually represent stronger correlations that might hold important signals.
Noise in eigenvalues and eigenvalue clipping
Real-world data can inflate eigenvalues in random ways. Many eigenvectors actually correspond to noise. Eigenvalue clipping removes these spurious components by comparing the original set of eigenvalues with the distribution of eigenvalues computed on a shuffled version of the same dataset. Shuffling each feature independently breaks all real correlations, giving a pure noise spectrum. Any eigenvalue that lies outside that noise distribution is retained as signal.
Building a filter operator and reconstructing the dataset
Keep only the eigenvectors v that correspond to clipped (signal) eigenvalues. Construct a filter operator F that projects the data onto those signal eigenvectors and then back to the original space. This removes noise-induced components while keeping original feature dimensions. Let D be your original data. Then F(D) is the cleaned version of D. The decomposition is D = F(D) + N(D), where N(D) is the noisy part.
Clustering features in the filtered dataset
Compute the correlation matrix of F(D). Define a distance measure d = 1 - |S|, where S is the correlation. This distance gets small when two features correlate strongly. Perform hierarchical clustering on that distance matrix to group together features that share the same underlying signal. A cluster of features is largely redundant. You can discard many within each cluster and keep one or two that best preserve interpretability.
Practical impact
This approach cuts away redundant signals and improves generalization. Tests showed that removing 70% of features led to a 20% improvement in fraud detection performance. Model size also shrank, saving infrastructure costs and speeding up deployment.
Example Python snippet
import numpy as np
from sklearn.decomposition import PCA
# Suppose data is in a NumPy array called data with shape (n_samples, n_features).
# Step 1: Shuffle features to estimate noise eigenvalues
shuffled_data = data.copy()
for j in range(data.shape[1]):
np.random.shuffle(shuffled_data[:, j])
# Step 2: Fit PCA to original data
pca_original = PCA()
pca_original.fit(data)
eigenvalues_original = pca_original.explained_variance_
# Step 3: Fit PCA to shuffled data
pca_shuffled = PCA()
pca_shuffled.fit(shuffled_data)
eigenvalues_shuffled = pca_shuffled.explained_variance_
# Compare histograms or distributions to find clipped threshold
# (Implementation detail depends on domain heuristics)
# Step 4: Filter operator using the signal eigenvectors
# Suppose we keep signal_indices that lie above the clipping threshold
signal_indices = [i for i in range(len(eigenvalues_original)) if ...] # your criterion
signal_eigenvectors = pca_original.components_[signal_indices, :]
# Reconstruct data from signal only
# transform() -> project onto signal subspace
# inverse_transform() -> map back to original space
clean_data = np.dot(np.dot(data, signal_eigenvectors.T), signal_eigenvectors)
The main idea is to reconstruct only from eigenvectors you trust as genuine signal. Then you cluster correlated features in clean_data and pick representatives from each cluster.
Follow-up question 1
How do you handle the possibility that the data distribution is not strictly normal, making the Marchenko-Pastur assumption invalid?
Answer
Normal assumptions break down in many real datasets. Instead of relying on the analytic form of the Marchenko-Pastur distribution, shuffle each feature to simulate a noise-only dataset. That preserves individual feature distributions but destroys cross-feature correlations. Eigenvalues from this noise dataset approximate the noise spectrum. Any true correlation should push the original eigenvalues beyond that noise range.
Follow-up question 2
Why not just keep the top principal components using the elbow method?
Answer
The elbow method keeps the components that explain most of the total variance. It does not separate genuine correlation from noise. A large eigenvalue might still be contaminated. Eigenvalue clipping explicitly measures how far an eigenvalue stands from what pure noise would generate. This method isolates real signal instead of assuming all variance is useful.
Follow-up question 3
Explain why we still preserve original feature names and interpretability even though PCA was used.
Answer
We only use PCA to identify noise eigenvectors and then build a filter operator. We map data back to its original feature space, so each dimension corresponds to an original feature. We never replace features with principal components. We only remove the noise component within each feature, keeping the interpretability.
Follow-up question 4
How do you decide the number of clusters after filtering?
Answer
Each retained eigenvector effectively adds a distinct correlation pattern. Retaining s signal eigenvalues suggests s major correlation directions. This translates into s clusters in the filtered correlation matrix. A hierarchical clustering algorithm naturally reveals that many features collapse into a cluster for each direction. Final cluster counts match the count of retained eigenvalues.
Follow-up question 5
How can this approach improve predictive performance?
Answer
It removes irrelevant or redundant dimensions that often carry only noise. Noise can inflate variance and distort model coefficients, leading to overfitting. Focusing on signal-bearing features strengthens generalization. Empirical results show a consistent drop in error when these clipped features feed a fraud model.
Follow-up question 6
What implementation details matter most for large-scale production?
Answer
Efficient computation of the covariance matrix and PCA is critical with high-dimensional data. Incremental or randomized PCA can help. Shuffling in place requires memory considerations when data is very large. Also consider a distributed or parallel approach for hierarchical clustering. Avoid scanning the entire dataset if sampling can approximate correlations well.
Follow-up question 7
How would you validate that this feature selection technique genuinely improves over simpler methods?
Answer
Compare final model performance using standard metrics like AUC or recall on a separate test set. Track changes in training time, inference latency, and maintenance cost. Check if interpretability remains acceptable to stakeholders. Evaluate stability across multiple runs or time windows to confirm consistent gains.