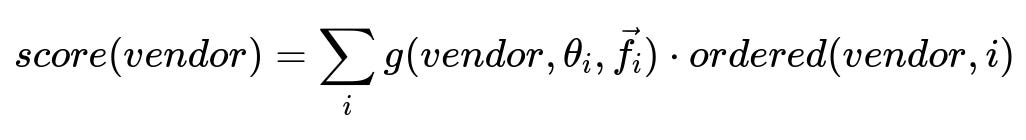ML Case-study Interview Question: Scalable Personalized Vendor Ranking via Matrix Factorization and User Similarity

Browse all the ML Case-Studies here.

Case-Study question

You are given a large-scale online ordering platform that connects millions of customers with thousands of vendors. The task is to build a personalised recommendation system that ranks vendors for each customer based on explicit and implicit feedback. The recommendation system should leverage ordering history, ratings, vegetarian vs non-vegetarian preferences, and other relevant features. How would you design such a system to improve conversion rates and user satisfaction while scaling to accommodate new features and millions of daily interactions?

Detailed Solution

A starting approach uses a similarity-based model that treats each customer as a vector of features (for instance, the number of orders and a vegetarian score). Computing the angle between two vectors helps measure closeness through cosine similarity. Customers with similar vectors should have similar preferences. One then computes a vendor score for a given customer by summing over vendors that these similar customers have ordered from, weighted by the similarity function.

The summation is over comparable customers i. The function g maps the vendor, the angle theta_i between the target customer’s feature vector and customer i’s feature vector, plus any extra features f_i, to a similarity-based weight. The term ordered(vendor,i) indicates whether customer i actually ordered from that vendor. This yields a score for every vendor in the catalog, then ranks vendors in descending order of that score.

This technique produces interpretable outputs because you can see which similar customers influenced the final ranking. It struggles to scale for large sets of customers and many features, because each vendor score depends on a summation over many other customers. It also requires careful handling of dietary constraints. For instance, if a vegetarian customer is considered similar to a non-vegetarian, naive sharing of vendors could produce irrelevant or negative recommendations.

An alternative approach uses collaborative filtering via matrix factorization. A matrix M of size (number_of_customers x number_of_vendors) encodes interactions: the (customer, vendor) entry might be 1 if ordered, and 0 if not. This matrix can be factorized into low-dimensional embeddings, where M ~ P x Q^T, with P capturing customer embeddings and Q capturing vendor embeddings. Multiplying P and Q^T produces a predicted score for every (customer, vendor) pair. This factorization has high training efficiency, handles large volumes of data, and can incorporate side information by injecting additional features (for instance, vegetarian constraints or rating signals) into the interaction matrix. The resulting embeddings can also be reused in other models across the platform.

The platform might then post-process the final ranking with business rules. This can address situations like brand promotions, vendor reliability, or regulatory constraints. Even though the raw model might rank certain vendors highly, the system can reorder or remove certain vendors based on these rules.

Below is an illustrative Python snippet showing a simplified approach to a user-based similarity system using basic cosine similarity and user histories. This example uses dictionaries to represent user orders:

import numpy as np

def cosine_similarity(vec_a, vec_b):
    dot_product = np.dot(vec_a, vec_b)
    norm_a = np.linalg.norm(vec_a)
    norm_b = np.linalg.norm(vec_b)
    if norm_a == 0 or norm_b == 0:
        return 0
    return dot_product / (norm_a * norm_b)

# Suppose user_profiles is a dict: user -> feature_vector
# Suppose user_orders is a dict: user -> set_of_vendors

def recommend_vendors(target_user, user_profiles, user_orders):
    target_vector = user_profiles[target_user]
    scores = {}
    for other_user, other_vector in user_profiles.items():
        if other_user == target_user:
            continue
        similarity = cosine_similarity(target_vector, other_vector)
        for vendor in user_orders[other_user]:
            scores[vendor] = scores.get(vendor, 0) + similarity
    recommended = sorted(scores, key=scores.get, reverse=True)
    return recommended

target = "Alice"
ranked_vendors = recommend_vendors(target, user_profiles, user_orders)
print(ranked_vendors)

This code finds similar customers to "Alice" by cosine similarity and sums their similarity weights for each vendor. In practice, one would filter out vendors that violate constraints, factor in the number of orders instead of a binary set, and incorporate more sophisticated weighting or partial feedback signals.

How to Handle Follow-up Questions

How would you address new or rarely used vendors (cold start)?

In matrix factorization, new vendors have no established history. One approach is to initialize vendor embeddings with population averages or side features like cuisine type or location. Another approach is to run a content-based filter that uses vendor metadata (e.g., category, price range, and dietary tags) to produce initial recommendations until enough user interactions accumulate for the model.

How would you handle new users (cold start)?

The system can show popular or trending vendors that align with known demographic or contextual data if explicit signals are absent. The system can prompt for minimal user preferences (for example, vegetarian vs. non-vegetarian) to refine the initial set of vendors. Over time, the user’s explicit or implicit actions refine the embedding or similarity profile.

How do you incorporate time or recency of orders?

A weighting scheme that applies higher importance to recent orders can mitigate stale recommendations. One can multiply each interaction by a decay factor that diminishes as time passes. In matrix factorization, one can store time-based features in the interaction matrix or maintain a short-term embedding for recency.

How would you scale this to millions of customers?

Matrix factorization is computationally efficient at large scale. Factorization-based methods can leverage distributed computing frameworks. Embeddings can be trained incrementally with streaming updates. For user-based similarity, approximate nearest-neighbor (ANN) search techniques help by clustering users into relevant groups, instead of a full user-to-user comparison.

How do you evaluate performance?

Offline evaluation uses metrics like mean average precision (MAP), Normalized Discounted Cumulative Gain (NDCG), or recall at top-k. Online evaluation via A/B tests measures impacts on conversion rates, order volume, or user retention. One must ensure the chosen metric aligns with the platform’s business objectives and that it captures the user’s satisfaction accurately.

---