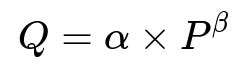ML Case-study Interview Question: Optimizing Fashion Markdowns: A Hybrid ML Approach Using Price Elasticity Modeling.

Case-Study question

You are tasked with designing and deploying a machine learning system to optimize promotional pricing for a large online fashion retailer. The retailer stocks more than 100K items, with limited seasonality windows and fast-changing trends. The challenge is to decide optimal markdowns to sell out the right stock at the best possible profit margins, while dealing with partial information about pricing outcomes. Propose a detailed system architecture and machine learning solution that addresses demand modeling, profit optimization, offline validation, and online testing. Explain your approach clearly, with emphasis on:

• Managing unknown price-demand relationships

• Balancing cold-start scenarios versus fully data-driven price optimization

• Ensuring financial risk control and alignment with business metrics

• Designing rigorous offline and online evaluation to confirm uplift over manual or rule-based markdown strategies

Present concrete solution steps and any relevant mathematical formulations.

Detailed Solution Explanation

Efficient markdown management requires two phases: a cold-start solution for new or rarely discounted products, and a fully trained approach once you have sufficient sales-history data. Cold-start helps you control revenue and profit risk. A fully trained solution uses predicted price elasticity to maximize profit.

Cold-Start Strategy (System A)

System A uses no historical demand modeling. It assigns markdowns to products based on supply-side constraints such as remaining stock value and desired profit margin. The method ensures the total discounted value of items remains within preset revenue targets. System A is powerful when data is sparse or nonexistent for new styles.

The algorithm applies an iterative search to locate a set of products and prices that achieve two objectives:

1. Sell through all identified stock

2. Respect financial constraints, such as a required margin threshold

System A is straightforward to deploy because it needs minimal demand data. The outcome is that new or low-data products contribute data for subsequent modeling.

Fully Trained Model (System B)

System B incorporates price elasticity modeling, partial-information training, and real-world validation.

Price elasticity quantifies how demand changes when price changes. A simple elasticity model might relate daily demand Q to price P via power-law or exponential forms. One example:

Where Q is demand, P is price, alpha is a learned intercept term, and beta is the elasticity parameter that captures how sensitive demand is to price changes. A negative beta means higher price reduces demand, which usually applies in fashion e-commerce.

Below this formula, demand is predicted across different price points. The system then selects the price that maximizes projected revenue or profit.

Partial information complicates demand estimation because you only see data at historically chosen prices. A thorough offline validation protocol is crucial to produce unbiased estimates. This involves splitting data by time or product categories, ensuring the model doesn’t learn only from previously favored price ranges.

To reduce risk of inaccurate elasticity estimates, the system uses constraints derived from offline validation. For instance, if the elasticity uncertainty is large for a particular item, the system picks a safer markdown.

Rigorous Offline and Online Testing

Offline tests measure how well predicted sales match observed sales on held-out data, but partial-information limitations mean you must consider the price range covered in your training. True confirmation requires randomized online tests, where a fraction of products receive model-driven markdowns and the remainder follow existing manual or rule-based methods. System performance is measured via actual revenue and profit lift.

The combined approach of cold-start (System A) plus elasticity-based optimization (System B) often yields significant improvements in profitability over traditional operations. System A is deployed when data is scarce to manage risk. System B is used after enough data is gathered. Both systems can run in parallel, feeding data to each other.

Example Code Snippet in Python

Below is a simplified version illustrating how you might structure price elasticity model training. This code uses a scikit-learn-style regression approach.

import numpy as np
from sklearn.linear_model import LinearRegression

# Suppose we log-transform Q and P for a simple linear fit
# log(Q) = log(alpha) + beta * log(P)

def train_elasticity_model(prices, demands):
    # prices and demands are numpy arrays
    # we exclude zero or negative demands to avoid log(0)
    valid_indices = (demands > 0) & (prices > 0)
    x = np.log(prices[valid_indices]).reshape(-1, 1)
    y = np.log(demands[valid_indices])
    model = LinearRegression()
    model.fit(x, y)
    alpha = np.exp(model.intercept_)
    beta = model.coef_[0]
    return alpha, beta

def predict_demand(p, alpha, beta):
    return alpha * (p ** beta)

prices_train = np.array([10, 12, 15, 20])
demands_train = np.array([100, 80, 50, 30])

alpha_est, beta_est = train_elasticity_model(prices_train, demands_train)

test_price = 14
predicted_demand = predict_demand(test_price, alpha_est, beta_est)
print("Test price:", test_price)
print("Predicted demand:", predicted_demand)

This example demonstrates how you might estimate alpha and beta from historical data. In a real system, more complex models can incorporate seasonality, category interactions, and partial-information corrections.

Potential Follow-Up Questions

1) How do you address the partial-information problem in your training data?

You hold out a portion of historical data in a way that preserves the distribution of prices for certain products. You avoid letting the model see future price points or price points artificially introduced by manual pricing. You set up time-based splits and carefully track the historical price policies. This ensures each product’s unseen price variations are not leaking into training. Techniques such as inverse propensity scoring and doubly robust estimation help correct for biases introduced by non-random historical markdowns.

In practical terms, you partition the data by time, so the model sees only older data in training, then you check performance on newer data with known outcomes. You sometimes apply matched product groupings to approximate the randomized design you would prefer in an ideal scenario.

2) How do you choose the objective when optimizing price?

You define a target function that captures total profit or revenue. If profit is the priority, you include cost-of-goods-sold in your equation so that predicted profit = (Price - UnitCost) * Demand. The system picks the price that yields the highest expected profit.

Another approach focuses on revenue or units sold, depending on business strategy. Profit-oriented solutions often provide the best margin. But certain contexts might require clearing stock quickly or building brand awareness, so the objective might vary.

3) How can you ensure that the cold-start system does not discount too aggressively?

System A has explicit bounds on allowed total stock value. It iteratively narrows down product sets and discount levels, pausing once you reach your required financial limit. This approach ensures you don’t over-discount. It systematically re-checks the ratio of discounted value to full-price value, adjusting sets until your margin objectives remain in range. It also leverages up-to-date stock levels, so excessive markdown only occurs when absolutely necessary.

4) How do you deal with uncertainty in estimated price elasticity?

You measure predictive uncertainty by looking at residual errors and confidence intervals from the price elasticity model. You might add a margin of safety around the elasticity parameter. If the confidence interval suggests a broad range of possible betas, the system picks a price less extreme than a point estimate. You can also incorporate Bayesian or quantile regression methods to handle this systematically.

5) How do you justify deploying these solutions versus manual or rule-based approaches?

Quantitative tests in randomized trials show improved profit or margin when the machine learning solution is used. You compare system-driven pricing against an established manual method across a representative subset of products. Statistically significant improvements in realized margin and sell-through confirm the benefit. These results must align with any operational constraints, such as brand identity and discount frequency. Once proven, you scale the system to all products.

6) How do you handle data quality issues like missing or noisy sales data?

You implement data pipelines that enforce checks for anomalies, out-of-range values, or product merges. Missing data might be imputed using short-term historical trends or category-level averages. You track data integrity continuously. The system avoids making optimization decisions on highly uncertain data. It may revert to safer, more conservative markdown levels if product data is unreliable.

7) What is your approach for updating the model over time?

You adopt a rolling retraining schedule. You re-train weekly or monthly, incorporating the newest data, including any novel price actions introduced by the system itself. This feedback loop updates elasticity estimates, ensuring the model remains aligned with shifting trends. You monitor performance metrics to detect when retraining is necessary. If there are large external shifts, such as sudden changes in consumer behavior, you re-train immediately or revert to cold-start logic until new data stabilizes.

8) Is there a risk that the model could learn to set prices too high and hurt sales?

Yes. Overly high prices might maximize short-term profit per unit but reduce total sell-through. That leads to leftover inventory. Including a term in the objective that penalizes leftover stock or an explicit constraint on inventory ensures the system remains balanced. You can also track how the model’s recommended prices compare to operationally acceptable thresholds. Frequent re-training adjusts for shifting consumer behavior. Real-time business rules can act as guardrails to prevent brand-damaging price spikes.

9) How would you incorporate multi-objective optimization, like balancing both revenue and sustainability goals?

You define each goal quantitatively. For sustainability, you might penalize large leftover stock or excessive returns. You embed these penalties in the optimization function or treat them as constraints. The system might solve a combined objective that weighs each component. Techniques like Pareto optimization or weighted sum approaches handle multi-objective tradeoffs. You test solutions offline to find an acceptable tradeoff curve before deploying.

10) Why is the online experiment so critical?

Offline metrics can be misleading if your training data lacks sufficient price exploration. Only a live randomized test can confirm actual customer response to new price points. This real-world measurement is essential to validate that your elasticity estimates and optimization steps translate to genuine revenue or profit lift. It also exposes unintended side effects, such as user dissatisfaction with extreme discounts or suboptimal brand impact.

These answers illustrate how to design, validate, and deploy a markdown optimization system that outperforms manual rule-based approaches. The careful combination of cold-start logic for risky scenarios and a full price-elasticity framework for data-rich scenarios can substantially improve profit margins while aligning with the retailer’s high-level objectives.

---