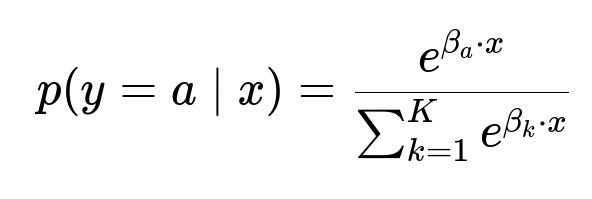ML Case-study Interview Question: ML Payment Routing: Boosting Renewals with Inverse Probability Weighting
Browse all the ML Case-Studies here.
Case-Study question
A growing subscription-based platform faces recurring payment renewals across multiple gateways. The platform uses a rule-based routing engine, splitting transactions among gateways at fixed ratios. This static system fails to adapt to changing approval rates, causing suboptimal performance. The platform wants a machine learning-based routing engine that improves renewal success rates and reduces unintentional cancellations. How would you, as a Senior Data Scientist, design and implement this system at scale?
Detailed solution approach
A supervised learning framework can replace the rule-based routing. A multi-class classification model can predict the best gateway for each transaction. Historical data from the existing routing logic (with transaction outcomes) becomes the training source. A key challenge is the inherent imbalance introduced by the old routing ratios. A gateway receiving fewer transactions might appear to have an inflated or deflated success rate, making direct training biased. Inverse probability weighting addresses this issue by assigning weights inversely proportional to the probability of each gateway being chosen under the old rules.
w_{i} is the weight for the i-th transaction. p(a_{i} | x_{i}) is the probability that the rule-based system routed transaction i to gateway a_{i} given features x_{i}.
Sampling the data with these weights ensures balanced training for each gateway. The model thus learns a realistic estimate of each gateway’s success probability for given features (such as transaction type, product type, and card type).
The resulting dataset can be used to train a multi-class logistic regression:
p(y=a | x) is the predicted probability that gateway a is the best choice for features x. K is the number of possible gateways. x represents the feature vector. beta_{a} is the coefficient vector for gateway a.
The model output is a set of predicted success probabilities for all gateways. Picking the gateway with the highest probability serves as the routing decision. Deployment involves exposing the trained model via an internal service. Engineers integrate it with the routing engine to direct subscription transactions in real time.
A periodic model refresh is crucial because gateway performance can shift over time. Stale models might overfit past gateway behavior. Retraining on recent data ensures the routing engine adapts to changing approval rates. After deployment, an A/B test (comparing the old system vs. the new one) measures approval rate lift. Significant improvements confirm that the system reduces payment failures.
A short Python snippet for a simplified training pipeline:
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
data = pd.read_csv("payment_data.csv")
# Suppose 'gateway_chosen' is the gateway label under old rules.
# 'success' is 1 if transaction succeeded, else 0.
# 'features' includes columns for transaction, product, card types, etc.
# Compute routing probability p(a_i|x_i) from old rules (stored or inferred).
# Suppose 'routing_prob' is that probability for each record.
data['weight'] = 1.0 / data['routing_prob']
X = data[['feature1', 'feature2', 'feature3', 'feature4']]
y = data['gateway_chosen']
model = LogisticRegression(multi_class='multinomial', solver='lbfgs', max_iter=1000)
model.fit(X, y, sample_weight=data['weight'])
# For a new transaction:
# new_x is a feature vector for the new transaction
pred_prob = model.predict_proba([new_x])[0]
best_gateway = np.argmax(pred_prob)
This code trains a multi-class logistic regression with inverse probability weighting, then uses it to pick the gateway with the highest predicted probability.
Follow-up question 1: How do you handle scenarios where the underlying success rates for gateways shift over time?
Models degrade if real-world patterns diverge from training data. Frequent refresh and incremental learning can catch new trends. A shorter lookback window ensures the model sees recent data. Monitoring key metrics (approval lift, conversion rates) provides signals of drift. Low-latency logs let the model detect drops in gateway performance and re-train quickly. In production, a near-real-time system can adapt so that newly observed success rates are reflected in the next model update.
Follow-up question 2: Why inverse probability weighting rather than a naive supervised approach?
Naive training on old routing outcomes inherits heavy bias. Gateways with small traffic share have fewer success or failure samples, causing poor estimation. IPW corrects that bias by upweighting underrepresented samples. The re-sampled distribution approximates a scenario where all gateways had equal exploration. This gives a fairer view of each gateway’s true performance.
Follow-up question 3: Why not directly remove transactions from the gateway with poor performance?
Shutting off gateways with lower success rates might overlook dynamic changes. A gateway that performs poorly this month might improve next month. Disabling it completely means losing potential conversions. An adaptive system re-evaluates gateway performance regularly. Hard-coding permanent gateway eliminations leads to rigidity and can miss evolving market conditions and gateway improvements.
Follow-up question 4: How would multi-armed bandits or a reinforcement learning approach differ?
A supervised approach trains on historical labeled data. A multi-armed bandit or reinforcement learning framework treats gateway selection as a sequential decision problem. The model starts with partial knowledge and explores different gateways. The system updates its policy after observing live feedback (success or failure). Non-stationary bandit algorithms handle changing approval rates with minimal retraining, adjusting the exploration-exploitation trade-off in real time. A purely supervised approach typically relies on periodic batch updates. A bandit or RL-based system can adapt more fluidly to short-term fluctuations in gateway performance.
Follow-up question 5: How would you introduce additional cost constraints?
Charging fees, transaction costs, or penalty fees from gateways might matter. A cost-aware objective can incorporate these terms. A suitable approach is training the model to optimize for net profit or net approval, factoring both success probabilities and gateway fees. A custom cost function can penalize expensive gateways if their higher approval rates do not offset the overhead. A constrained optimization approach or a weighted loss function might balance cost vs. success rates during training.