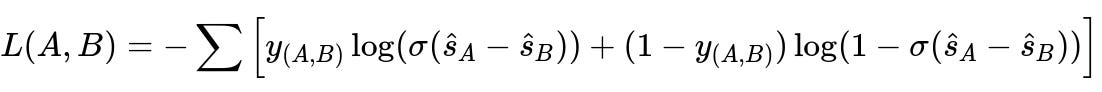ML Case-study Interview Question: Pinpointing Delivery Locations: Pairwise Ranking ML for Noisy GPS Data
Case-Study question
Imagine you work for a large-scale delivery platform that often struggles to pinpoint the exact drop-off location for many addresses. Drivers sometimes park far from the doorstep due to uncertain GPS signals. The street-facing centroid of the location data can make them even more confused, leading to wasted time and possible delivery delays. You have access to historical GPS tracks from past deliveries, but this data is noisy and inaccurate. You also have limited map information like street layouts and building footprints. Propose how to use machine learning to solve this precise geolocation problem. Provide a full solution with modeling approaches, data feature engineering, candidate point generation, and final deployment strategy. Discuss how you would measure success and mitigate inaccuracy or incomplete map data. What key obstacles do you foresee, and how will you address them?
Please outline your strategy in a thorough, step-by-step manner, as if you are guiding a team of data scientists and software engineers to implement it.
In-depth solution
Overview of the approach
Use a supervised learning method that ranks potential doorstep locations. The goal is to choose the candidate point that best represents the true drop-off location. Past GPS data for each address is noisy because drivers can confirm deliveries while still on the street or near the vehicle. A ranking-based model can handle multiple candidate points and decide which candidate is most likely correct.
Key components of the solution
Maintain a dataset of repeated deliveries to the same addresses. Consolidate multiple noisy GPS observations and label the actual doorway location when known. Generate a set of candidate points for each address, drawing from historical GPS clusters and map-based features (building polygons, proximity to roads, and so on). Train a model to learn pairwise preferences: for any two candidates, the model learns which one is more likely the true doorway.
Central formula for pairwise learning-to-rank
Here is a core pairwise preference function, where you compare two points A and B for a given address:
Centered meaning of each symbol:
AandBare two candidate points for the same address.y_{(A,B)}is 1 ifAis closer to the true doorway thanB, else 0.\hat{s}_Aand\hat{s}_Bare the scores assigned by the model to each candidate.\sigmais the logistic function for mapping the difference( \hat{s}_A - \hat{s}_B )to a probability.This summation extends over all training comparisons within a batch. The model updates weights to favor the correct preference.
Feature engineering
Each candidate point has a feature vector: density features (number of past GPS pings around it), map-distance features (distance to the nearest street, distance to the nearest building corner), and contextual features (number of deliveries at this address, existence of building outlines). The model uses these features to score each candidate.
Model architecture and training
A random forest or gradient-boosted trees can work well. It ingests two candidate points at a time, produces a preference, and uses a pairwise loss function. After training, for inference, compare all candidates for a given address pairwise. Choose the point that wins the most pairwise contests as the final geolocation.
Candidate point generation
Filter raw GPS points: remove extreme outliers, merge dense clusters, and add any relevant building outline edges. This yields a small set of distinct candidate locations for each address. If map data is partial, rely more on GPS clustering. If building footprints exist, place some candidates along building perimeters.
Handling incomplete map data
Train the model to recognize when building footprints are missing or incomplete. Features like “distance_to_building” or “distance_to_road” can be set to some large or default value when missing. The model can still rely on the density-based features from repeated deliveries.
Deployment strategy
Precompute the best predicted doorway coordinates for each address with enough historical data. Store them in a lookup table or geospatial index. When a new delivery is made, the driver’s app shows the predicted location. If the location is still off, the corrected coordinates can be captured for retraining.
Evaluation metrics
Use distance-based errors: measure the distance between the model’s predicted location and the ground-truth doorway coordinates (in a labeled dataset). Track the median or 90th-percentile error. Compare to simpler baselines like centroid or kernel density. Improvements reduce driver confusion and shorten delivery times.
Practical considerations
Secure high-quality labeled door coordinates to bootstrap the model. Introduce a feedback mechanism for drivers to correct predicted doorways. Implement robust outlier detection so that sporadic or partial GPS data does not ruin the training set.
Example code snippet
import numpy as np
from sklearn.ensemble import RandomForestClassifier
# Suppose X_pair is an array of feature differences for each candidate pair
# y_pair is 1 if candidateA is better than candidateB, else 0
rf = RandomForestClassifier(n_estimators=30, max_depth=10)
rf.fit(X_pair, y_pair)
# Inference: compare each candidate point's pairwise votes
def rank_candidates(candidates):
wins = [0]*len(candidates)
for i in range(len(candidates)):
for j in range(i+1, len(candidates)):
# Feature difference between i and j
x_diff = extract_features(candidates[i], candidates[j])
prob_i_better = rf.predict_proba([x_diff])[0][1]
if prob_i_better > 0.5:
wins[i] += 1
else:
wins[j] += 1
best_index = np.argmax(wins)
return candidates[best_index]
This basic structure illustrates how to do pairwise comparisons offline.
Possible follow-up questions
1) How would you ensure the model generalizes to new or rarely visited addresses?
Train a unified model across many addresses so that latent patterns (for instance, building shapes or typical GPS noise distribution) transfer. For addresses that appear seldom, rely on general map features: distance from the street, building edges, or typical vehicle parking patterns. If little data is available, keep a fallback to a centroid-based approach until more deliveries accumulate.
Explain that as new deliveries happen, store the driver’s GPS tracks. Re-run the candidate generation process to refine the predicted location. Over time, the system transitions from a general guess to a more specialized location estimate.
2) Why is pairwise ranking preferred over a direct regression approach for location prediction?
A direct regression tries to guess actual latitude and longitude coordinates directly. This is risky because the training labels can be inconsistent (drivers confirm deliveries at random spots). Pairwise comparisons harness relative preferences, which are easier to learn from noisy data. Also, pairwise ranking can incorporate map-based constraints, giving robust results even with partial or scattered GPS pings.
3) How do you handle multi-modal distributions of GPS data?
Multi-modal distributions happen when the driver sometimes parks on one street and sometimes on a different street. A simple centroid might pick a point in the middle of the street. By generating multiple candidate clusters, the ranking model can decide which cluster is most likely correct. Building map outlines help ensure the final decision is near a legitimate doorstep, not the center of the road.
4) How can you reduce computational cost when you have many addresses?
Use the offline approach: for each address, do pairwise comparisons among 50 to 100 candidates. This is feasible in a batch job. Store the resulting best location. For addresses receiving frequent deliveries, refresh the model’s predictions on a scheduled cadence. This arrangement prevents excessive real-time computation.
5) What if the map data is unreliable or incomplete?
Explain that the system is designed to be map-agnostic. If building shapes are missing, the model can still rely on GPS clustering features. Model training must incorporate flags that indicate missing map data so that the algorithm does not expect building-distance features. Over time, improvements in map coverage produce better candidate generation.
6) How do you evaluate success beyond pure distance metrics?
Discuss real-time delivery efficiency, such as driver idle time, or how often the driver has to re-park to correct mistakes. Large improvements in these operational metrics confirm that the predicted locations are helpful in practice. You could also gather direct driver feedback in a user interface to confirm the predicted location’s correctness. Field experiments and A/B tests will measure if the system truly cuts delivery time.
7) How do you handle outliers in GPS data?
Tag outliers using robust distance thresholds. If a single GPS ping is hundreds of meters away from the others, filter it out. Alternatively, cluster the data, discard small clusters unless repeated in multiple visits, and let the main cluster dominate the candidate generation.
8) What if the learned ranker incorrectly selects a location in the street?
In training, add strong penalties or negative examples for street or parking-lot points (for instance, label them as suboptimal in the pairwise comparisons). Use mapping data to mark these as invalid doorways. Emphasize building-edge or walkway features. Provide a fallback check in the final selection phase: if the top candidate is in the street, pick the next best if it passes a distance threshold to the building.
9) How do you incorporate real-time driver feedback into the system?
Give the driver a quick interface to confirm or override a final predicted location. If the driver corrects it, log the exact location. Retrain weekly with the newly labeled data. This ensures the system converges on high-accuracy predictions.
10) How do you ensure fairness or coverage in more rural or under-mapped regions?
Include region-based data. If the address is in a low-density area, rely more on GPS cluster signals than on building outlines. Encourage expansions of map coverage, but design a fallback that does not require complete or updated map data. The robust pairwise ranking approach, anchored in historical GPS, can still find the best cluster location in these areas.
These comprehensive answers show the end-to-end reasoning for solving a noisy-GPS geolocation problem using a ranking-based machine learning system. The model architecture, feature engineering, data handling, evaluation, and real-world feedback loops form a complete solution.