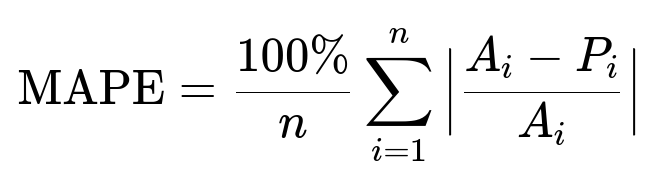ML Case-study Interview Question: Budget Optimization for GMV: Forecasting Saturation Points with Generalized Additive Models.

Browse all the ML Case-Studies here.

Case-Study question

A marketplace wants to optimize its marketing budget for maximum Gross Merchandise Value (GMV). Each day has budget spent and GMV observed. Historical data spans multiple cities. The goal is to forecast GMV at different budget allocations, find the tipping point where more budget yields diminishing returns, and ensure prediction error remains under acceptable thresholds. How would you approach this?

Detailed solution approach

Data Granularity

Gather daily data rather than weekly or monthly. Monthly or weekly aggregation loses fine-grained patterns, causing higher prediction error. Daily data preserves nuances, enabling better forecasts.

Error Metric

Use Mean Absolute Percentage Error (MAPE) to assess forecast accuracy.

A_i is the actual GMV on day i. P_i is the predicted GMV on day i. n is the number of predictions.

Choose MAPE if outliers significantly affect performance. A MAPE near 10 percent indicates relatively good accuracy for daily forecasts.

Baseline with Linear Regression

Start with a simple linear regression. It assumes GMV grows linearly with budget. Results showed it fails to capture saturation. Real-world budget returns plateau after a threshold, not forever increasing.

Polynomial Regression

Try polynomial regression to capture a nonlinear, logarithmic-like pattern. It detects a tipping point but slopes downward afterward, which is unrealistic. Budgets beyond a threshold should flatten GMV, not decrease it.

Tree-Based Models

Decision trees and random forests produce low error and a reasonable curve. They often generate stepped predictions: different budgets yield the same GMV forecast in certain ranges. This lack of granularity can be problematic.

Generalized Additive Model (GAM)

Adopt GAM to combine interpretability with flexibility. It handles nonlinear relationships and imposes smoothing so GMV never sharply declines after the tipping point. It provides reasonable error under 10 percent and a proper plateau shape. Regularization helps avoid overfitting. Interpretable partial dependence plots clarify how each feature influences GMV.

Sample Python Code

from pygam import LinearGAM, s
import numpy as np
import pandas as pd

# Assume df has columns: 'budget' and 'gmv'
X = df[['budget']].values
y = df['gmv'].values

# Define a smoothing spline for budget
gam = LinearGAM(s(0)).fit(X, y)

# Predict GMV at new budget levels
new_budgets = np.linspace(0, 10000, 100)  # example range
predicted_gmv = gam.predict(new_budgets.reshape(-1,1))

Explain or tune smoothing parameters using cross-validation to avoid over-smoothing or under-smoothing. Inspect partial dependence to confirm the plateau.

How would you handle seasonality or special events?

Incorporate extra variables like day-of-week or holiday indicators. GAM can include multiple smooth functions: one for budget, one for time-based seasonality. Each smooth term captures separate effects.

Why choose GAM over tree ensembles?

Tree ensembles often produce stepped predictions that lack fine differentiation at close budget values. GAM provides smoother transitions while preserving interpretability and controlling model complexity.

How do you ensure the model handles city differences?

Include city-level features or treat each city separately. Consider city as a categorical variable. Fit separate GAMs if usage patterns differ drastically, or build one GAM with city dummy variables.

How do you evaluate model performance beyond MAPE?

Check residual plots for bias. Inspect how errors distribute across different budget ranges. Compare performance on a holdout set. Track final business metrics, such as actual GMV lift after implementing model-based budget allocation.

Could overfitting arise with daily data?

Overfitting may occur if daily signals include too much noise. Regularize or add smoothing. Perform out-of-sample validation. Monitor MAPE on fresh data to ensure generalization.

---