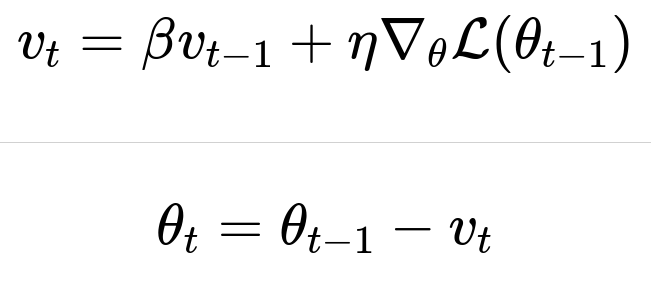ML Interview Q Series: Accelerating Gradient Descent with Momentum: Faster Convergence and Escaping Plateaus
📚 Browse the full ML Interview series here.
Momentum in Gradient Descent: What is momentum in the context of gradient-based optimization? *Write the update equations for gradient descent with momentum* and explain how momentum helps accelerate convergence and can help escape local minima or plateaus.
Momentum in gradient-based optimization refers to a technique inspired by the concept of physical momentum. Instead of using the gradient directly to update parameters at each step, momentum accumulates a velocity vector in the direction of persistent decrease of the loss function. This results in faster convergence, reduces oscillations, and helps the optimization process escape flat regions or shallow local minima.
How it works can be explained by imagining a ball rolling down the loss surface: instead of stopping at every step to re-calculate the gradient from scratch and move only in that direction, momentum integrates the velocity from previous steps, making it easier to keep going downhill in the same direction if that direction consistently reduces the loss.
Accelerating Convergence and Escaping Plateaus comes from the fact that when gradients keep pointing in a similar direction, the accumulated velocity (which is basically a running average of past gradients) helps us make larger steps. By contrast, in directions where the gradient might flip back and forth, these changes tend to cancel out in the velocity term, resulting in less wasted movement. On flat regions (or plateaus) where gradients are small, momentum can accumulate over many steps and “push” the parameters out of that plateau more quickly than vanilla gradient descent might.
Below are the main update equations (using the simplest classical momentum form). At each time step t, we have a velocity vector and parameter vector:
Here is an in-depth explanation of each term:
When β is close to 1.0, a large fraction of the old velocity is preserved between steps; when it is lower, the old velocity decays more quickly, and the update behaves more like standard gradient descent. The factor η is still your learning rate, controlling the scale of the gradient contribution.
Sub-Heading: Detailed Insights into Momentum’s Advantages
Momentum combines recent history of gradients so that if the loss has been decreasing in roughly the same direction for multiple steps, momentum “speeds up” the updates along that direction. This effect helps:
Address high-curvature ravines where naive gradient descent can oscillate widely from side to side, so momentum smooths the oscillations and leads to faster descent down the ravine.
Push through plateaus or saddle points where gradients are very small but consistent in one direction.
Potentially avoid some local minima (though in high-dimensional deep networks, local minima are not the only concern; plateaus and saddle points are often more problematic).
Sub-Heading: Practical Tips for Using Momentum
Typical values for β can range from 0.8 to 0.99, with 0.9 or 0.99 being common defaults. One must tune β alongside the learning rate η to ensure stable convergence. If β is too high, the updates might overshoot minima severely. If β is too low, momentum provides little benefit.
Sub-Heading: Example Implementation in Python
Below is a simple Python snippet illustrating how one might implement momentum-based gradient descent. In real-world practice, frameworks like PyTorch or TensorFlow handle these details, but this simple code helps conceptualize the update mechanism:
import numpy as np
# Suppose we have:
# - params: a NumPy array of parameters
# - grad: a NumPy array representing the gradient of the loss w.r.t. params
# - v: a NumPy array for the velocity (initialized to zeros)
# - eta: learning rate
# - beta: momentum factor
def momentum_update(params, grad, v, eta, beta):
# Update velocity
v = beta * v + eta * grad
# Update parameters
params = params - v
return params, v
# Example usage:
params = np.array([0.0, 0.0]) # Dummy initial parameters
v = np.zeros_like(params)
eta = 0.01
beta = 0.9
for iteration in range(100):
grad = compute_gradient(params) # compute_gradient is a placeholder
params, v = momentum_update(params, grad, v, eta, beta)
This simple function shows how each iteration, we scale the old velocity v by β and then add η⋅grad. We then update parameters by subtracting the new velocity. Notice how the velocity accumulates gradient information from multiple time steps.
Sub-Heading: Challenges and Further Developments
While momentum helps reduce some problems with standard gradient descent, it does not adapt the learning rate to different features of the parameters. Methods such as Adam or RMSProp incorporate concepts of adaptive learning rates along with momentum-like mechanisms. But classical momentum remains a robust and simple technique frequently used in practice.
Sub-Heading: Potential Interview Follow-Up Questions and Answers
What if the learning rate is set too high when using momentum?
A high learning rate combined with a high momentum factor can cause updates to overshoot the optimum. Because momentum accumulates velocity, if the step size is also large, the combined effect can make the parameter updates unstable. It is often best to reduce the learning rate slightly when adding momentum, or at least to tune it carefully to avoid divergence.
Does momentum always speed up convergence in every dimension of parameter space?
Momentum tends to reduce oscillations in directions where the gradient alternates significantly, but it also accumulates velocity in directions where gradients consistently point the same way. So while momentum can accelerate learning in directions that lead downhill, in directions with conflicting signals, the velocity may not necessarily be beneficial. This can lead to subtle effects in highly non-convex landscapes. Overall, it typically helps, but it’s not guaranteed to do so uniformly in every parameter dimension.
How does momentum help escape local minima or plateaus?
In many regions of the loss surface, particularly plateaus or shallow local minima, the gradient alone might be very small, leading to microscopic parameter updates that can keep the optimization from making progress. With momentum, the velocity term might accumulate over multiple steps, creating a stronger “push” once there is even a small, consistent gradient in a particular direction. This increased push can get you out of plateaus or shallow local minima more effectively.
Could momentum cause the optimizer to skip over a good minimum?
Yes, if the velocity is large and the learning rate is not well-tuned, the update steps might overshoot a narrow minimum. However, typical hyperparameter tuning with momentum (slightly reducing the learning rate, or decreasing momentum coefficient if overshooting occurs) usually mitigates this issue. When combined with well-chosen schedules that reduce learning rate over time, the risk of missing “good” minima is reduced.
How does one initialize the velocity term?
A standard practice is to start with v=0 for all parameters. As training begins, v is updated over the first few steps. Some frameworks initialize the velocity buffer to zero at the start and maintain a separate velocity buffer for each parameter. Using zeros is the simplest choice and is typically sufficient since velocity builds up quickly during training.
Does momentum help for every type of neural network architecture?
Momentum generally helps in training a wide variety of architectures, from simple feedforward networks to convolutional neural networks and recurrent networks, because the underlying principle—smoothing out noisy gradients and accumulating velocity in useful directions—remains beneficial across these cases. However, different architectures and tasks may require different hyperparameter choices for optimal performance.
How does momentum differ from Nesterov accelerated gradient (NAG)?
NAG is a variant of momentum that uses a “look-ahead” gradient. Instead of computing the gradient at the current parameters, you compute the gradient at the predicted next parameters. This often results in better theoretical guarantees and sometimes improves practical performance by taking into account where the parameters are likely to be after the momentum update. The classical momentum update does not do this look-ahead step.
Why is momentum often combined with learning rate scheduling?
Even with momentum, it is often beneficial to reduce the learning rate over time. As the optimizer gets closer to a minimum, smaller step sizes help avoid overshooting. Learning rate scheduling—such as exponential decay, step decay, or warm restarts—can be combined with momentum to gradually slow down updates while still enjoying the benefits of accumulated velocity. This synergy typically leads to more stable convergence late in training.
Could adding momentum harm performance if the dataset is extremely noisy?
In the presence of high variance gradients (e.g., from a very noisy dataset), momentum can accumulate velocity in a direction that might be dominated by noisy gradient signals. This can lead to suboptimal updates, at least temporarily. However, in practice, momentum often still improves convergence speed. If noise is severe, one might consider advanced optimizers (e.g., Adam) or tune momentum carefully (lower β) to avoid getting stuck from aggressive velocity accumulation.
Below are additional follow-up questions
How do you tune the momentum hyperparameter in practice?
One typical strategy starts with choosing a baseline learning rate and a standard momentum value (often 0.9 or 0.99). Then, one performs a small grid search or systematic experiment around these values. Because a larger momentum (β closer to 1) can amplify any overshoot, a good practice is to reduce the learning rate if you increase momentum. Here is a general outline:
Begin with a moderate β (e.g., 0.9) and a learning rate η previously found effective without momentum.
If training progresses stably, but convergence is slow, try increasing β (e.g., 0.95 or 0.99).
If training becomes unstable after you increase β, consider lowering η.
Monitor both training loss and validation metrics to ensure you are not overfitting or diverging.
Pitfalls:
If you set β too close to 1.0 without adequately adjusting η, the large accumulated velocity can cause the parameters to oscillate or diverge.
Very low momentum values (e.g., 0.5) might provide little advantage over plain gradient descent.
Different layers or parameter groups might benefit from different momentum values, so advanced frameworks sometimes allow per-parameter momentum settings if needed.
Edge cases:
In extremely noisy environments (e.g., very small batch sizes), high momentum can lead to high variance in updates and overshooting. Lower momentum is sometimes preferred in such settings.
In problems with severe non-convexity, momentum might get stuck in more complicated ways than standard gradient descent, so careful tuning is essential.
Could momentum reduce interpretability or transparency in monitoring training progress?
When using plain gradient descent, observing the loss curve gives a direct indication of how the immediate gradient influences parameters. However, with momentum, the update at each step is a combination of current and past gradients. This can slightly obfuscate the direct relationship between a gradient step and the parameter update. In practice, it might be less transparent to see exactly how the parameters move with respect to the instantaneous gradient.
Pitfalls:
A sudden jump in the loss may not correspond solely to the immediate gradient of the current mini-batch, but also to accumulated velocity from previous steps. This can cause confusion when debugging training.
Logging or checkpointing might capture parameter states that are influenced by a backlog of gradient signals.
Edge cases:
In tasks where interpretability of each gradient step is crucial (e.g., certain scientific computing tasks or critical decision-making systems), momentum can make it harder to pinpoint which step triggered a large update in parameter space.
Some domains with strict interpretability requirements might prefer simpler update schemes (even though they converge slower).
Does momentum address the problem of vanishing and exploding gradients in deep neural networks?
Momentum alone is not primarily designed to address vanishing or exploding gradients. It can mitigate exploding gradients by smoothing out some erratic updates (especially if the sign of the gradient flips rapidly from step to step), but it is not a panacea. If gradients are vanishing, momentum might eventually accumulate small signals and push parameters out of a dead zone, but the effect can be marginal if the gradients are extremely tiny.
Pitfalls:
Even with momentum, if the underlying network architecture (e.g., very deep RNNs) is prone to exploding gradients, you might still see numerical instability.
Vanishing gradients caused by improper activations (like saturating functions) or architecture design are not significantly resolved by momentum alone. Solutions usually require careful initialization or specialized architectures (like LSTM, skip connections, or batch normalization).
Edge cases:
In extremely deep networks, momentum might help marginally by adding small gradients across many steps, but this is often overshadowed by more direct methods like gradient clipping or advanced optimizers (e.g., Adam, RMSProp).
Is momentum beneficial in a distributed or asynchronous training environment?
In a distributed or asynchronous setting, multiple workers compute gradients in parallel. The accumulated velocity can still help smooth updates, but communication delays or staleness in gradient updates can complicate momentum’s effect. If a worker is using out-of-date parameters to compute gradients, the velocity term might accumulate in directions that are no longer valid in the updated global model state.
Pitfalls:
With asynchronous updates, the velocity might be based on old gradient information, causing momentum to accumulate in a direction that is no longer relevant.
Tuning momentum in distributed settings can be trickier, since the effective learning rate can vary as partial updates arrive from different workers at different times.
Edge cases:
Techniques like synchronous all-reduce training can preserve most benefits of momentum, but add overhead for synchronization.
In purely asynchronous methods (e.g., parameter server architectures), momentum can still be used, but it might require specialized adjustments or learning rate decay to remain stable.
What if we use a momentum factor greater than 1 or even a negative value?
Typically, β is chosen in the range [0, 1). If β>1, the old velocity is amplified rather than decayed. This can lead to extremely large updates and usually diverges in practice unless the learning rate is correspondingly tiny. Negative momentum values (less than 0) would flip the sign of the previous velocities, which generally does not make sense in typical gradient-based methods and can cause erratic parameter updates.
Pitfalls:
Even a value like 1.01 can cause runaway updates unless the learning rate is drastically lowered, and even then, it’s usually not stable.
Negative momentum or momentum factors well above 1 are rarely beneficial in typical machine learning tasks.
Edge cases:
There are some specialized research contexts exploring advanced momentum scheduling or alternative formulations, but these remain niche and are not standard in typical deep learning pipelines.
What is the difference between momentum and second-order methods like Newton’s method?
Momentum is a first-order method; it relies only on the first derivative (gradient). Second-order methods, such as Newton’s method or quasi-Newton methods (e.g., BFGS), incorporate the Hessian or its approximation to model curvature information. This generally allows for more direct “curvature-aware” steps, potentially leading to faster convergence for convex problems.
Pitfalls of second-order methods:
For high-dimensional neural networks, computing or approximating the Hessian is often infeasible due to memory or computational constraints.
Even approximate second-order methods can be very expensive for large-scale problems.
Why momentum is simpler:
Momentum adds negligible computational overhead compared to second-order approaches; you just maintain the velocity vector and do simple arithmetic.
Momentum is easy to integrate with mini-batch updates, while second-order methods typically need large-batch computations or approximations that can be complex to implement.
Edge cases:
In smaller scale or specialized problems, second-order methods might converge much faster than momentum-based SGD. But in deep learning with massive parameter spaces, momentum-based methods remain more practical.
In large scale production environments, what special considerations are there for momentum-based optimizers?
When training massive models on large clusters, one must consider efficiency and scalability of the momentum updates:
Memory overhead: Each parameter needs a separate velocity buffer. With billions of parameters, memory usage grows substantially.
Communication overhead: In distributed training, velocity updates need to be communicated alongside parameter updates, increasing network traffic.
Fault tolerance: If a worker crashes and loses the momentum buffer, the training process might become temporarily inconsistent. Frameworks often implement checkpointing that also saves the momentum terms.
Pitfalls:
If momentum buffers become unsynchronized across workers (in asynchronous mode), training might stall or produce suboptimal convergence.
Additional load balancing might be needed if certain workers handle bigger gradient computations.
Edge cases:
Some extremely large-scale training setups use more specialized optimizers (e.g., LAMB, Adafactor) tuned for distributed training. However, classical momentum is still used in many production systems because of its simplicity and reliability.
How does classical momentum compare to the heavy-ball method from classical optimization theory?
The heavy-ball method is essentially the formal name for the momentum approach introduced in classical optimization by Polyak. The update rule for the heavy-ball method is very similar to the standard momentum rule used in machine learning:
A “momentum” term β is multiplied by the previous update (the velocity).
The gradient term is then added to generate the new update.
In deep learning, “momentum” is effectively the same idea, though sometimes with minor variations in notation or interpretation.
Pitfalls:
In the context of classical convex optimization, the heavy-ball method has certain theoretical convergence rate guarantees. These do not directly translate to non-convex neural network loss surfaces.
Implementation details (like learning rate scheduling, mini-batching) were not central in the classical heavy-ball analyses and can alter the theoretical results.
Edge cases:
If a deep learning problem is nearly convex in some regions, the heavy-ball method’s known theoretical guarantees might partially apply, but in highly non-convex settings, the behavior is more empirical.
Does momentum treat large parameter subsets differently than smaller ones?
Momentum accumulates velocity component-wise; each parameter has its own velocity term. Therefore, if certain parameters consistently receive large gradients (perhaps because that part of the model is more sensitive or has a higher learning signal), the corresponding velocity accumulates more strongly. Conversely, parameters that see small or noisy gradients accumulate less velocity.
Pitfalls:
If some parameters consistently have larger gradients due to an imbalance in the network architecture or data distribution, momentum can create very large updates in those dimensions. This may destabilize training if the learning rate is not tuned or if gradient clipping is not used.
If certain parameters remain near-zero gradient for extended periods (either because they are saturating or because they are rarely updated), momentum may never accumulate enough velocity to move them significantly.
Edge cases:
In wide architectures where certain subsets of parameters are rarely activated by the data, those weights might remain nearly constant despite momentum.
In carefully regularized networks, large updates on certain parameters can be tempered by weight decay, partially offsetting the effect of strong momentum accumulation.
How does momentum interact with gradient clipping?
Gradient clipping limits the magnitude (or norm) of the gradient before it is applied to the parameter update. This is commonly used in recurrent neural networks or other architectures prone to exploding gradients.
If gradient clipping is applied before the momentum calculation, then even if the unclipped gradient is huge, the velocity update is capped, preventing unbounded growth in the velocity term.
If gradient clipping is applied after summing the momentum update, this can also help but might behave less predictably.
Pitfalls:
Inconsistency in where clipping is applied can cause confusion. Some frameworks clip gradients before adding them to the momentum buffer, others after.
If you do not clip the momentum term itself, it might grow even after the gradient portion is clipped. One approach is to clip the entire parameter update, including the momentum accumulation.
Edge cases:
For tasks with extremely large or sudden gradient spikes (e.g., in certain reinforcement learning scenarios), you may need to clip very aggressively or in specialized ways (e.g., block-wise clipping).
With mild gradient spikes, momentum itself might partially mitigate the effect by combining the spike with prior velocity, but in extreme cases, you still need explicit clipping.
Can momentum lead to overfitting more quickly than vanilla gradient descent?
Momentum can speed up descent, allowing the model parameters to converge to a low training loss region faster. If the network has enough capacity to overfit the training data, faster convergence can also mean that the model might start overfitting sooner in wall-clock time or iteration count. However, overfitting eventually depends on whether the model is too flexible and whether regularization techniques are applied. Momentum itself does not inherently cause more overfitting in the final solution; it primarily changes the trajectory and speed of optimization.
Pitfalls:
Rapid progress on training loss may cause some practitioners to end training too late (if relying on heuristics that watch training loss rather than validation metrics).
If you tie early stopping strictly to the number of epochs (and not validation performance), momentum might cause you to overshoot the optimal epoch of training.
Edge cases:
In small or synthetic datasets, momentum might converge to a near-zero training loss extremely quickly, leaving little time to track generalization or apply early stopping.
If combined with high momentum and no regularization, the model might quickly memorize training examples, especially in small data regimes.
Are there any specialized momentum schedules or variants for non-stationary tasks?
Non-stationary tasks, such as certain reinforcement learning problems or time series prediction where the data distribution changes over time, might benefit from specialized momentum schedules that allow the optimizer to “forget” older gradients more rapidly. Some possible strategies:
Decreasing momentum over time: Start with high momentum to get fast initial convergence, then reduce it so that older gradients have less impact.
Periodic or cyclical momentum schedules: Oscillate momentum between two values, similar to cyclical learning rate strategies.
Adaptive momentum decay: Let the momentum factor dynamically adjust based on some measure of gradient drift or performance metrics.
Pitfalls:
If the task’s distribution changes quickly, a high β can slow down adaptation because the velocity term keeps pushing in a direction that was relevant to older data distributions.
Poorly chosen schedules might degrade performance more than using a simple static momentum.
Edge cases:
Non-stationary environments that drastically shift (e.g., domain shifts or concept drifts) may require more advanced techniques like meta-learning or adaptive optimizers that incorporate momentum-like terms while also reacting quickly to new data patterns.
In partially observable or delayed reward settings, momentum might accumulate spurious gradients if the model repeatedly sees misleading signals. A well-designed schedule or an algorithm with an adaptive reset of velocity can help.