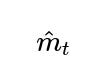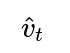ML Interview Q Series: Adam Optimizer: Adapting Learning Rates with Gradient Moment Estimates.

📚 Browse the full ML Interview series here.

Adam Optimizer: Adam is a popular optimizer in deep learning. Explain how Adam adapts the learning rate for each parameter (hint: it uses estimates of first and second moments of gradients). Why might Adam converge faster or more reliably than standard SGD in practice?

How Adam Adapts the Learning Rate for Each Parameter Adam uses adaptive estimates of lower-order moments of gradients. Specifically, it computes an exponential moving average of both the first moment (the mean of the gradients) and the second moment (the uncentered variance of the gradients). In practice, these moving averages are referred to as the “moment estimates.” The optimizer then uses these moment estimates to adapt the effective learning rate for each parameter dimension.

The idea of adaptive learning rates is that parameters with consistently large gradients should be scaled down (to avoid overshooting), while parameters with consistently small gradients should be scaled up (to move them more quickly in the right direction). This is done via division by the root of the second moment estimate (plus a small epsilon for numerical stability), which prevents overly large updates and helps stable training.

Fundamental Mechanics of Adam’s Updates Adam maintains two primary variables for each parameter:

The first moment estimate (often denoted by m): This is the exponential moving average of the gradients.

The second moment estimate (often denoted by v): This is the exponential moving average of the elementwise square of the gradients.

In code or pseudo-mathematical format, each parameter’s update rule can be summarized (conceptually) as follows:

Here,

is the bias-corrected first moment estimate, and

is the bias-corrected second moment estimate. These bias corrections are especially important at the beginning of training, when the exponential moving averages are initially close to zero. The hyperparameter

ϵ

is a small constant (like 1e-8) added to avoid division by zero.

Why Adam Can Converge Faster or More Reliably than Standard SGD Standard Stochastic Gradient Descent uses the same global learning rate for all parameters. When gradients vary significantly in scale across different dimensions, SGD can be slow to converge in directions with tiny gradients and can oscillate or overshoot in directions with larger gradients.

By contrast, Adam’s division by the square root of the second moment estimate effectively normalizes parameter updates. That can lead to:

Better stability and less sensitivity to hyperparameter tuning. Consistent step sizes for each parameter dimension, which helps avoid the problem of one dimension overshadowing others. Faster convergence in practice because it can pick up small but consistent signals in gradients more quickly. Reduced need to meticulously tune learning rates throughout training.

Implementation Details in Practice Using Adam in a modern deep learning framework (PyTorch or TensorFlow) typically looks like this:

import torch
import torch.nn as nn
import torch.optim as optim

model = nn.Linear(10, 1)  # Just a simple example model
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)

# Training loop
for epoch in range(num_epochs):
    for x_batch, y_batch in data_loader:
        optimizer.zero_grad()
        predictions = model(x_batch)
        loss = criterion(predictions, y_batch)
        loss.backward()
        optimizer.step()

In this snippet, Adam automatically updates the first and second moment estimates behind the scenes for each parameter in the model. This shows how easy it is to switch from standard SGD to Adam by changing the optimizer choice and possibly adjusting the learning rate hyperparameter.

Potential Pitfalls when Using Adam Choosing hyperparameters: Even though Adam is somewhat less sensitive to the learning rate, picking an extremely large or small learning rate can still cause convergence issues. Early biases in the moving averages: The exponential moving averages are bias-corrected, but if the training batch size is very small or if the data is not representative, the early gradient estimates can be somewhat noisy. Tendency to converge to sharp minima in some cases: Some research suggests Adam can converge to local minima that may be less generalizable, although in practice, it usually still works well.

Scenarios Where Adam Particularly Helps Models with sparse gradients: When the gradient for certain parameters is sparse or rarely nonzero (like embeddings in NLP tasks), Adam’s adaptive nature can give bigger learning rate boosts to those rarely-updated parameters. Complex architectures: In large-scale models with thousands or millions of parameters, certain layers might have drastically different gradient magnitudes. Adam can handle these scaling issues more gracefully than plain SGD. Moving target scenarios: In reinforcement learning or scenarios with non-stationary data distributions, Adam can more rapidly adjust learning rates over time.

Practical Tips Try default betas (e.g., 0.9 for the first-moment decay, 0.999 for the second-moment decay) when starting out. These are commonly used and tend to perform well in many tasks. Monitor training curves to check whether the learning rate is too large or too small. For very large models, warmup schedules or decaying the learning rate can sometimes help even further. Keep an eye on the effective step sizes. If they get too small or vanish, you may need to reduce weight decay, reduce the second-moment decay (beta2), or slightly increase the learning rate.

How Do the Bias Corrections Work in Adam?

Adam includes bias correction terms because the exponential moving averages (for both the first and second moments) start off at zero and then gradually incorporate gradient information. Without bias correction, the early steps of training might use moment estimates that are systematically biased low. The corrected estimates effectively divide by a factor related to

(for the first moment) and

(for the second moment). This way, the optimizer can make more accurate adjustments early in training.

Why Do We Add Epsilon to the Denominator in the Adam Update Rule?

The epsilon term is crucial for numerical stability. If the second moment estimate

is extremely small (or zero), dividing by zero or an extremely small number can result in updates that blow up. By adding a small constant like 1e-8, the magnitude of the updates is kept in a safe range. This also ensures that the direction of the update vector is preserved without introducing wild fluctuations.

Are There Cases Where Plain SGD Might Outperform Adam?

Yes. On certain well-conditioned problems or tasks with simpler data distributions, plain SGD (especially with momentum) can match or outperform Adam. SGD can sometimes help the model find solutions that generalize better, especially if the default Adam hyperparameters aren’t tuned. In problems with certain types of regularity or smooth convex losses, the adaptive scaling in Adam might be less beneficial than a well-tuned SGD with momentum. However, for most large, complex modern models, Adam tends to work well or at least be a strong baseline.

How Does Adam Compare to Adaptive Methods like RMSProp or Adagrad?

Adam generalizes some of the concepts from these earlier optimizers:

RMSProp: Maintains an exponential moving average of squared gradients but does not keep a separate first-moment moving average. Adagrad: Accumulates the sum of squared gradients over time and adjusts learning rates, but it can become very small for some parameters as training progresses. Adam uses the best of both worlds by keeping a running average of the gradients themselves (like momentum) and a running average of the squared gradients (like RMSProp). This combination allows Adam to have momentum-like behavior while also adapting step sizes for each parameter dimension.

Is There a Recommended Default Configuration for Adam?

A common default is: Learning rate = 0.001 Beta1 = 0.9 Beta2 = 0.999 Epsilon = 1e-8

This configuration often performs quite well in many deep learning scenarios. However, for large-scale language models, sometimes the learning rate might be set to 0.0001 or changed adaptively during training with schedules like warmup and decay. Always consider using monitoring or validation performance to tune these hyperparameters.

Could Vanishing or Exploding Gradients Occur with Adam?

While Adam helps mitigate exploding and vanishing gradients by adapting learning rates, it does not entirely eliminate them. If gradients become very large for some reason (e.g., due to the architecture or data), Adam’s step size can still grow too large if the second moment estimate has not caught up yet. Conversely, with extremely small gradients, Adam might reduce the step sizes over time, leading to slow learning if certain parameters need to make large adjustments. In practice, you still want to ensure your network architecture is stable and data is normalized properly.

How Can One Debug or Visualize Adam’s Internal Statistics?

In some frameworks, you can access the internal state of the optimizer. For instance, in PyTorch:

for name, param in model.named_parameters():
    if param.grad is not None:
        state = optimizer.state[param]
        # This state typically has 'exp_avg' for m, 'exp_avg_sq' for v, etc.
        # You can check their norms or values

Monitoring these values can help you see whether certain parameters have extremely large or small moment estimates. This can guide you in deciding whether different betas or a different global learning rate is warranted.

How Do We Choose Between Adam and Other Optimizers in Practice?

When in doubt, Adam is often a strong and safe first choice. If you notice that your model is not converging or is diverging (loss explodes), you might try: Tuning the learning rate or betas. Switching to SGD with momentum if your problem domain is known to work well with it (e.g., certain vision tasks). Trying other optimizers like AdamW that implement decoupled weight decay.

In many production and research settings, Adam or AdamW remains the go-to option, especially for NLP or large-scale deep learning tasks.

Could Adam Get Stuck in Local Minima?

Any gradient-based method can get stuck in poor local minima or saddle points. Adam’s adaptive steps can help it jump out of shallow valleys or areas where the gradient is small, but there is no guarantee it will find the global optimum. Proper initialization, careful learning rate scheduling, and good regularization can help mitigate these issues.

Why Does Adam Sometimes Require Less Hyperparameter Tuning Than SGD?

Because Adam automatically adjusts step sizes based on gradient statistics, it tends to be more robust to suboptimal initial learning rates compared to raw SGD. With plain SGD, a learning rate that is too high or too low can drastically affect convergence. Adam’s second-moment normalization helps moderate these extremes, making it easier to find a stable training regime.

Is Adam Always Better for Non-Convex Problems?

It is not guaranteed to be strictly better in all non-convex problems, but it often is a strong performer in many large-scale or complex settings (like transformer-based language models). Non-convex optimization can be sensitive to factors like initial conditions, data variability, and architecture choices. Adam’s adaptive learning rate can help in navigating these conditions more gracefully. However, some specialized tasks or well-tuned momentum-based SGD can yield similar or better results.

Could Adam Overfit More than SGD?

Overfitting is primarily influenced by the model capacity and regularization rather than the choice of optimizer alone. However, because Adam can converge more quickly, it might reach a low training loss earlier. If there is insufficient regularization (dropout, weight decay, etc.), the faster convergence might lead to overfitting more quickly. AdamW, which decouples weight decay from gradient-based updates, is often used in practice to mitigate overfitting in large-scale models.

Does Adam Require Larger or Smaller Batch Sizes?

Adam does not strictly require a specific batch size. It can work with both small and large batch sizes. However, with extremely small batch sizes, the variance in the gradient estimates can be high, and so the moment estimates might be noisy. With large batch sizes, training can be more stable, but each update step might be computationally more expensive. In practice, Adam is often used with mini-batch sizes ranging from 32 to thousands, depending on the hardware and application.

How Might You Adjust Adam Hyperparameters When Training Giant Models like GPT?

In large-scale training scenarios, one might do the following: Use learning rate warmup during the initial training phase to avoid large, unstable updates. Use learning rate decay schedules (like cosine decay) after the warmup. Consider lowering the beta2 slightly (like 0.98 or 0.995) if momentum accumulation is too high. Use AdamW instead of vanilla Adam for better weight decay behavior.

All these adjustments help maintain stable training dynamics over long training runs.

Why is Adam So Popular in NLP tasks?

NLP tasks, especially those involving embeddings, often have sparse gradient updates in high-dimensional embedding matrices. Adam’s adaptive scaling can effectively handle these sparse updates by increasing the step size for those rarely updated parameters and controlling the step size for frequently updated parameters. It also reduces the burden of tuning learning rates extensively, which is crucial for the rapidly evolving, large-scale transformer architectures common in NLP.

Are There Performance Concerns with Adam?

Because Adam needs to maintain and update two sets of moment estimates per parameter (first moment m and second moment v), it has a slightly higher memory footprint than plain SGD. The additional memory overhead is about twice the size of the model parameters, which can be a concern for extremely large models. The computational cost is also incrementally higher, but typically not prohibitive. Most of the time, the benefits outweigh these downsides.

What is the Most Common Reason for Switching Away from Adam?

The most common reason is if you suspect that Adam is converging to a solution that is too shallow or not well-generalized, or if you can achieve better generalization and simpler hyperparameter tuning with SGD on a specific problem domain. Vision tasks on ImageNet, for instance, can often be effectively handled with SGD + momentum or variants like Nesterov momentum. Nonetheless, many practitioners still stick to Adam for convenience and robust performance across tasks.

---

Below are additional follow-up questions

How Does Adam Handle Outliers in the Gradient Distribution?

Adam calculates exponential moving averages for the first and second moments of gradients. Outliers can momentarily affect these moments, but due to the exponential decay, their influence gets damped if they do not consistently appear. Specifically, the second moment estimate (the exponential moving average of squared gradients) will temporarily rise if there’s a significant spike in gradient magnitude. This rise in the second moment causes the next updates to shrink. Hence, even if a single batch produces an abnormally large gradient, Adam reacts by increasing the denominator (the square root of the second moment estimate), thus reducing the effective step size.

However, in scenarios where outliers occur repeatedly, they can systematically distort the second moment. Adam will keep the step size small for those parameters until the outliers subside. If the data distribution frequently produces large, sporadic gradients (e.g., with very noisy data), it can lead to slower convergence. To mitigate persistent outliers:

• Gradient clipping is often used to keep the gradients within a sensible range.

• Data preprocessing or noise filtering techniques can help if the outliers are genuinely spurious.

A subtle pitfall arises when the dataset contains many repeated outliers in only a subset of parameter dimensions. In that case, those dimensions might continually see a high second moment estimate, and their effective learning rates could remain low, slowing down progress in that subset of parameters.

When Do the Betas Hyperparameters Matter the Most?

Adam uses two beta values:

• Beta1 controls how fast the first moment (mean gradient) decays.

• Beta2 controls how fast the second moment (variance) decays.

They matter most in the initial training phase or when gradients shift distribution quickly (as in non-stationary problems or when training large language models on highly varied data). For instance:

• A high Beta1 (e.g., 0.9) places a strong emphasis on historical gradients. If the distribution of gradients changes rapidly, this heavy emphasis can lag behind more recent information.

• A high Beta2 (e.g., 0.999) smooths the second moment significantly. If the data is noisy but mostly stable, this might be ideal. However, if your problem has abrupt changes in gradient magnitudes (e.g., from one phase of training to another), the second moment might adapt too slowly.

For real datasets like image data (ImageNet) or text corpora (GPT-like training):

• Beta1 = 0.9, Beta2 = 0.999 often work well initially.

• If you see that your updates are too large when data shifts, lowering Beta1 slightly (e.g., 0.85) can help adapt more quickly.

• If updates are getting stuck or are too small, you might reduce Beta2 so that the second moment can catch changes in variance faster.

Pitfalls include:

• Making Beta1 or Beta2 too large can lead to “momentum memory” that ignores new gradient information.

• Making them too small can lead to noisy updates because the moving averages won’t smooth out the gradient enough.

Is Adam Guaranteed to Do Better Than RMSProp in Any Scenario?

Adam is not guaranteed to outperform RMSProp universally. Both RMSProp and Adam share the adaptive learning rate concept through second moment tracking. The additional feature in Adam is the first moment (momentum-like) term. In some tasks, RMSProp can match or even exceed Adam’s performance if momentum is not crucial or if the specific combination of hyperparameters suits RMSProp better.

For example, in some reinforcement learning scenarios, researchers have historically favored RMSProp (partly for historical reasons and partly because of simpler hyperparameter tuning for certain tasks). In small or moderate networks, RMSProp with well-chosen hyperparameters might converge just as fast as Adam.

A subtle edge case is if the momentum term in Adam causes your model to overshoot local minima in a task where stable, slow descent is more beneficial. RMSProp does not have that momentum term by default, so it may yield more stable, albeit slower, convergence.

How Do You Debug Training Instability with Adam in Practice?

Training instability might manifest as:

• Sudden spikes or divergence in loss.

• Very noisy gradients.

• Extremely small or extremely large step sizes.

Debugging steps:

1. Monitor the learning rate: Check if the effective step sizes for certain parameters are exploding or vanishing. In PyTorch, for instance, you can look at the optimizer state dictionaries to see the “exp_avg” (first moment) and “exp_avg_sq” (second moment).

2. Check the data: Input data irregularities, such as huge outliers or corrupted samples, might cause extreme gradients. Visual inspection or statistical checks can identify these anomalies.

3. Use gradient clipping: Clip gradients to a fixed norm (like 1.0 or 5.0) to prevent out-of-control updates.

4. Experiment with smaller learning rates: Even though Adam is adaptive, a too-large global learning rate can cause rapid oscillations or divergence.

5. Adjust Beta1 or Beta2: If the second moment is updating too slowly, you might slightly lower Beta2. If momentum is too strong, you might slightly lower Beta1.

In real-world scenarios (e.g., large-scale NLP or computer vision):

• Implement advanced monitoring (like TensorBoard histograms or custom logging) to track gradients and parameter histograms.

• Carefully watch for large, abrupt changes in the distribution of any batch or layer outputs.

What Might Cause Adam’s Effective Learning Rate to Become Extremely Small, and How Do You Fix It?

The effective learning rate for a parameter is proportional to:

If

(the bias-corrected second moment estimate) grows large and remains large, the denominator will dominate, making the effective step size very small. Some reasons:

• Consistently large gradients: If your parameter sees high gradients for a sustained period, the second moment estimate grows, shrinking the step size.

• Very high Beta2: A large Beta2 means old squared gradients remain in the exponential average for a long time, so

  

  might stay large even if gradients decrease later.

• Inappropriate initialization: If the network or data processing leads to big gradients early, the second moment can balloon.

Fixes include:

• Lower Beta2: Let the optimizer adapt more quickly to changing gradient norms.

• Gradient clipping: Keep gradients within a maximum norm to prevent runaway second moment estimates.

• Layer normalization or careful architecture choices: This helps ensure stable gradient magnitudes.

• Learning rate scheduling: Sometimes a warm-up phase helps. A small initial learning rate can prevent early runaway second moments.

When Should We Combine Adam with Advanced Scheduling Methods Such as Cyclical Learning Rates or Warm Restarts?

1. Long training schedules: For large models (e.g., transformers or big CNNs) with many epochs, cyclical learning rates can help the model escape local minima or plateaus. The idea is to periodically raise and lower the learning rate, giving the model a chance to explore a variety of parameter configurations.

2. Non-stationary tasks: If the data distribution or task objectives change over time (like in some reinforcement learning or online learning scenarios), cyclical or warm restarts can help the model re-adapt.

3. Fine-tuning: When fine-tuning a pre-trained model, you might start with a small learning rate, then gradually increase it (warm-up), and eventually schedule it down again.

Warm restarts (sometimes referred to as SGDR, or Stochastic Gradient Descent with Warm Restarts) periodically reset the learning rate to a higher value, then let it decay. Adam can be combined with these methods similarly to SGD. The key is that Adam’s adaptive behavior and the cyclical/warm restart schedules can work in tandem to find deeper minima while still adjusting each parameter’s step size automatically.

Pitfalls:

• Overcomplicating the schedule may lead to confusion about which hyperparameter is controlling training dynamics at any given moment.

• If your dataset or model is small, advanced scheduling might be unnecessary overhead.

How Does Adam Interact with Batch Normalization? Any Issues or Best Practices?

Adam and batch normalization typically work together fine. Batch Normalization normalizes activations across the current mini-batch, helping keep forward passes stable. Meanwhile, Adam controls the parameter update magnitudes.

Potential issues:

• Small batch sizes: Batch Normalization can become noisy, and Adam might overfit to that noise if not tuned carefully. In these cases, you might want to use Group Normalization or Layer Normalization instead of Batch Normalization, or at least test different Beta1/Beta2 or add gradient clipping.

• Bias correction: BatchNorm layers have separate learnable parameters (scale and shift). Adam updates these too. In principle, there’s no issue, but watch if the batch statistics are extremely noisy, as it can cause large updates or instability for these parameters.

Typically, the default Adam parameters work well with BatchNorm, but you should:

• Ensure the batch size is sufficiently large for stable BN statistics.

• Monitor any unusual divergence or exploding updates in the BN parameters.

How Do We Interpret the Gradient Flow With Respect to Adam’s Internal States?

1. First moment (exp_avg): Tracks the direction and magnitude of gradients over time. If a parameter’s gradient is consistently positive, its exp_avg will be strongly positive, leading to negative updates (since we move in the opposite direction of the gradient).

2. Second moment (exp_avg_sq): Tracks the variability or “energy” of the gradient. If a parameter has large fluctuations, exp_avg_sq grows, shrinking the step size.

Interpreting them together:

• If exp_avg is large and exp_avg_sq is moderate, the parameter gets a decent update in the direction of the negative gradient.

• If exp_avg_sq gets very large, the denominator grows, shrinking updates even if exp_avg remains significant.

In practice, visualizing these can provide insights into which parameters are consistently receiving strong gradient signals (large exp_avg) and which parameters have unstable or spiking gradients (large exp_avg_sq). Large second moments may indicate layers or parameters that are heavily influenced by the data distribution’s variability (e.g., final classification layers in a model that sees diverse classes).

Could Adam Overemphasize Certain Gradient Directions Due to Persistent Correlation in the Data or Parameter Updates? How to Fix That?

Yes, if certain features or layers see consistent gradient correlations (e.g., in a skewed dataset where certain classes or tokens dominate), Adam’s first moment can accumulate in that direction. Even though the second moment is also increasing, the net effect can be that the update direction remains biased.

Possible fixes:

• Better data balancing: If your training data is skewed, the optimizer can reinforce that skew. Balancing or augmenting data may alleviate the bias in gradient directions.

• Adjust Beta1: A slightly lower Beta1 can reduce the “build-up” effect of correlated gradients.

• Use weight decay or regularization: This helps keep parameter magnitudes in check. AdamW specifically decouples weight decay from gradient-based updates, preventing parameter drift in certain directions.

• Look at layer-wise learning rates: If only one layer is suspect, you could apply a different or smaller learning rate to that layer. Some practitioners do partial freezing or per-layer LR to ensure that heavily correlated gradients do not dominate the entire update.

What Happens in the Presence of Gradient Clipping? Is It Recommended with Adam?

Gradient clipping ensures that the global norm (or the norm of each parameter group) of the gradient does not exceed a specified threshold. With Adam, clipping is often used to avoid exploding updates especially in recurrent neural networks or in transformer architectures where gradients can spike unpredictably.

• Mechanics: If the norm of the gradient exceeds the threshold, all gradient components are scaled down proportionally. Then Adam applies its usual adaptive scaling based on m and v.

• Benefits: Prevents catastrophic updates from extreme batches or ill-conditioned steps.

• Potential downside: If clipping is too aggressive, it might hamper the optimizer’s ability to make sufficiently large updates when needed.

• Recommendation: Many large-scale training protocols in NLP or computer vision do incorporate gradient clipping with Adam (commonly a clipping norm of 1.0 or 5.0).

The key point is that the clipped gradient is still processed by Adam’s first and second moment accumulators, so Adam’s adaptivity remains. However, the second moment might not fully capture the scale of the unclipped gradient if you frequently rely on clipping. This is usually acceptable since the point is to avoid out-of-control steps.

How Does Adam Handle Partial Freezing of Certain Layers in a Pretrained Model?

When freezing layers, you typically remove their parameters from the optimizer’s parameter list. In other words, those layers’ weights are no longer updated, so Adam does not maintain first or second moment estimates for them. The partially frozen layers remain fixed, while the remaining layers’ parameters continue to be updated with Adam as usual.

Considerations:

• If you plan to unfreeze those layers later (a common technique in progressive unfreezing or layered fine-tuning), you might reintroduce them to the optimizer with reset moment estimates. If you keep the old moment estimates from a previous stage, they might not reflect the new training context or updated data distribution.

• Frozen layers can still accumulate gradient if you haven’t explicitly told the framework to skip them during backprop, but if the gradient is never used to update the parameters, it’s effectively inert. Ensure your code is set so that these gradients are not even computed if you want to save memory and computation time.

How Does the Combination of Adam with Distributed Training or Mixed-Precision Training Affect Performance and Stability?

1. Distributed Training (Data Parallel):

   • Each worker computes gradients on its mini-batch. Then the gradients are aggregated (by averaging or summation). Adam’s moment estimates are updated after the aggregated gradient is formed. This can make the second moment computation more stable (because it’s based on more data per step).

   • Communication overhead grows if the model is large, especially since Adam requires maintaining m and v for each parameter. In frameworks like PyTorch Distributed Data Parallel, this overhead is usually well-optimized, but it is still higher than SGD’s overhead.

2. Mixed-Precision Training:

   • Gradients are stored in lower precision (e.g., float16), which can introduce numerical rounding. Adam’s second moment update is sensitive to these small errors.

   • Many frameworks use loss scaling to handle this, ensuring gradients are not underflowing to zero. The moment estimates might also be kept in higher precision (float32) to preserve stability.

   • If not done carefully, the second moment (exp_avg_sq) could be too small or too large due to precision constraints, affecting the updates. Ensuring correct loss scaling typically alleviates these issues.

In practice, combining Adam with distributed or mixed-precision training is standard for large-scale tasks, but it requires consistent validation that the updates remain numerically stable and that no subtle overflow/underflow issues are happening in the moment accumulations.

Could Adam Cause Slower Training for Very Simple or Shallow Models?

It can happen if the overhead of maintaining and updating first and second moment estimates outweighs the benefits of adaptive learning rates. For a small, shallow model with relatively easy gradients, vanilla SGD or SGD with momentum might train faster (especially if the batch size is large). Also, Adam’s overhead in memory can be unnecessary for a small model.

Additionally, if the problem is convex or near-convex and well-conditioned, the advantage of adaptive steps might be minimal. In these cases, well-tuned SGD with momentum could converge just as fast or faster and be simpler to implement or debug.

What Are Some Real-World Cases Where Adam Fails to Converge, and How Do We Address Those Failures?

1. Unstable architectures: Some network architectures can yield extremely large activations and gradients (e.g., recurrent networks without proper gating or normalization). Adam might reduce the effective learning rate but still not enough to prevent divergence.

2. Inadequate data preprocessing: If input features are unscaled or have extreme ranges, gradients might be erratic. Even an adaptive optimizer may struggle.

3. Poor parameter initialization: If weights are initialized so that some layers produce extremely large outputs, Adam’s early steps might blow up.

4. Excessively high learning rate: Despite adaptivity, if the base learning rate is extremely large, the second moment might not scale quickly enough to rein in updates before divergence.

Addressing these issues:

• Proper data normalization or standardization.

• Carefully chosen initialization (e.g., Xavier or Kaiming init).

• Using smaller initial learning rates and possibly a warm-up schedule.

• Checking for architecture design flaws, such as missing normalization layers or incorrectly placed skip connections.

How Does Adam’s Performance Vary Across Different Activation Functions or Network Topologies?

1. Activation functions:

   • ReLU or variants: Tends to produce sparse gradients for negative inputs. Adam can adapt well to those layers that receive very few non-zero gradients, giving them slightly larger updates relative to their gradient signal.

   • Sigmoid or tanh: These saturate for large positive or negative inputs. Adam can still help by adapting the step sizes, but if the entire network saturates, no optimizer can help much. Proper initialization and architecture design are more crucial.

   • Swish, GELU, etc.: More advanced activation functions can be more stable, and Adam’s adaptive nature can handle them well.

2. Network topologies:

   • Deep CNNs or Transformers with residual connections: Adam’s adaptivity helps with the wide range of gradient magnitudes across many layers.

   • RNNs or LSTMs: These are prone to exploding or vanishing gradients. Adam plus gradient clipping is almost essential for stable training, especially in large sequence tasks.

   • Graph neural networks: Adam is widely used, but one must watch for large graph batch sizes or heavily skewed node degrees, which can lead to gradient spikes.

Are There Recommended Practices for Logging and Visualizing Adam’s Internal Variables During Training?

Yes. Monitoring these variables can provide insights that a simple loss curve might miss:

1. Parameter and Gradient Norms:

   • Track the norm of parameters and their gradients at each iteration or epoch. If the gradient norm frequently spikes, it indicates potential instability.

2. First and Second Moment Norms (exp_avg, exp_avg_sq):

   • Keep a running record of their averages or norms. This can show if the second moment is gradually blowing up or is extremely small.

3. Effective Learning Rate:

   • You can approximate the effective learning rate for each parameter as the ratio of exp_avg to sqrt(exp_avg_sq). Plotting histograms or summary statistics can show whether most parameters are learning or are stuck.

4. Layer-wise Analysis:

   • In complex architectures, log metrics separately for each layer or type of layer (embedding layers vs. convolutional layers, for instance). Some layers may have stable statistics while others are spiking.

In frameworks like PyTorch, hooking into the backward pass or into the optimizer’s step function can gather these statistics. Some practitioners build custom callbacks to log these values to TensorBoard or another tracking system.

Are There Any Theoretical Guarantees for Adam’s Convergence on Non-Convex Problems?

Classical SGD has well-studied theoretical properties, including convergence to critical points under certain assumptions. Adam, being a more complex adaptive method, has additional parameters and conditions. While there are some theoretical results for Adam and Adam-like optimizers, real deep learning tasks are typically highly non-convex, so no universal guarantee of a global optimum exists.

Some key points from research:

• Under specific assumptions (e.g., bounded gradients, properly chosen hyperparameters, diminishing learning rates), Adam can converge to stationary points in convex or quasi-convex problems.

• Non-convex deep neural networks can contain many local minima or saddle points. Adam might quickly find a region of low training loss, but there’s no formal guarantee it’s the best possible region.

• Empirical performance remains the main reason for Adam’s widespread adoption, rather than strict theoretical guarantees.

How Does One Handle the Transition from Adam to a Different Optimizer Mid-Training?

Sometimes you might start training with Adam for rapid progress in the early phases, then switch to SGD (with momentum) later to fine-tune and possibly achieve better generalization. Considerations:

• Reset momentum states: If you switch from Adam to SGD, the first and second moment estimates used by Adam become irrelevant. You’ll need to reset the momentum terms for SGD.

• Learning rate scheduling: When switching optimizers, you might need a short re-tuning or warm-up to avoid a sudden shock to the system.

• Practical approach: Some frameworks allow you to define a schedule or callback that changes the optimizer at a certain epoch. Usually, you’d reinitialize the new optimizer with fresh internal states.

This is sometimes done in large-scale image classification or language modeling tasks. The rationale is that Adam helps you converge quickly in the initial chaotic phases, but a well-tuned SGD might yield a better minimum in the final phases (though this is not always guaranteed).

Can Adam’s Memory Footprint Become a Bottleneck, and How Is This Addressed?

Yes, Adam stores two extra buffers (m and v) of the same size as the parameters. For extremely large models—think billions of parameters—this can be a bottleneck in GPU memory. Potential ways to address this include:

• Shard the optimizer state across multiple GPUs in distributed training. This is handled automatically in some advanced distributed frameworks.

• Use CPU offloading: Move part of the optimizer state to CPU memory, though this can slow down the update step due to data transfer overhead.

• Use memory-efficient variants: Some research focuses on memory-efficient Adam variants that compress or approximate the moment estimates. For instance, 8-bit optimizers can reduce precision for the moment estimates to shrink memory usage with minimal performance impact.

• Hybrid strategies: Keep the second moment in lower precision while the first moment remains in full precision, or apply quantization to the moment buffers.

These techniques help manage large-scale training where memory is limited but the benefits of Adam remain desired.