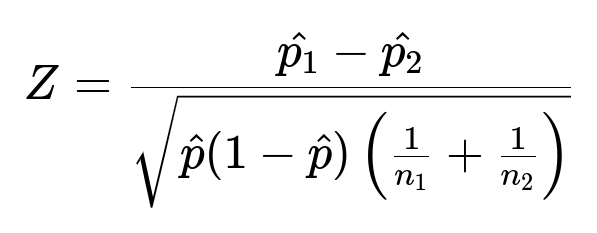ML Interview Q Series: Analyzing A/B Tests with Unequal Groups: Bias vs. Precision Using Z-Tests
Browse all the Probability Interview Questions here.
Suppose you are conducting an A/B test in which one variant is shown to 50K users, while the other variant is shown to 200K users. Do you think the imbalance between group sizes could create a bias that favors or penalizes the smaller group?
Comprehensive Explanation
When performing A/B tests (also known as split tests) with different group sizes (one group has 50K participants, the other has 200K), one frequent question is whether the imbalance by itself introduces any bias. A crucial point to clarify is that “bias” in an A/B testing context typically refers to a systematic error—meaning that the observed effect (e.g., difference in conversion rates) consistently deviates from the true effect due to the way the experiment is designed or conducted. If the assignment of users to each group is random, having a smaller group does not inherently produce bias in the sense of systematically favoring one group over the other. Instead, it simply means that the estimates from the smaller group will have larger variance and less precision, since fewer data points yield wider confidence intervals.
Key Statistical Considerations
It is standard in hypothesis testing to compare sample estimates—like the difference in proportions between two groups—using methods such as a two-proportion z-test. In the case of comparing proportions p1 from n1 participants against p2 from n2 participants, the z-statistic for testing whether the two proportions differ significantly can be formulated around the idea of a pooled proportion, which we often label as p-hat. While we should not fill our explanation with excessive formulas, it is helpful to visualize one core equation in A/B testing.
Where p1-hat and p2-hat are the sample proportions from each group. p-hat is the pooled proportion, typically calculated as the total number of “successes” from both groups divided by the total number of participants in both groups. n1 is the sample size in group 1 (in this scenario, 50K) and n2 is the sample size in group 2 (here, 200K).
This formula illustrates that the main difference when the group sizes are unbalanced is in the standard error term in the denominator. The group with the smaller sample size (50K) contributes more variance on a relative basis, but that effect is properly captured in the test statistic. Hence, no bias is introduced just because n1 < n2.
Why Imbalanced Group Sizes Do Not Intrinsically Cause Bias
Random Assignment: If the process for assigning users to each variant is genuinely random, then each group should be representative of the same underlying population. Even if one group is smaller than the other, that does not imply a systematic shift in user demographics or behaviors unless the randomization process is flawed.
Statistical Frameworks Handle Different Sample Sizes: Confidence intervals and hypothesis testing methods account for group sizes. The bigger group’s proportion estimate is typically more stable, but combining it with the smaller group’s estimate in a correct test statistic (like above) ensures that the difference is evaluated appropriately.
Precision vs. Bias: The smaller group’s result is less precise (wider confidence interval) but not inherently skewed. Bias would arise if the assignment mechanism or data collection systematically favored a certain outcome in one group.
Practical Implications
Although bias is generally not introduced by having unequal group sizes, there are practical considerations:
Statistical Power: With a smaller sample, the power to detect small differences in metrics is lower in that group. However, if your primary focus is the difference between the two variants overall, the test statistic accounts for both sample sizes, and your test can still be valid.
Test Duration: If you planned for both groups to run for the same length of time, the smaller group might need a longer exposure to accumulate enough events to reach the desired statistical power or precision for certain metrics.
Resource Allocation: Sometimes A/B tests use more participants in one variant (for instance, the control version) to preserve user experience or to reduce business risk. As long as randomization is intact, the method remains valid even when one group is smaller.
Potential Follow-Up Questions
Could Unequal Sample Sizes Affect the Reliability of the Results?
Larger sample sizes yield narrower confidence intervals and thus more precise estimates. With 50K vs. 200K, the bigger group’s estimate will be statistically more stable. However, this does not compromise the validity of the A/B test—only the precision. As long as the smaller group still has enough data points to yield a robust estimate of its conversion rate (or whatever metric is being measured), the test conclusions remain reliable. The main impact is that you need to be mindful of potentially larger variance in the smaller group.
What Happens If the Smaller Group Has a Much Higher Variance?
High variance in the smaller group’s metric could lead to broader confidence intervals. In practice, you might see repeated re-runs or re-sampling leading to more fluctuating outcomes for the 50K group. The hypothesis test formula already incorporates this variance, so your test statistic will adjust accordingly. But if the variance is extremely high, you might need to collect more data in that smaller group or consider alternative experiment designs (e.g., sequential testing methods).
How Do You Implement a Two-Proportion Z-Test in Python?
Below is a simple illustrative approach (using SciPy’s built-in functions). Let’s assume you have data on successes for group A (with 50K participants) and group B (with 200K participants):
import numpy as np
from statsmodels.stats.proportion import proportions_ztest
# Suppose group A has 50K participants with 6K conversions
# Suppose group B has 200K participants with 24K conversions
count = np.array([6000, 24000])
nobs = np.array([50000, 200000])
stat, pval = proportions_ztest(count, nobs)
print(f"Z-statistic: {stat}, p-value: {pval}")
In this code:
countholds the number of “successes” (conversions) in each group.nobsholds the total number of observations (participants) in each group.proportions_ztestautomatically applies the appropriate formula.The result gives you a z-statistic and a p-value, telling you whether the difference in proportions is statistically significant.
Are There Scenarios Where Group Size Might Confound the Results?
One scenario might be if the smaller group’s participants are selected from a different user segment, or if the randomization is not truly random—for instance, if there were time-based or geography-based systematic effects. In that case, the smaller group would not be directly comparable to the larger one, and the observed difference might reflect population differences rather than the effect of the variant itself. However, this problem arises from a flawed experimental design, not from the mere fact that the sample sizes differ.
How Would You Address Real-World Constraints That Lead to Unequal Group Sizes?
Stratified Sampling: You could ensure each relevant subgroup or demographic is proportionally represented in both variants to maintain comparability.
Weighted Analysis: In some advanced scenarios, you might weight users from different segments if the segments were imbalanced across the two variants.
Sequential Testing: If the test must initially be skewed to one group for business reasons, a sequential approach can help you terminate the test early if the difference is large and stable.
Overall, different sample sizes in A/B tests do not, by themselves, introduce bias. They simply affect the precision and power of the test. By using proper randomization and analytical methods, you can still obtain an unbiased estimate of the difference in performance between the two variants.
Below are additional follow-up questions
How Would You Handle a Situation Where the Smaller Group Produces Very Few Conversions?
One subtle challenge arises if the smaller group barely produces any positive “success” events (like conversions). This might happen if the product feature doesn’t resonate with that subset of users or if the overall conversion rate is extremely low. When the number of successes is very small, the normal approximation in a z-test can break down, potentially causing a distorted view of the confidence interval. Here are some strategies:
Use Alternative Statistical Methods: Instead of a z-test that relies on normal approximations, consider using exact tests such as Fisher’s exact test, which is especially suitable for small count data.
Combine Observations or Extend the Test: If feasible, run the experiment longer or ensure the smaller group receives more traffic. This approach increases the chance of observing more conversions, mitigating issues from small sample counts.
Perform Bayesian Analysis: Bayesian methods can handle low-count scenarios more gracefully, as prior distributions can help stabilize estimates.
A real-world pitfall is letting the test conclude too early when the smaller group lacks enough success events, thereby creating a misleading interpretation of results.
What If You Discover Post-Hoc That the Smaller Group Consists of a Different Demographic?
Sometimes, after running an A/B test, you might uncover that the smaller group systematically differed from the larger group (e.g., the smaller group was mostly from a certain region, device type, or user segment). This can happen if randomization was unintentionally circumvented by user behavior or marketing decisions. The potential pitfalls here include:
Failure of Randomization: The differences in user demographics mean you are effectively testing two different populations, which invalidates many assumptions of standard hypothesis tests.
Adjusting Your Analysis: You could use stratification or covariate adjustment if the demographic variable is known. For instance, segment your analysis by user country or device type and test within each segment.
Re-run the Experiment: If the disparity is too large and cannot be corrected analytically, you might have to redesign the randomization or re-run the test to ensure balanced representation.
The practical lesson is to track user attributes carefully and verify random assignment from the outset to avoid biasing the results due to an unexpected population mismatch.
Could External Events Unequally Impact the Smaller Group?
In the real world, unforeseen external factors may influence only a specific subset of users (e.g., a marketing campaign or a temporary regional outage). If the smaller group happens to be disproportionately affected by these events, the results of the experiment could be skewed. Important considerations include:
Monitoring External Factors: Keep track of marketing pushes, website downtime, or region-specific issues. If these factors overlapped heavily with the smaller group, the resulting performance might not reflect the product’s actual effect.
Time-Based Partitioning: If a campaign ran in a short window that mostly included the smaller group, you can segment the data by time period to see if the discrepancy still holds outside that window.
Sensitivity Analysis: Remove the data from the affected period or region and re-check the difference in metrics. If removing these data points changes the conclusion, you know the external event confounded the test.
The key pitfall is attributing changes in performance to the product change, when in fact the real cause might be an external event hitting one subset more significantly.
What If the Smaller Group’s Results Fluctuate Heavily Over Time?
Another nuanced situation involves the smaller group exhibiting large swings in daily or weekly metrics, while the larger group remains relatively stable. You should consider:
Statistical Process Control: Track the conversion metrics or performance metrics over time (e.g., daily or weekly) for both groups. Check whether there are out-of-control signals in the smaller group.
Check for Underlying Sub-Segments: Within the smaller group, a few “heavy users” might disproportionately affect results if they appear sporadically. Investigating user-level data can unveil whether outliers drive the fluctuations.
Lengthen the Test Window: Extending the experiment duration can smooth out day-to-day variance. The smaller the group, the longer it often requires to stabilize estimates around a mean.
Without addressing volatility, you might draw incorrect conclusions about which variant is truly better, because short-term spikes or drops in a small sample can mask the long-run average effect.
How Do You Handle a Scenario Where Your Main Metric Is Not a Simple Conversion Rate But a Continuous Value?
A/B testing often focuses on binary metrics (converted vs. not converted). But in many cases—especially in revenue or engagement analyses—the metric is a continuous variable (e.g., average order value, session length). With unequal group sizes, you need to consider:
Parametric vs. Nonparametric Tests: If the continuous metric is reasonably normally distributed (or if you have enough data for the Central Limit Theorem to hold), you might use a t-test. If the distribution is heavily skewed, you could consider a nonparametric test (like the Mann-Whitney U test) or transform the metric (e.g., using a logarithmic transform).
Variance Considerations: The group with fewer samples will have a less precise estimate of mean or median, and possibly more susceptibility to outliers. Be sure to investigate variance in each group separately.
Trimming or Winsorizing: If large outliers dominate the smaller sample, you might trim extreme values or apply winsorization to reduce their impact. Always check if these outliers are legitimate data points or data errors.
A major pitfall is applying a simple proportion test methodology to a continuous metric or ignoring the impact of outliers in the smaller group. This can lead to significant misinterpretation of results.
What If the Experiment Is So Unbalanced That the Smaller Group Represents Less Than 5% of the Total?
Severe imbalance, like 5% of traffic going to variant A and 95% to variant B, can be intentional for risk mitigation or product rollout strategies. To manage the extreme imbalance:
Power Analysis: Conduct a power calculation to ensure the minimal sample (the smaller group) is large enough to detect a meaningful difference. Even if 5% is allocated, you might need a longer test duration.
Sequential vs. Fixed-Horizon Tests: With a highly skewed allocation, you might adopt sequential testing methods that allow you to stop the test once you’ve reached a statistically valid conclusion, especially if the smaller group exhibits strong evidence for or against an effect early on.
Potential Ethical/Business Constraints: Sometimes, rolling out a big new feature to only 5% of users is a safer approach, but it prolongs the time needed to conclude the test. Plan carefully so you don’t end up in an “undecidable zone” because you never gathered enough data from the smaller group.
The main pitfall is underestimating how much data is required in the minority group to confidently differentiate from the majority group.
How Do You Deal with Running Multiple A/B Tests Simultaneously with Different Group Ratios?
In a real-world environment, you might have multiple experiments running in parallel, each potentially dividing traffic differently. If your variant for one experiment ends up in the smaller group for another experiment, cross-experiment interference may arise. To handle this:
Mutually Exclusive Groups: You might run each experiment on a disjoint subset of users (e.g., 10% of traffic dedicated to experiment A, 10% to experiment B, 80% control), ensuring no overlap in users. However, this approach can greatly reduce overall sample sizes.
Factorial Designs: If you expect that multiple variants can co-exist without interfering, you might use a factorial design. That means a user can be simultaneously in variant A of one experiment and variant B of another, but you track combined outcomes carefully to isolate separate and interaction effects.
Holistic User-Level Randomization: A randomization system that globally assigns users to test cells ensures each experiment’s group assignments are truly random. You then measure metrics for each experiment, controlling for exposure to other simultaneous variants if needed.
The edge case to watch out for is an unforeseen interaction between two experiments. If an experiment modifies the user interface in ways that overshadow or block the effect measured in another experiment, the results of both tests might be invalidated.