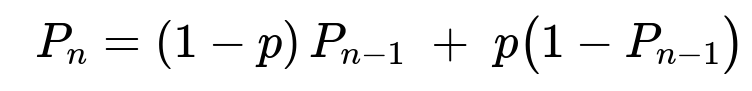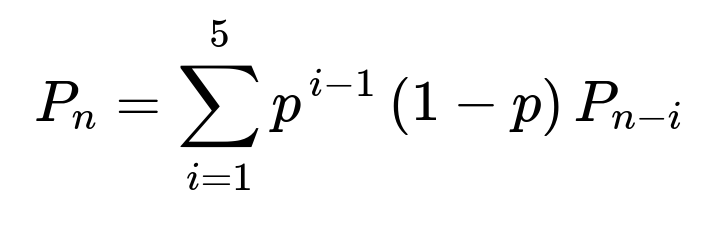ML Interview Q Series: Analyzing Biased Coin Tosses: Recursive Solutions for Parity and Run Constraints
Browse all the Probability Interview Questions here.
A biased coin is tossed repeatedly. The probability that a toss of the coin results in heads is p with 0 < p < 1.(a) Give a recursion for the probability that the total number of heads after n tosses is even.(b) Give a recursion for the probability that a sequence of n tosses does not show five or more consecutive heads.
Short Compact solution
For part (a), let An be the event that the total number of heads after n tosses is even, and define Pn as the probability of An. Consider whether the first toss is tails (probability 1 - p) or heads (probability p). This leads to the recursion
For part (b), let An be the event that a sequence of n tosses does not have five or more consecutive heads, and define Pn = P(An). We split the possibilities for the first few tosses by defining disjoint events that capture how the sequence starts. In particular, if the sequence begins with exactly i - 1 heads followed by a tail (for i = 1 to 5), the probability is p^(i-1)(1 - p). If the sequence starts with five heads (event B6), then the probability of An given that start is 0, because the requirement is violated immediately. Combining these cases gives:
for n ≥ 5, with initial conditions P0 = P1 = P2 = P3 = P4 = 1.
Comprehensive Explanation
Understanding part (a):
We want the probability that the number of heads after n tosses is even. Denote that probability by Pn. If the first toss is tails (which happens with probability 1 - p), the parity of the number of heads does not change; so if we had an even number of heads before, we remain in the “even” case, and if we had an odd number before, we remain in the “odd” case. Conversely, if the first toss is heads (with probability p), then the parity flips from even to odd or from odd to even.
From these observations, you can write: Pn = (1 - p)Pn-1 + p(1 - Pn-1).
This is a simple linear recurrence. In more detail:
If the previous (n−1)-toss sequence had an even number of heads, then to keep it even after the nth toss, the nth toss must be tails.
If the previous sequence had an odd number of heads, then to obtain an even total, the nth toss must be heads.
Initial condition: When n = 0 (no tosses), we consider the count of heads to be 0, which is even, so P0 = 1.
Solving the recurrence can be done by standard techniques for first-order linear difference equations. The closed-form solution turns out to be: Pn = 1/2 + (1/2)(1 - 2p)n.
The term (1 - 2p)n decays to 0 as n grows large (for any 0 < p < 1), so Pn tends to 1/2 for large n. This also matches intuition: in the long run, we expect half the time the number of heads to be even, half the time to be odd.
Understanding part (b):
We want the probability that no run of five or more consecutive heads appears in n tosses. Denote this probability by Pn. If the sequence is short (n < 5), no run of five consecutive heads can appear, so P0 through P4 are all 1.
For n ≥ 5, think about how the sequence might start:
If it starts with (i−1) heads followed by a tail, for i in {1,2,3,4,5}, then this occurs with probability pi-1(1 - p). After those i tosses, we are free to continue any valid sequence of length n−i with no run of five heads. That continuation probability is Pn-i.
If it starts with five heads (event B6), then we have already violated the condition of “no five or more consecutive heads,” so the probability of satisfying An after starting with five heads is 0.
Hence the total probability is the sum of all the ways we can start with fewer than five consecutive heads (i.e., from 0 to 4 heads in a row), each scenario multiplied by the conditional probability that the remainder of the sequence also avoids five in a row:
Pn = ∑i=1..5 pi-1(1 - p) Pn-i, for n ≥ 5.
With the initial values P0 = P1 = P2 = P3 = P4 = 1, we can compute Pn for any n ≥ 5 by building up from smaller n.
Because a run of k consecutive heads can be handled with similar logic, this method easily generalizes if we wanted to forbid, say, six or more heads in a row, although the recursion would then sum up to i in {1..k}.
Implementation note: One can implement these recursions in Python or any other language quite easily, since each Pn depends on earlier values. For example:
def prob_even_heads(n, p):
# part (a)
P = [0]*(n+1)
P[0] = 1 # P0 = 1
for i in range(1, n+1):
P[i] = (1 - p)*P[i-1] + p*(1 - P[i-1])
return P[n]
def prob_no_five_in_a_row(n, p):
# part (b)
P = [1]*max(n+1, 5) # ensure length at least 5
# Base cases
P[0] = 1
P[1] = 1
P[2] = 1
P[3] = 1
P[4] = 1
# Recurrence
for i in range(5, n+1):
P[i] = 0
for j in range(1, 6):
P[i] += (p**(j-1)*(1-p))*P[i-j]
return P[n]
This dynamic programming approach simply follows the recurrences directly.
Possible Follow-Up Questions
Why does Pn tend to 1/2 for part (a)?
As n grows, the factor (1 - 2p)n goes to 0 for 0 < p < 1 because |1 - 2p| < 1. Therefore, the closed-form solution Pn = 1/2 + (1/2)(1 - 2p)n approaches 1/2. Intuitively, in a large number of independent flips, you would expect heads to be roughly half of them, so the parity should be about evenly split.
How can we extend part (b) to the case of k consecutive heads?
If we do not want to see k or more consecutive heads, we define a similar recursion but consider events that the first i - 1 flips are heads followed by a tail (for i from 1 to k−1). If the sequence starts with k heads, it fails immediately. Thus, the recursion for Pn would be:
Pn = ∑i=1..k-1 pi-1(1 - p) Pn-i.
The initial conditions would be all 1 for n < k.
What is a potential pitfall in computing Pn if n is large?
For extremely large n, repeated multiplication by p or (1 - p) can cause floating-point underflow if p is very small or very large. Also, computing (1 - 2p)n for large n might cause numerical issues if |1 - 2p| ≈ 1. One can sometimes mitigate these issues by using logarithms or other numerical techniques.
How would you verify these formulas empirically?
You could run a simulation:
Generate many independent Bernoulli(p) coin-toss sequences of length n.
Compute the fraction of trials where the number of heads is even (for part a).
Compute the fraction of trials that do not contain at least five consecutive heads (for part b).
Compare these empirical fractions with the theoretical predictions from the recurrences.
Could these concepts be applied to Markov chains?
Yes. Each of these recurrences effectively describes a Markov chain on a small state space. For part (a), the “state” is simply whether we are in “even” or “odd.” For part (b), the state can be the count of how many consecutive heads you currently have, capped at some maximum.
Are these recurrences relevant in real-world machine learning tasks?
Potentially. Modeling processes that depend on “event counts mod 2” or “forbidden runs” is a known technique in reliability, quality control, or in sequence modeling tasks where certain patterns (e.g., runs of certain events) are disallowed or must be tracked. They also come up in sequence generation constraints in areas such as language modeling or anomaly detection, especially where one wants to avoid repeating certain tokens too many times.
These detailed explanations and potential follow-ups demonstrate the reasoning behind each recursion, highlight their range of validity, and show how one might generalize or implement them in practice.
Below are additional follow-up questions
What happens if p is very close to 0 or very close to 1? Do the recurrences still work?
If p is extremely small (near 0), the probability of getting heads in any toss is very low. For part (a), in most sequences, heads will be rare, so the term (1 - 2p)^n in the closed-form might be quite close to (1)^n = 1 if p is extremely small (but not exactly 0, of course). However, this factor still decays toward 0 for p strictly between 0 and 1, so P_n converges to 1/2 in the long run. If p is extremely large (close to 1), the same logic applies: |1 - 2p| < 1 still, so the recurrences are valid. In actual computation, floating-point underflow or overflow could occur if p is so close to 0 or 1 that p^n is below machine precision or (1-p)^n is similarly tiny. One practical pitfall is that if p is exactly 0 or 1 (excluded by the 0 < p < 1 assumption), the formula breaks down because we end up with deterministic outcomes in which heads or tails are guaranteed on every toss.
For part (b), if p is very small, it becomes extremely unlikely to see runs of five heads. The recursion remains correct, but P_n will be close to 1 for all reasonable n. Conversely, if p is near 1, almost every toss is heads, so once n exceeds 5, it becomes highly probable to get a run of five heads almost immediately, making P_n approach 0. Numerically, you must be careful with exponentiation of very small or very large probabilities when computing terms like p^(i-1).
How can we adapt part (a) if we want the probability that the total number of heads is exactly k rather than just even?
The event “number of heads after n tosses is exactly k” is a classic Binomial(n, p) probability. So from first principles, we have P(X = k) = C(n, k) * p^k * (1 - p)^(n-k). However, if you wanted to build a recursion to compute P(X = k) directly (instead of using the closed-form binomial expression), you could note that:
From step n-1 to step n, you can either add a head (with probability p) or a tail (with probability 1 - p).
P(X = k, n tosses) = p * P(X = k-1, n-1 tosses) + (1 - p) * P(X = k, n-1 tosses).
This recursion is typical for a binomial distribution. The edge cases are P(X = 0, 0 tosses) = 1 and P(X = k, 0 tosses) = 0 for k > 0. A potential pitfall is indexing errors (e.g., forgetting that you need k > 0 if you want to add a head) and handling boundary conditions carefully when k = 0 or k = n.
How would the solution approach change if coin tosses were not independent?
Both recurrences depend crucially on the independence of tosses. For part (a), the simple parity-flip argument—“if the nth toss is a head, parity flips; if it’s a tail, parity stays the same”—relies on independence and a fixed probability p for heads at each toss. If the coin had memory (e.g., a Markov chain with transitions that depend on the previous result), we couldn’t simply say the probability of a head is p each time.
For part (b), the logic that “we start with i - 1 heads and then a tail, which has probability p^(i-1)(1 - p), and continue” also depends on each flip being identically distributed with probability p of heads. In the dependent scenario, the chance of seeing a head or tail might vary based on the sequence so far, so the recursion would need to incorporate the state representing how many consecutive heads we currently have (plus any additional memory). This approach can still be done with a Markov chain, but p is replaced with transition probabilities that depend on the chain’s states. The biggest pitfall is failing to update the recurrence to reflect the new dependency structure—leading to incorrect probabilities if one tries to apply the old formula.
Could generating functions be used to solve or check the recurrences?
Yes. For part (a), the generating function for the number of heads in n tosses of a biased coin is ( (1 - p) + p z )^n, and one can separate out the even-power terms to find the probability that the exponent of z is even. You would end up with the same result (1/2 + 1/2 (1 - 2p)^n). Generating functions simply provide an alternative viewpoint, which can be used to sum or isolate certain terms (e.g., even vs. odd exponents).
For part (b), generating functions become more complex because you’re tracking a pattern-avoidance constraint (no run of five heads). While there is a known combinatorial generating function approach for counting sequences that avoid certain runs, it’s a bit more involved than the direct recursion. A pitfall here is mixing up ordinary generating functions (OGFs) versus exponential generating functions (EGFs), or making mistakes in counting sequences that appear valid but actually hide a run of five heads. Careful combinatorial arguments or direct dynamic programming is usually simpler to implement in code.
How would you handle partial observations in the sequences?
If some of the tosses are unknown or lost (for example, you only observe a subset of tosses), then the calculation of “the number of heads is even” or “there are no five consecutive heads” must condition on partial information. Part (a)’s direct recursion won’t hold if you do not know some toss outcomes. Instead, you might incorporate the missing tosses as random variables with some known or assumed distribution, then average over all possible completions of those missing data. For part (b), the maximum consecutive heads could be influenced by whether the missing tosses might contain a run of heads. A subtlety is bounding the number of consecutive heads in the presence of uncertain outcomes: either you treat them as random and incorporate them in a more complicated state-based approach, or you interpret missing data as “unknown” and only measure guaranteed occurrences of runs. The major pitfall is incorrectly ignoring or double-counting possibilities for the missing tosses, leading to an over- or underestimation of P_n.
Are there purely combinatorial (enumerative) methods for part (b)?
Yes. One can try to directly count the number of sequences of length n that do not contain five or more consecutive heads and then divide by the total number of possible sequences (2^n if it were an unbiased coin, or just 1 for the combinatorial shape, but you’d weight them by p^(# heads) (1-p)^(# tails) for the biased case). However, enumerating all valid sequences is typically O(2^n), which grows exponentially. A more refined combinatorial approach can do a dynamic count by states that represent how many consecutive heads appear at the end of the partial sequence. This is effectively the same logic as the recursion:
P_n = sum over i=1..5 of p^(i-1)(1-p) P_{n-i}.
So in practice, dynamic programming or direct recursion is often simpler. The pitfall in enumerative approaches is complexity: naive enumeration is infeasible for large n.
How would we combine conditions from part (a) and part (b)? For example, the probability that we have an even number of heads AND no run of five heads?
Combining the two constraints means we want sequences with even total heads that also do not contain five or more consecutive heads. One approach is to expand the state space in a dynamic programming scheme. Each state might be characterized by:
The number of consecutive heads so far (0 through 4), and
The parity of the count of heads (even or odd).
Then you have transitions depending on whether the next toss is a head or a tail. If you ever reach 5 consecutive heads, you fail the condition. If you get to n tosses, you check if the parity is even. The pitfall is that the state machine becomes more complex, but it’s still finite and manageable. Once the states are well-defined, you can compute the probability by multiplying appropriate transition probabilities. Neglecting to track both parity and consecutive heads can lead to partial or incorrect answers.
Can we find the expected time until we first see five consecutive heads?
That’s a different but related problem. The expected time to first occurrence of a run of five heads (a stopping time problem) usually involves a Markov chain approach, where the chain’s state is how many consecutive heads have occurred so far (0 to 5). Once you reach 5, you stop. This leads to a system of linear equations for the expected time from each state:
E_0 = 1 + (1 - p) E_0 + p E_1, E_1 = 1 + (1 - p) E_0 + p E_2, ... E_4 = 1 + (1 - p) E_0 + p E_5, E_5 = 0.
Solving this system gives the expected time to see five consecutive heads for the first time, starting from state 0. One subtlety is that the expected time might be quite large if p is small (because it is unlikely to get a single head in each toss), yet the method still works. A pitfall is that if you rely on direct simulation to estimate it, you may need a large number of simulated sequences, especially if p is small, because it can take a very long time to see five heads in a row.
How large should a simulation sample be for empirical estimates of these probabilities?
When running a Monte Carlo simulation to estimate probabilities such as “an even number of heads after n tosses” or “no run of five or more heads,” you typically want enough samples to achieve a confidence interval that is sufficiently narrow for your purposes. If you’re aiming for an error margin of (for instance) plus or minus 0.01, you might use classic variance-based confidence intervals for Bernoulli estimates. A rule of thumb is that you need around 1/(error^2) independent samples to get a standard error near the target. For smaller p or complicated constraints like “no run of five heads,” you might see more variance in the estimator, so you’d need more samples. One pitfall is failing to account for correlated sequences (if you run multiple partial sequences in a naive way) or misjudging the number of iterations needed, leading to inaccurate probability estimates.