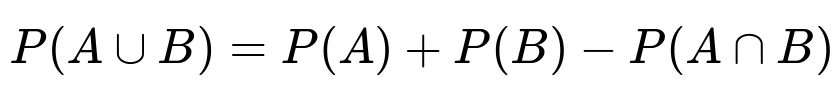ML Interview Q Series: Analyzing Language Enrollment Overlap Using Conditional Probability Principles.
Browse all the Probability Interview Questions here.
In a high school class, 35% of the students take Spanish as a foreign language, 15% take French as a foreign language, and 40% take at least one of these languages. What is the probability that a randomly chosen student takes French given that the student takes Spanish?
Short Compact solution
Let A be the event that a student takes Spanish, and B be the event that a student takes French. We know P(A) = 0.35, P(B) = 0.15, and P(A ∪ B) = 0.40. Applying the basic formula for the union of two events:
we get 0.40 = 0.35 + 0.15 - P(A ∩ B), so P(A ∩ B) = 0.10. Then, the desired probability P(B|A) = P(A ∩ B) / P(A) = 0.10 / 0.35 = 2/7.
Comprehensive Explanation
First, define the events clearly. Let A be the event “student takes Spanish” and B be the event “student takes French.” We have three core probabilities:
P(A) = 0.35, meaning 35% of the students take Spanish.
P(B) = 0.15, meaning 15% of the students take French.
P(A ∪ B) = 0.40, meaning 40% of the students take at least one of these languages (Spanish or French).
The probability that a student takes both Spanish and French, denoted P(A ∩ B), can be found from the formula for the union of two events:
Placing the given values into this formula:
0.40 = 0.35 + 0.15 - P(A ∩ B)
Rearranging to solve for P(A ∩ B):
0.40 = 0.50 - P(A ∩ B)
so
P(A ∩ B) = 0.50 - 0.40 = 0.10.
Hence, 10% of the students take both Spanish and French.
The question asks for the conditional probability that a randomly chosen student takes French given that the student takes Spanish, which is denoted P(B|A). By definition:
We already found P(A ∩ B) = 0.10, and P(A) = 0.35. Substituting these values:
P(B|A) = 0.10 / 0.35 = 2/7.
Numerically, 2/7 is approximately 0.2857, or 28.57%.
The reasoning behind this is straightforward once one recalls that the union of two events is P(A) + P(B) minus any overlap between the events (i.e., P(A ∩ B)). Then, conditional probability simply measures the proportion of event A’s occurrence that also satisfies event B.
Follow-up question: Are the events Spanish and French independent?
Two events A and B are independent if P(A ∩ B) = P(A)*P(B). Here, P(A)P(B) = 0.350.15 = 0.0525. However, we have P(A ∩ B) = 0.10. Since 0.10 is not equal to 0.0525, the events are not independent. In other words, there appears to be a higher overlap between Spanish and French than would be expected by chance alone, indicating that students who take Spanish might be more likely to also take French (or vice versa) than if the two languages were chosen entirely independently.
Follow-up question: What is the difference between P(A|B) and P(B|A)?
P(A|B) is the probability that a randomly chosen student takes Spanish given that the student takes French. P(B|A) is the probability that a randomly chosen student takes French given that the student takes Spanish. These two probabilities can be quite different unless A and B are symmetric in some sense (e.g., if the two events are equally likely or perfectly correlated). Numerically:
We already have P(B|A) = 2/7 ≈ 0.2857.
P(A|B) = P(A ∩ B) / P(B) = 0.10 / 0.15 = 2/3 ≈ 0.6667.
This makes sense because among the 15% who take French, 10% are also in Spanish, so two-thirds of the French students also take Spanish. Meanwhile, among the 35% who take Spanish, only 10% also take French, which is roughly 28.57%.
Follow-up question: Can we illustrate these percentages in a simple breakdown?
Yes. Since P(A ∩ B) = 0.10, we can list the proportions in a Venn diagram style (in decimal form):
Spanish only: P(A) - P(A ∩ B) = 0.35 - 0.10 = 0.25
French only: P(B) - P(A ∩ B) = 0.15 - 0.10 = 0.05
Both Spanish and French: 0.10
Neither Spanish nor French: 1 - P(A ∪ B) = 1 - 0.40 = 0.60
These values sum to 1. We can check: 0.25 (Spanish only) + 0.05 (French only) + 0.10 (both) + 0.60 (neither) = 1.0.
Follow-up question: How could this be tested programmatically in a quick simulation?
One could simulate a population of students with these probabilities. For instance, if we have a large number of students (say 1 million), we assign them to “take Spanish,” “take French,” both, or neither, in proportions consistent with the above breakdown. Then we can compute the conditional probability numerically and see if it matches 2/7.
A simple Python snippet for demonstration:
import numpy as np
num_students = 10_000_000
# The breakdown derived above
p_spanish_only = 0.25
p_french_only = 0.05
p_both = 0.10
p_neither = 0.60
students = np.random.choice(
["spanish_only", "french_only", "both", "neither"],
p=[p_spanish_only, p_french_only, p_both, p_neither],
size=num_students
)
# Probability that a student takes French given that they take Spanish
# i.e. from the set {spanish_only, both}, how many are 'both'?
spanish_indices = (students == "spanish_only") | (students == "both")
both_indices = (students == "both")
observed_p_B_given_A = both_indices.sum() / spanish_indices.sum()
print("P(French | Spanish) ~", observed_p_B_given_A)
This simulation should yield a value close to 0.2857, confirming the theoretical result.
Follow-up question: What if P(A ∪ B) were greater than P(A) + P(B)?
If P(A ∪ B) were ever reported as a value greater than P(A) + P(B), it would indicate an inconsistency, since for any two events A and B, P(A ∪ B) cannot exceed P(A) + P(B). In fact, the union formula P(A ∪ B) = P(A) + P(B) - P(A ∩ B) ensures P(A ∪ B) ≤ 1, and if the data suggested otherwise, it would be an error in the provided probabilities or a misunderstanding of how the events are defined.
Below are additional follow-up questions
If other foreign languages are also offered, how might that affect these probabilities?
When the problem states that 35% take Spanish and 15% take French, it is implicitly referring to Spanish and French as the only foreign languages. In reality, there could be students who take German, Chinese, or any other language. The presence of additional languages doesn't invalidate the calculations directly, provided the percentages given refer specifically to Spanish and French enrollments. However, the challenge arises if the events A (“takes Spanish”) and B (“takes French”) are not mutually exclusive with taking other languages (e.g., a student might take Spanish, French, and possibly German). In that case:
The union P(A ∪ B) accounts for students who take Spanish, French, or both, but not necessarily excluding students taking a third language.
Overlapping enrollments with other languages can increase or decrease the probability that a student in A also ends up in B, depending on curriculum constraints or schedules.
A potential pitfall is that if the school’s data lumps all “foreign language students” into a single group without careful categorization, then the raw percentages for Spanish or French might be misleading or incorrectly tallied. For instance, some might list “Students taking any foreign language” as 40% and interpret that incorrectly as P(A ∪ B) if other languages exist. Hence, clarity in definitions becomes crucial: we want the proportion that specifically takes Spanish or French (or both), not just any foreign language.
How does the Law of Total Probability apply if we introduce additional grouping variables?
The Law of Total Probability typically states that for an event A, if we have a partition of the sample space into events X1, X2, …, Xn, then:
In this scenario, we might introduce partitioning variables such as “grade level,” “honors vs. regular track,” or “class schedule constraints.” Each X_i would represent a category (e.g., X1 = “freshman,” X2 = “sophomore,” and so on). Then we could write:
P(A) = P(A|freshman)*P(freshman) + P(A|sophomore)*P(sophomore) + …
Similarly, we could use this approach to break down P(A ∩ B) by each partition, or to compute the conditional probability P(B|A) in a more granular way:
P(B|A) = Σ [ P(B|A, X_i) * P(X_i | A) ] over all i.
This deeper breakdown might reveal that certain subgroups are more or less likely to take both languages (e.g., maybe juniors have a higher overlap than seniors). A pitfall arises if we assume uniform probabilities across different grade levels or tracks, ignoring the variability in scheduling options.
Could scheduling constraints create biases that affect these probabilities?
In many real-world educational settings, students may only be allowed to take two foreign languages if there is room in their schedules and if their academic track permits it. This practical constraint can artificially inflate or deflate the overlap P(A ∩ B). For instance:
If the schedule has limited slots, it could discourage double enrollment, making P(A ∩ B) smaller.
Conversely, a special track (e.g., an advanced language program) might encourage students to take multiple languages, increasing P(A ∩ B).
In interview settings, an interviewer might test whether you have considered real-world constraints. If you assume no scheduling conflicts, you might incorrectly claim the events are “almost independent.” A robust answer acknowledges these structural limitations and notes that they can systematically shift the probabilities observed in actual data.
How might missing or imperfect data about student enrollments affect our estimates?
Real datasets can have missing rows (e.g., some students not reporting which language they take), or inaccurate record-keeping:
If certain students never filled out the language-preference form, we might underestimate P(A), P(B), or both.
If double counting occurs in the data (e.g., a student listed in Spanish once and in French once but not flagged as the same student), we might erroneously inflate P(A ∩ B).
From a data science perspective, if we suspect data quality issues, we might:
Perform data cleaning or deduplication to ensure each student has a single consolidated record.
Estimate the amount of missing data and possibly impute or set bounds on P(A ∩ B).
This real-world scenario underscores that the neat formula P(A ∩ B) = P(A) + P(B) - P(A ∪ B) holds only if the data are accurately representing the true subsets.
What if the question asked about P(A|B^c) or P(B^c|A^c), where B^c is the complement of B?
We typically compute conditional probabilities such as P(B|A) or P(A|B), but sometimes interviewers will flip the question to see if you can handle complements:
P(B^c|A): Probability that a student does not take French, given that they take Spanish.
P(A|B^c): Probability that a student takes Spanish, given that they do not take French.
These variants can be computed using relationships like:
P(B^c|A) = 1 - P(B|A)
and similarly,
P(A|B^c) = P(A ∩ B^c) / P(B^c).
In our situation:
We already know P(B|A) = 2/7, so P(B^c|A) = 1 - 2/7 = 5/7.
B^c means the student does not take French, so P(B^c) = 1 - 0.15 = 0.85. Then A ∩ B^c means “takes Spanish but not French,” which is 0.25, and so P(A|B^c) = 0.25 / 0.85 ≈ 0.2941.
A pitfall would be mixing up complements and incorrectly subtracting from the wrong base probability, so it’s important to carefully keep track of the sets and complements.
How do we interpret these probabilities if we consider a Bayesian perspective?
In a Bayesian setting, P(B|A) can be thought of as updating our belief about whether a student takes French once we know the student takes Spanish. The prior probability that a student takes French is 0.15. Upon learning that the student takes Spanish, we update this probability to 0.10/0.35 = 2/7. That is a posterior probability in Bayesian terms. One might ask:
What if we had a “prior” belief about how language enrollments are distributed, and then we observe new data from a random sample of students?
Could that shift our estimate of P(B|A)?
The Bayesian perspective emphasizes that these probabilities can be dynamically updated as new information (or new enrollment data) becomes available. A subtle pitfall is assuming the distribution remains constant year after year without checking whether the data has changed (for instance, if a new immersion program drastically increases the overlap).
How might demographic factors or student interests confound the correlation between Spanish and French enrollment?
Factors such as academic motivation, cultural background, or teacher recommendations might mean that certain students are more likely to take multiple languages. This can cause a confounding effect. For example, high-achieving students may tend to enroll in more challenging academic programs, which might include both Spanish and French. Meanwhile, other students might opt for only one language. This non-random assignment leads to a correlation in the data. In an interview, an employer may want you to recognize that correlation does not imply causation. Students who take Spanish do not automatically cause themselves to also take French. Instead, an underlying factor (like strong interest in languages) may drive them to choose both.
A pitfall is to conclude that “taking Spanish causes students to also take French” purely from seeing a high P(A ∩ B). Without controlling for these confounders, one cannot draw strong causal inferences.
How could we extend this problem to multiple languages using probabilities of three-way intersections?
If the school offered three languages (say Spanish, French, and German), we would need the probabilities of each language individually and each pairwise intersection, along with the triple intersection P(A ∩ B ∩ C). For instance, we might define:
A: takes Spanish
B: takes French
C: takes German
Then we could still use the principle of inclusion-exclusion for three sets:
If the interviewer wants you to generalize your knowledge, the concept extends naturally but becomes more cumbersome. You’d need more data points (or assumptions) to solve for all intersections. A common pitfall is forgetting to add back the triple intersection if it exists, which can lead to double subtraction errors in the union formula.
How could we measure the “strength” of the relationship between taking Spanish and taking French?
While P(B|A) is a direct conditional probability, one might explore measures akin to correlation or association. For instance, we can look at:
The Relative Risk = P(B|A) / P(B), which tells us how many times more likely a student taking Spanish also takes French, compared to the baseline French-taking probability. In our case, that would be (0.10/0.35) / 0.15 = (2/7) / 0.15. A ratio of >1 implies there is a positive association.
The Odds Ratio = [P(A ∩ B)/P(A^c ∩ B^c)] / [P(A ∩ B^c)/P(A^c ∩ B)] if we consider events in a 2x2 table context. This is common in statistics (particularly in medical or social science studies) to gauge the strength of association between two categorical variables.
A potential pitfall is mixing up correlation-based metrics with conditional probabilities and trying to interpret them interchangeably. Conditional probability focuses on “given an event, how likely is another?” whereas a correlation-based measure tries to gauge how strongly two variables move together, often without specifying direction.
How could an online learning platform use these probabilities to recommend additional courses to students?
If a platform sees that a student is enrolled in Spanish, it can compute P(B|A)—the likelihood they’d also be interested in French—and use that to suggest a French class. This is analogous to the “item-based collaborative filtering” approach where if a user buys or likes one item, the system recommends a related item. However, a pitfall in real-world recommendation systems is that correlation does not always translate into personal relevance. Just because many Spanish students also enroll in French doesn’t guarantee a specific Spanish student will want to do so. Systems often rely on more fine-grained data like progress metrics, preference surveys, or demographic profiles to refine recommendations.