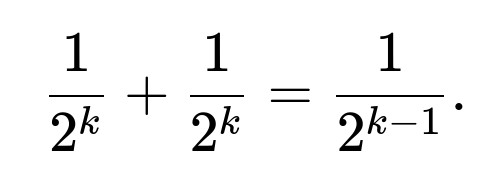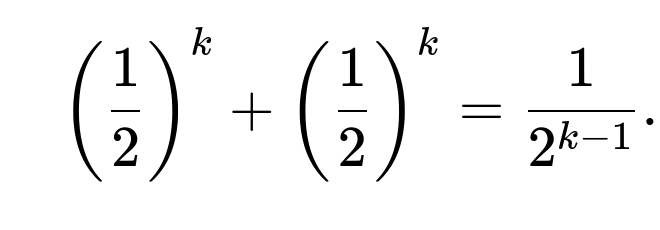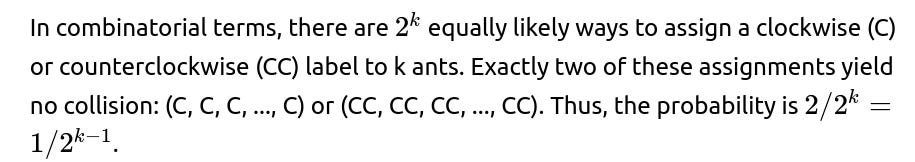ML Interview Q Series: Ants on a Polygon: Calculating Collision Avoidance Probability
Browse all the Probability Interview Questions here.
Three ants are placed at the corners of an equilateral triangle. Each ant chooses at random to walk clockwise or counterclockwise along the sides. What is the probability that none of them will ever meet? Moreover, if k ants are arranged at the vertices of an equilateral polygon, how does this probability extend?
Short Compact solution
Generalizing to k ants on an equilateral k-gon, the same reasoning applies: the ants never collide only if they all choose clockwise or all choose counterclockwise. Each individual’s choice is 1/2, so the total probability of no collision is
Comprehensive Explanation
The Core Reasoning
When ants start at the corners of a regular geometric shape such as an equilateral triangle (or a k-sided regular polygon), the only circumstance in which they never collide is that they must “chase” each other indefinitely around the perimeter without ever coming face-to-face. This perpetual avoidance can happen only if all ants pick the same direction. In a triangle, if even one ant chooses the opposite direction from the other two, at least one collision is inevitable.
To see why collisions are certain in any other situation, observe that if at least two ants choose different directions, they will eventually converge on a shared vertex or intersect on an edge. In simpler terms, the shape’s symmetry and the unchanging speeds/directions guarantee that a direction mismatch forces a meeting point.
Probability Computation for Three Ants
Thus, for three ants on a triangle, the probability that no collisions occur is 1/4.
Extending to k Ants on an Equilateral Polygon
For k ants on a k-sided regular polygon (equilateral polygon), the same logic holds. A collision-free scenario occurs only if all ants uniformly pick clockwise or all uniformly pick counterclockwise. Thus, the probability for no collision is:
Geometrical Insight
Visually, you can imagine each ant rotating about the polygon. If one single ant chooses a direction that is different from the others, it will inevitably meet the ant behind or in front of it at some vertex or partway along an edge. Only the scenario in which they all move as one continuous loop (fully clockwise or fully counterclockwise) preserves a constant separation among them.
Probabilistic Interpretation
Possible Follow-up Questions
How would the probability change if speeds differ?
What if ants are on a shape that is not regular?
How can we verify this probability numerically with a simulation?
One approach is to run a Monte Carlo simulation in Python. Below is an illustrative code snippet:
import random
def simulate_no_collision(num_ants, num_trials=10_000_00):
no_collision_count = 0
for _ in range(num_trials):
# Generate random choices of direction for each ant: +1 for clockwise, -1 for counterclockwise
directions = [random.choice([+1, -1]) for _ in range(num_ants)]
# Check if all directions are the same
if all(d == directions[0] for d in directions):
no_collision_count += 1
return no_collision_count / num_trials
k = 3
approx_probability = simulate_no_collision(k)
print(f"Approx probability for k={k} ants: {approx_probability:.5f}")
What if the ants can decide the direction at different times?
If the decision is still binary (clockwise or counterclockwise) but made at different instants, the essential logic does not change: collisions occur unless they end up collectively moving in the same direction at all points in time. If there is any moment in which at least one ant is going one way while another ant goes the opposite, eventually there will be an intersection along an edge or a vertex. The probability from the original statement assumes a single choice made simultaneously at the start. If directions can change over time, the problem changes dramatically because we need to consider dynamic rules for how they change direction.
Could collisions be prevented if ants can turn around mid-path?
Yes, in principle, if ants are allowed to change direction later, they could avoid collisions by timing their turns. But in the classic problem, ants keep the same chosen direction throughout their journey, which is why the analysis is straightforward. If mid-path turning were permitted, you would have a more complicated scenario requiring continuous-time or step-by-step analysis of each ant’s motion.
How does this relate to real-world random processes?
This puzzle is a good illustration of how small, distinct random choices can lead to inevitable interactions unless a rare combination aligns. In random processes (e.g., random walks, concurrency systems, or multi-agent simulations), the chance that multiple agents never “collide” is often tiny unless they all do exactly the same thing. This underscores the importance of independence assumptions in probability and how combinatorial outcomes (like matching vs. mismatching direction assignments) directly affect the system’s final behavior.
Below are additional follow-up questions
What if collisions are allowed to be “pass-throughs” where ants can move through each other without interacting?
In many real-world applications, objects or agents might effectively pass through one another (like photons in fiber optics or certain overlapping animations). If collisions no longer mean a forced “meeting,” the problem’s definition of “collision” changes. Formally, if ants can occupy the same point in space at the same time without colliding, then we’d need a revised definition of the event we want to avoid. In a practical sense, the probability of “no collision” in the classic sense becomes less relevant because collisions would not alter the ants’ paths. The key difference is that the notion of “never meet” now depends on whether the ants can share coordinates at the same time. If we allow them to ghost through each other without interacting, the probability that they “meet” might effectively become 1 for any differing directions, but it wouldn’t be a meaningful collision. Hence, for a pass-through interpretation, either every direction assignment is still possible, or we would redefine “meeting” so it means physically intersecting at a vertex or on an edge. Depending on how we interpret it, we might say collisions no longer matter, or we might say the probability of “never being at the same point at the same time” is as described. Overall, the biggest pitfall is ensuring clarity in whether a meeting is a genuine obstacle or just a coordinate overlap with no consequence.
How does the result change if ants can start from any point on the edges rather than just the vertices?
Would it matter if each ant chooses a direction with a probability other than 1/2 (e.g., 1/3 clockwise and 2/3 counterclockwise)?
Could the polygon be replaced by a circular track where each ant can choose a random starting point and direction?
What if each ant moves randomly at each step, flipping direction periodically rather than choosing once at the start?
When ants change direction over time, the problem transforms from a straightforward single-choice scenario into a Markov process or a random walk on a graph. Initially, we might think each ant decides “clockwise” or “counterclockwise” only once, but if that choice is repeated every time unit, the probability of eventual collision can be quite different. In fact, if directions can flip at any point, the probability that they never meet might drop to zero for an infinite time horizon, because eventually some random fluctuation might bring them together. A subtlety is that if they continuously and independently flip direction with a certain rate, collisions can happen arbitrarily many times, and only extremely particular histories in which the ants remain separated would avoid collisions. The main pitfall is conflating the single-choice result with ongoing, repeated random directions. One must move to a more advanced stochastic analysis in continuous or discrete time to fully characterize the probability of no collisions, and often that probability ends up being zero in the limit.
How might obstacles or changes in edge length affect the probability of collision?
Could we extend the problem to three dimensions, for example, ants on the vertices of a polyhedron?
Yes. Imagine ants on the corners of a 3D shape like a tetrahedron or cube, each choosing a route along the edges. The idea of “collision-free” travel can still hinge on whether they choose consistent paths that never intersect. However, in three dimensions, each vertex can have multiple edges emanating from it, and an ant might choose not just “clockwise or counterclockwise” but possibly multiple path options around the 3D structure. This greater number of path choices (and the geometry of 3D shapes) complicates the analysis. If we restrict the choice to two consistent loops around the shape—say a “clockwise loop” and a “counterclockwise loop,” carefully defining those loops on a 3D object—then you might still get a similar pattern: collisions are avoided if they all pick the same loop direction. However, verifying there are only two loops and ensuring the entire polyhedron’s edges form a consistent cycle is nontrivial. A common pitfall is assuming you can label edges “clockwise/counterclockwise” in the same way you do in a planar polygon; 3D shapes can allow many potential cycles, so the problem becomes a question of enumerating those cycles carefully.
How does the problem scale if we consider very large k, such as hundreds or thousands of ants and corners?
What if collisions cause ants to “bounce off” and reverse direction immediately upon contact?
Does the size of the polygon or the distance between corners affect the probability?
Under the classic interpretation where all edges of an equilateral polygon are the same length and each ant has uniform speed, the absolute dimensions (e.g., side length) do not matter for the probability of collision. The probability is governed by the binary direction choices alone. If you scale the polygon up or down, time to collision might change, but the probability of eventual collision stays the same. However, if each ant’s speed is not uniform across edges or if side lengths differ (thus losing the “equilateral” condition), that changes the nature of the collisions. A subtle pitfall is mixing up how distance scaling affects timing vs. probability. Probability in the classical sense is purely combinatorial (which set of directions do they choose?) rather than geometric measure in the continuum sense—distance rescaling does not affect the discrete choice probability.