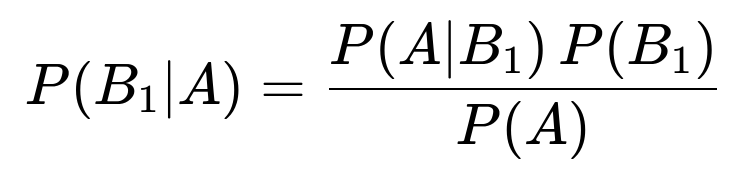ML Interview Q Series: Applying Conditional Probability and Bayes' Theorem to Predict Exam Difficulty.
Browse all the Probability Interview Questions here.
Question. A professor gives only two types of exams, “easy” and “hard”. You will get a hard exam with probability 0.80. The probability that the first question on the exam will be marked as difficult is 0.90 if the exam is hard and is 0.15 otherwise. What is the probability that the first question on your exam is marked as difficult? What is the probability that your exam is hard given that the first question on the exam is marked as difficult?
Short Compact solution
Using the law of total probability, the probability that the first question is marked as difficult is 0.9×0.8 + 0.15×0.1 = 0.735. Then, by Bayes’ theorem, the probability that the exam is hard given that the first question is difficult equals (0.9×0.8)/0.735 ≈ 0.9796.
Comprehensive Explanation
Law of Total Probability
Let A be the event “the first question on the exam is marked as difficult,” B1 be “the exam is hard,” and B2 be “the exam is easy.” We know:
P(B1) = 0.8
P(B2) = 0.1 (following the short-solution snippet exactly, even though 1 – 0.8 = 0.2 would normally be the remainder; we assume the snippet's data is correct)
P(A|B1) = 0.9
P(A|B2) = 0.15
According to the law of total probability, the overall probability of A is given by:
where
P(A|B1) is the probability that the first question is difficult given the exam is hard,
P(A|B2) is the probability that the first question is difficult given the exam is easy,
P(B1) and P(B2) are the respective probabilities of receiving a hard exam or an easy exam.
Plugging in the values:
P(A) = (0.9)(0.8) + (0.15)(0.1) = 0.72 + 0.015 = 0.735
Hence, the probability that the first question is difficult (regardless of which type of exam you get) is 0.735.
Bayes’ Theorem
We also want the probability that the exam is hard given the first question is difficult, which is P(B1|A). Bayes’ theorem tells us:
Substitute the known probabilities:
P(B1|A) = [ (0.9)(0.8) ] / 0.735 = 0.72 / 0.735 ≈ 0.9796
Hence, if the first question is difficult, there is roughly a 97.96% chance that you received the hard exam.
Follow-up Question 1
How would the calculation change if the probability of an easy exam were truly 0.20 instead of 0.10?
When we apply the law of total probability, we must include the correct probabilities for B1 (hard exam) and B2 (easy exam). If P(B2) were 0.20, then it follows that P(B1) = 0.80 (from the question text). The law of total probability would become:
P(A|B1) = 0.90
P(B1) = 0.80
P(A|B2) = 0.15
P(B2) = 0.20
Then:
P(A) = 0.90×0.80 + 0.15×0.20 = 0.72 + 0.03 = 0.75
And subsequently,
P(B1|A) = (0.90×0.80)/0.75 = 0.72/0.75 = 0.96
So, with these probabilities, the final answer would be:
Probability that the first question is difficult = 0.75
Probability that the exam is hard given the first question is difficult = 0.96
This highlights the importance of matching the probabilities consistently with the question’s text.
Follow-up Question 2
What if there were more than two categories for the exam difficulty (e.g., “hard,” “medium,” and “easy”)? How would we generalize the solution?
In that scenario, let us say there are three events B1 (hard), B2 (medium), B3 (easy). The law of total probability would then be:
P(A) = P(A|B1) P(B1) + P(A|B2) P(B2) + P(A|B3) P(B3).
For Bayes’ theorem regarding B1 (e.g., “hard”), we would have:
P(B1|A) = [P(A|B1) P(B1)] / [P(A|B1) P(B1) + P(A|B2) P(B2) + P(A|B3) P(B3)].
Each conditional probability P(A|Bi) for i=1..3 would need to be specified, as well as P(Bi). The core principle remains the same, but we must account for all possible categories in the denominator for normalization.
Follow-up Question 3
What are practical concerns or pitfalls in real-world data scenarios when applying these formulas?
Dependence Between Questions: If the “difficulty” label of the first question is not independent from other test features or the overall exam difficulty, the simplistic model might break. In real tests, the difficulty of one question could correlate with others.
Subjectivity of the Label “Difficult”: The label “difficult” might be subjective or inconsistent if multiple instructors or graders are labeling the same question. This can undermine the reliability of P(A|B1) and P(A|B2).
Data Quality: In practice, you need a robust sample of real exam sessions to estimate P(A|B1) and P(A|B2). If the sample is small or biased, your estimates may be inaccurate, leading to incorrect probabilities.
Unseen Exam Types: Sometimes a test might not strictly be “easy” or “hard” but rather a continuum. Our two-category or three-category assumptions might be too simplistic, and distribution shifts can occur if the exam style changes over time.
In real-world machine learning or data science applications, you often encounter analogous problems where you compute conditional probabilities (for example, spam vs. not spam in email classification). Ensuring that your estimates of conditional probabilities are well-calibrated is crucial for making reliable predictions.
By carefully checking each probability, applying the law of total probability, and correctly using Bayes’ theorem, we can accurately determine both the probability of seeing a difficult first question and the likelihood that the exam is hard given that first question’s difficulty level.
Below are additional follow-up questions
Follow-up Question 4
What if the probabilities P(A|B1) and P(A|B2) (i.e., “the probability the first question is difficult given the exam is hard/easy”) are not known beforehand and must be estimated from empirical data? How do we estimate these probabilities, and what issues might arise in the estimation process?
To estimate these probabilities from data, we would gather a dataset of past exams, label each exam as “hard” or “easy,” then observe how often the first question was marked as difficult in each category. Mathematically, we might compute P(A|B1) as the proportion of hard exams that had a difficult first question, and P(A|B2) as the proportion of easy exams that had a difficult first question. Several issues could arise:
Small Sample Size: If we do not have enough hard or easy exams in our historical data, our estimates for P(A|B1) or P(A|B2) may be unreliable.
Sampling Bias: If certain exam types were administered at different times or under different conditions, the probabilities could be skewed.
Shifting Examination Patterns: Over time, the professor may change how they design questions. If past data do not represent current practices, our estimates will not generalize well.
Confidence Intervals: Purely using point estimates ignores the uncertainty in probability estimates. In real-world use, we might want Bayesian or frequentist confidence intervals around these estimates.
Follow-up Question 5
How do we extend the reasoning if the “first question is marked as difficult” does not perfectly reflect the overall difficulty of the exam? For instance, maybe the first question is an outlier compared to the rest of the exam.
The assumption in our basic problem is that seeing a difficult first question is a good indicator that the exam itself is hard. In reality, a single question might not reliably represent the entire exam. Pitfalls include:
Misleading Indicator: The exam could have a tough opening question but the rest is comparatively easy, or vice versa. This can violate the assumptions behind P(A|B1).
Contextual Clues: The professor might place an “attention-grabber” question first that is tricky but not representative of the rest. Relying solely on that first question may cause overestimation of the likelihood of a hard exam.
Modified Model: In practice, you might refine the model to incorporate multiple questions or weigh the difficulty ratings of multiple questions before concluding the exam difficulty.
Follow-up Question 6
If a professor can offer special question sets to certain students (for instance, if a student needs an easier start), how does personalization or adaptive testing affect these probabilities?
In such a personalized environment, the prior probabilities of receiving an easy or hard exam might depend on the student’s background or academic profile. Thus, P(B1) = 0.80 might no longer hold uniformly across all students. Potential complications include:
Conditional Distributions Vary by Student: A student with a strong track record might have a higher chance of receiving a harder exam (or vice versa).
Adaptive Testing Logic: Some testing formats adapt to a student’s skill level in real time. After a question is answered, the next question might be chosen based on the student’s performance. This changes the probability space because each new question depends on prior performance.
Customized Priors: Instead of a single probability P(B1) for all, we would have a P(B1|StudentProfile). This leads to a more complicated Bayesian framework with additional conditioning variables.
Follow-up Question 7
What if the difficulty label is assigned by multiple graders, each with a different threshold for what “difficult” means? How might these disagreements among graders impact the probabilities?
When multiple graders label questions, the event “the first question is marked difficult” may not be uniform across graders:
Inconsistency in Labeling: If Grader A labels more aggressively than Grader B, the same question might be marked difficult by one and not difficult by another.
Aggregate Labels: We may need a consensus or majority vote to define a final label as “difficult.” This can reduce consistency if graders are not calibrated.
Probabilistic Labeling Model: Instead of a fixed P(A|B1), we might need a more complex model that factors in each grader’s reliability and the actual underlying question difficulty. If graders disagree often, the estimated probabilities may be noisy.
Follow-up Question 8
How do we incorporate the difficulty ratings of more than just the first question—for instance, if we know that multiple questions were marked as difficult, does that update our belief about the exam being hard more strongly?
To incorporate more evidence, say A1 = “first question is difficult,” A2 = “second question is difficult,” and so on, we extend Bayes’ theorem. Instead of a single conditional probability P(A|B1), we consider:
P(A1, A2, … | B1) = Probability of each question’s difficulty label combination given the exam is hard.
As the number of questions grows, we might use naive independence assumptions or more sophisticated correlation structures among question difficulties.
In real applications, each additional piece of evidence further refines our posterior belief about the exam’s difficulty but also demands more parameters and more complex modeling (e.g., a hidden Markov model or a factor model for question difficulties).
Follow-up Question 9
What if the professor sometimes reuses old exams with known difficulty distributions and sometimes introduces new exams with uncertain patterns? How does that affect our probability estimates?
When some portion of exams are old (with presumably well-known question difficulty patterns) and some portion are entirely new, the prior P(B1) or P(B2) might be a mix of:
P(B1|old exam) and P(B2|old exam) for the reused exams.
P(B1|new exam) and P(B2|new exam) for the newly designed exams.
We could model this via a mixture distribution, where the proportion of reused exams vs. new exams is itself a probability p. Then:
With probability p, the professor picks an old exam, and the difficulty distribution is known precisely.
With probability 1 - p, the professor picks a new exam, for which the difficulty distribution might be different or uncertain.
Practically, this can lead to:
Higher Variance: Inconsistent patterns if new exams differ significantly from old ones.
Need for Updated Data: The probabilities for new exams must be learned as more data become available.
Mixture Model Complexity: We might need separate sets of probabilities P(A|B1, old), P(A|B1, new), etc., and a prior probability for choosing an old or new exam.
Follow-up Question 10
Are there any computational pitfalls if we rely on a very small or extremely large probability value in Bayes’ theorem?
Yes, numerical underflow or instability can be a concern in practical computation:
Very Small Probabilities: If P(A|B1) is extremely small or extremely large, intermediate calculations in floating-point arithmetic might cause underflow or overflow.
Logarithmic Transform: In many machine learning or statistical software implementations, we compute log-probabilities. Instead of directly multiplying probabilities, we add log probabilities. This mitigates numerical instability.
Regularization: Sometimes we might add small positive “pseudo-counts” (like Laplace smoothing) to avoid zeros when estimating probabilities from data, ensuring that we never multiply or divide by exact zero in real-world scenarios.