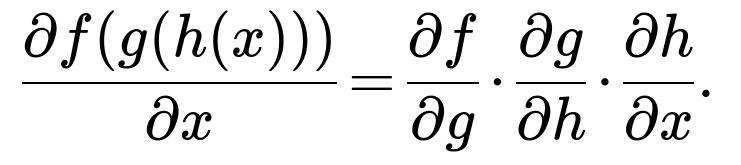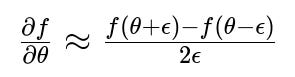ML Interview Q Series: Backpropagation Explained: Efficient Gradient Computation in Deep Networks via Chain Rule.

📚 Browse the full ML Interview series here.

Backpropagation (Chain Rule): Explain how backpropagation works in a neural network. Specifically, describe how the chain rule is used to propagate error gradients layer-by-layer from the output back to the inputs. Why is backpropagation critical for training multi-layer networks, and how does it handle updating millions of parameters efficiently?

Understanding backpropagation and the chain rule in a neural network

Backpropagation is an algorithmic procedure to compute the gradients of a loss function with respect to every parameter in a multi-layer neural network. It leverages the chain rule of calculus to achieve this efficiently. The entire goal is to measure how changing each parameter (weight and bias) will affect the final loss, and then use gradient-based optimization (e.g., stochastic gradient descent) to update those parameters and minimize the loss.

Forward pass

During the forward pass, data flows from the inputs to the outputs. At each layer, inputs are multiplied by weights, combined with biases, and then passed through an activation function. This propagates the signal deeper through the network until it produces an output. A typical layer operation can be expressed as:

Layer input→Multiply by weights→Add bias→Apply activation→Layer output.

After the final layer, we compute a loss function that captures how far the predicted output is from the target. The forward pass alone tells us how the network transforms inputs into outputs, but not how to adjust the network’s parameters to reduce the loss. This is where backpropagation enters.

Backward pass (applying the chain rule)

The chain rule of calculus states that if we have a composite function f(g(h(x))), then the derivative of the composite function with respect to x can be expressed as:

In a multi-layer neural network, our final loss L is a function composed of all the transformations from input to output. Each transformation typically involves a linear operation (weights, biases) followed by a nonlinear activation. When we apply the chain rule in the context of backpropagation, we systematically move layer by layer from the output (where the loss is computed) toward the input, multiplying the appropriate gradients at each step. This approach is highly efficient because each partial derivative is reused for earlier layers.

Critical nature of backpropagation for training multi-layer networks

Neural networks can contain dozens, sometimes hundreds of layers. Backpropagation allows the gradient to be computed in a way that reuses calculations and avoids computing partial derivatives from scratch for every parameter. By breaking the entire transformation into smaller, layered functions, the chain rule supplies a way to distribute the loss gradient back through each layer. Without backpropagation (or some variant of it), finding gradients for millions of parameters in a deep network would be computationally infeasible.

Updating millions of parameters efficiently

In practice, modern frameworks like PyTorch or TensorFlow construct a computational graph where every operation is tracked. When you call the backward pass, these frameworks automatically apply the chain rule to compute gradients with respect to every parameter. They then update all parameters in a single pass via vectorized operations. This vectorization is crucial for speed. For example, matrix-vector multiplications are heavily optimized in low-level libraries (e.g., BLAS, cuBLAS on GPUs), and the backpropagated gradients can also be expressed in vectorized form. This parallelization lets a single backward pass handle millions (or even billions) of parameters.

Implementation details in Python (PyTorch example)

Below is a concise code snippet in Python using PyTorch to demonstrate how the forward and backward passes work. Even though PyTorch automates backpropagation, conceptually it’s executing the chain rule on your computational graph behind the scenes:

import torch
import torch.nn as nn
import torch.optim as optim

# Simple neural network with one hidden layer
class SimpleNet(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(SimpleNet, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        x = self.fc1(x)
        x = self.relu(x)
        x = self.fc2(x)
        return x

# Define a small example
input_size = 10
hidden_size = 20
output_size = 1

model = SimpleNet(input_size, hidden_size, output_size)
criterion = nn.MSELoss()       # Just an example loss
optimizer = optim.SGD(model.parameters(), lr=0.01)

# Dummy input and target
x = torch.randn(5, input_size)  # Batch of 5 samples
target = torch.randn(5, output_size)

# Forward pass
output = model(x)
loss = criterion(output, target)

# Backward pass (PyTorch automatically applies backprop via the chain rule)
optimizer.zero_grad()
loss.backward()

# Update parameters (all updates done in one vectorized operation)
optimizer.step()

In this code, the call to loss.backward() triggers PyTorch to traverse the computational graph from the final output (the loss) back through the layers to compute gradients for each parameter. This computation is extremely fast because it is vectorized and makes heavy use of efficient linear algebra operations under the hood.

Subtleties and practical considerations

Using the chain rule in deep networks can lead to issues like exploding or vanishing gradients. Proper weight initialization, careful activation function choices (e.g., ReLU variants), and normalization techniques (batch norm, layer norm) help mitigate these. Optimizers like Adam, RMSProp, or momentum-based SGD can also help stabilize and speed up training.

How does the chain rule expand in a multi-layer scenario?

What is the difference between the forward pass and backward pass in computational terms?

During the forward pass, you:

• Take input data and multiply/add with parameters.

• Pass results through activation functions.

• Propagate these computations layer by layer until you compute a final output and a loss.

During the backward pass, you:

• Start from the loss function at the output.

• Apply the chain rule to systematically compute partial derivatives of the loss with respect to each layer’s outputs, then each layer’s parameters.

• Move from the final layer back to the first layer, accumulating gradients along the way.

One key computational difference is that the forward pass typically involves direct matrix multiplications and activations, whereas the backward pass involves these same or transposed matrix operations combined with derivative computations for each activation. Frameworks store intermediate results (activations, etc.) from the forward pass to make gradient computation efficient.

Why do vanishing and exploding gradients occur, and how can we mitigate them?

Vanishing gradients happen when repeated multiplication of small derivative terms through many layers causes gradients to shrink, hindering weight updates in early layers. Exploding gradients happen when derivatives become very large. Techniques to mitigate these issues include:

• Using activation functions such as ReLU or variants instead of sigmoid/tanh for deep layers.

• Employing careful weight initialization schemes (He initialization, Xavier/Glorot initialization).

• Applying normalization (batch normalization, layer normalization).

• Clipping gradients if they exceed a threshold to prevent excessively large updates.

• Using sophisticated optimizers like Adam or RMSProp that adaptively adjust the learning rate.

Why do we typically initialize weights randomly, and how do frameworks implement partial derivatives?

If all weights were initialized identically, each neuron would perform exactly the same computation, leading to no ability to learn distinct features. Random initialization helps break symmetry among neurons. Frameworks that implement automatic differentiation (e.g., PyTorch, TensorFlow) build a computational graph where every operation (matmul, activation) keeps references to the values needed for gradient computation. When you call the backward routine:

• The framework traverses this graph in reverse (backprop).

• Applies the chain rule at each node to compute the relevant partial derivatives.

It uses these derivatives to update the parameters. This entire procedure is typically implemented in efficient C/C++ backends with parallelism on GPU/TPU hardware.

How do we handle millions or billions of parameters efficiently in practice?

Modern systems exploit the following:

• Vectorized operations: Instead of computing each weight’s gradient individually, the framework computes gradients for entire tensors in parallel.

• GPU acceleration: GPUs are well-suited to large-scale linear algebra operations needed for backprop.

• Memory management: Intermediate activations for the forward pass are usually stored temporarily for backward pass calculations, and frameworks sometimes use checkpointing or gradient checkpointing to balance memory usage and computational cost.

• Distributed training: We can use multiple GPUs or even multiple machines to handle very large models, splitting the computation of forward and backward passes across devices.

How does backpropagation extend to complex architectures like RNNs or Transformers?

In recurrent neural networks (RNNs), backpropagation is extended through time (Backpropagation Through Time, BPTT). This unrolls the RNN across time steps and applies the chain rule through those unrolled steps.

In Transformers, the main operations are multi-head attention and feed-forward blocks, but it is still the same idea: the computational graph tracks each operation, and the chain rule is applied in reverse to compute derivatives. While the details of the architecture differ, the underlying principle—applying the chain rule for gradient calculation—remains the same.

Are second-order derivatives (e.g., Hessians) used in practice for training deep networks?

In classical optimization, one might use second-order methods like Newton’s method that rely on the Hessian (matrix of second derivatives). For large neural networks with millions or billions of parameters, constructing and inverting such a Hessian matrix is computationally prohibitive. In practice, we rely on first-order methods like SGD, momentum, Adam, etc. Some advanced techniques approximate second-order information (e.g., quasi-Newton methods, K-FAC for natural gradient), but pure second-order methods remain uncommon for large-scale neural networks due to computational cost.

Why might backpropagation fail if the network is not properly set up?

If the network has no appropriate activation function or if the activation saturates in certain regions, gradients may either vanish or blow up. If the learning rate is too high, the network might not converge. If the data is not properly scaled or normalized, the network may learn very slowly or diverge. Proper architecture, initialization, normalization layers, and hyperparameters are essential for reliable backpropagation.

How does autodiff handle branching structures (e.g., skip connections, branching layers) in modern networks like ResNet?

Frameworks handle this by representing the network as a directed acyclic graph (DAG). Each operation that splits the signal or merges it (e.g., skip connections) becomes a node with multiple inputs/outputs. When it’s time to backprop, the framework sums gradients flowing from all the branches that feed into a node. This general graph-based approach ensures that any structure—whether a skip connection or more intricate branching—can be differentiated without special handling.

What are the main steps to tune or debug backpropagation if the model doesn’t train?

Common troubleshooting steps include:

• Checking that the loss decreases over time: If it stays constant or diverges, confirm the data is correct, the network is properly connected, and the learning rate is appropriate.

• Looking at gradient norms: If they are zero or extremely large, suspect a vanishing/exploding gradient problem.

• Monitoring weight updates: If weights aren’t changing, verify gradients are being computed and the optimizer is actually being called.

• Trying simpler models or smaller networks to see if they can learn a basic pattern. If they can’t, there may be a data or implementation bug.

How can we interpret gradient-based learning in a high-level sense?

Each parameter’s gradient indicates the instantaneous rate of change of the loss with respect to that parameter. Negative gradients lead to parameter updates that, if repeated over many training steps, collectively move the model toward configurations with better performance on the given data. By iterating this procedure across many batches of data, the model statistically converges to a region of parameter space that minimizes the loss.

---

Below are additional follow-up questions

How do we incorporate explicit constraints or regularization into the backpropagation pipeline?

In many real-world applications, we may want certain constraints on the parameters of a model (for example, weights that sum to 1 or non-negative weights) or forms of regularization that explicitly penalize certain parameter configurations (such as or group sparsity). When we talk about backpropagation, we typically think of just the main loss term, but in constrained or regularized optimization, an additional penalty or constraint term is added to the loss function.

If you need constraints like non-negativity, one approach is to parameterize the weights in a way that enforces non-negativity by definition. For instance, you could parameterize w=exp⁡(θ), which is always positive. The parameter θ in that exponential form is unconstrained, and thus can be freely updated via standard backprop. The backprop framework will then produce gradients for θ, and w itself will remain positive.

If you impose a penalty, such as an penalty (weight decay), it is generally straightforward because it just adds a term proportional to the sum of squared weights in the loss. During backprop, that penalty’s partial derivatives will appear as a term λ⋅w in the gradient (where λ is the regularization factor). penalty leads to a subgradient operation λ⋅sign(w), which is easy to incorporate in modern frameworks. However, can cause weights to become exactly zero (which is beneficial for sparsity) but can be trickier to optimize with plain gradient-based methods; specialized optimizers or proximal methods might be used in some cases.

Pitfalls: • If the regularization term is large or if constraints are too strict, the network might underfit. • can lead to discontinuities at zero, so frameworks often implement subgradient methods to handle that. • Hard constraints (like weights that sum to 1) can require custom parameterization or post-processing of gradients to project onto the feasible set, which can be computationally costly for large models.

Edge cases: • Very large regularization coefficients can make the training procedure converge to trivial solutions (e.g., all weights near zero). • In some architectures that share parameters, applying constraints or regularizers consistently across shared parameter blocks requires careful coding and verification.

How does backpropagation handle piecewise-defined or non-smooth activation functions like ReLU or hard-sigmoid?

ReLU (Rectified Linear Unit) is defined as ReLU(x)=max⁡(0,x). Although it’s piecewise linear, it has a kink at x=0. Its derivative is 1 for x>0 and 0 for x<0, which is still well-defined almost everywhere except exactly at x=0. The set of points where x=0 has measure zero in a continuous distribution of inputs, so in practice this doesn’t cause major issues for gradient-based optimization. Frameworks implement the derivative as 1 for x>0, 0 for x<0, and often 0 or 1 for x=0 by convention.

For other piecewise-defined or non-smooth activations (hard-sigmoid, leaky ReLU with different slopes), the same principle applies: the piecewise derivative is used wherever it is defined. The chain rule can still be applied as long as the function is differentiable almost everywhere. In a non-smooth region, an appropriate subgradient or convention is usually chosen.

Pitfalls: • If a large portion of neurons are on the zero side of ReLU, gradients can become sparse and hamper learning (the so-called “dying ReLU” phenomenon). • Hard-sigmoid, or any other function with plateau regions, can lead to vanishing gradients in those plateaus if inputs get stuck there.

Edge cases: • If the input distribution shifts during training, many neurons might saturate (all outputs either 0 or large positive values) and you can lose gradient signal. • In certain hardware or library implementations, boundary points can behave inconsistently if not carefully handled.

What are the differences between forward-mode and reverse-mode automatic differentiation, and why is reverse-mode typically used in deep learning?

Forward-mode automatic differentiation computes derivatives by propagating differential quantities from the inputs forward to the outputs. Reverse-mode (backpropagation) does the opposite: it starts from the output and propagates derivatives backward to the inputs.

In a deep neural network, typically the function has far fewer outputs (often just a scalar loss) than inputs (all the parameters). Reverse-mode AD is more efficient because it allows computing gradients with respect to all parameters in roughly the same complexity as a single forward pass (plus a similar cost for the backward pass). If we used forward-mode for a network with millions of parameters, we would need to run it potentially millions of times to get each parameter’s derivative individually.

Pitfalls: • If your problem had far fewer inputs than outputs, forward-mode might be more convenient. But this is not the common scenario in deep learning. • Implementing forward-mode for large neural nets can be done, but it is typically more memory-intensive or more time-consuming when you have many parameters.

Edge cases: • In certain specialized tasks (like computing Jacobian-vector products for some advanced meta-learning or second-order method), forward-mode AD might be used. But for standard deep networks, reverse-mode is almost always used.

What is gradient checking, and how do we verify correctness of a backpropagation implementation?

Gradient checking is a method to ensure the analytic gradients computed by backprop match numerical approximations of those gradients. One typical numerical approximation is:

where f(θ) is the loss function, and θ is a particular parameter. If the analytic gradient is correct, it should be extremely close to the finite-difference estimate for sufficiently small ϵ.

Pitfalls: • Floating-point arithmetic errors can occur if ϵ is too small. If ϵ is too large, the approximation might become inaccurate. You may need to experiment with different ϵ values. • This check can be very slow for large models because you need to evaluate f(θ+ϵ) and f(θ−ϵ) for each parameter or a subset of parameters. • Some advanced layers or operations might require special handling if they involve random sampling or non-deterministic behaviors.

Edge cases: • If a layer includes non-differentiable operations or random sampling, gradient checking will need to fix the random seed or remove the randomness to be consistent with the finite-difference approximation. • If regularization or constraints are included, ensuring those terms are included in the check is necessary to get a full picture of correctness.

How is backprop applied to architectures that have gating mechanisms or multi-branch flows, such as in attention layers or advanced RNN cells?

Modern neural architectures often contain gating, attention, or multi-path branches (e.g., gating in LSTM cells, attention in Transformers, multi-headed branches). Each of these components can be seen as just another differentiable building block. The frameworks create a graph that branches out at these gates and merges back in subsequent layers. During the backward pass, the automatic differentiation engine sums or splits gradients appropriately based on how the data flows forward. In attention, you typically compute attention scores, reweight them, and combine them with the input representations. Backprop flows through these operations by differentiating the attention mechanism with respect to the scores and the underlying transformations.

Pitfalls: • If the gating function saturates or the attention scores become extremely skewed (e.g., near 1 for one position and near 0 for all others), gradient flow might be weak for certain branches. • Incorrectly broadcasting or reshaping tensors can break the computational graph or lead to dimension mismatches that cause silent errors or NaNs in gradients.

Edge cases: • In multi-branch networks, if one branch is not used frequently (for example, if a gate is nearly always closed), that branch may receive almost no gradient signal, effectively never learning. • Weight sharing across branches or inside gating mechanisms can lead to complex gradient flows that might overshadow or diminish learning in certain sub-networks if not balanced or normalized.

How do we deal with layers or operations that are not differentiable, such as rounding or discrete sampling?

Some neural network operations are inherently non-differentiable (like discrete sampling of a random variable) or have zero gradient almost everywhere (like the rounding function). Standard backprop cannot pass gradients through these operations in the usual way. Solutions include:

• Straight-through estimators: In some reinforcement learning or quantized network contexts, you might implement a “straight-through” gradient that simply pretends the derivative is 1 (or some constant) during backprop, even though the forward pass uses a rounding or discrete step. • REINFORCE or policy gradient methods: If the operation corresponds to sampling from a distribution, you can use gradient estimators from RL or approximate the gradient via methods like the reparameterization trick (for continuous distributions) or Gumbel-Softmax (for discrete distributions). • Surrogate gradients: For certain approximate operations, a differentiable surrogate function is used for backprop while the forward pass still uses a piecewise constant or discrete function.

Pitfalls: • Straight-through estimators can be unstable or inaccurate, leading to biases in gradient estimates. • The variance in REINFORCE-based gradient estimates can be extremely high, slowing convergence.

Edge cases: • If your model mixes differentiable and non-differentiable components in a large architecture, you must carefully track which parts can pass gradients normally and which require specialized estimators, or you might end up with zero or undefined gradients. • Some hardware or software frameworks might not fully support these specialized gradient estimators out of the box.

How does backprop interact with meta-learning or hyperparameter optimization?

In meta-learning, the idea is to learn how to learn, often involving a nested optimization procedure (an outer loop that updates meta-parameters and an inner loop that updates model parameters). Backprop can extend to second-order derivatives if you need to differentiate through the learning process itself. For instance, in MAML (Model-Agnostic Meta-Learning), you do a forward pass and backward pass for the inner update, then differentiate again through that update in an outer loop.

For hyperparameter optimization, certain methods attempt to backprop not just through the model parameters but also through hyperparameters (like learning rates or layer coefficients) by including them in the computational graph. This requires you to treat hyperparameters as differentiable parameters.

Pitfalls: • In meta-learning, naive second-order gradient computations can be computationally expensive if your model is large. Approximations or gradient checkpointing might be needed to reduce memory usage. • If the hyperparameter is not differentiable in how it affects the training loop, standard backprop can’t be used (e.g., a discrete hyperparameter like batch size).

Edge cases: • Large models with large outer-loop steps can lead to high memory usage, requiring truncated or approximate backprop. • Overfitting the meta-parameters to a particular training set distribution can happen if the meta-learning or hyperparameter optimization is not carefully regularized.

How is backprop used when weights are shared across different parts of the network, as in Siamese networks or shared embeddings?

When weights are shared, we have multiple forward passes through the same parameter set. The computational graph in frameworks will treat these shared weights as pointers to the exact same parameters. The forward pass uses them in different branches or time steps, but there’s only one set of parameters. During backprop, gradients from each usage of those weights are summed together so that all references to the shared weights are updated consistently.

Pitfalls: • If you accidentally duplicate parameters instead of referencing the same ones, you won’t get the benefits of weight sharing. This can lead to mismatch between the intended design and the actual model. • The gradient signals might conflict if the different branches have contradictory objectives. The net result could be suboptimal or require a carefully tuned loss weighting.

Edge cases: • When partial sharing is used, making sure only some parameters are shared while others remain distinct can be tricky to implement. • If each branch has drastically different data distributions, the single shared weight set might not be optimal for either distribution.

What issues might arise when implementing custom layers, and how can we debug them in backprop?

In many real-world projects, you might implement custom layers or operations in frameworks like PyTorch or TensorFlow. You typically provide a forward function (calculations from inputs to outputs) and rely on the framework’s automatic differentiation. However, if you do something unusual, you may need to manually define the backward pass.

Issues might include: • Incorrect shapes or broadcasting: A mismatch in tensor shapes or dimension ordering can lead to silent errors or runtime shape errors. • Not retaining intermediate variables: If you accidentally overwrite or free a buffer that’s needed for gradient calculation, you could get NaN gradients or an error about missing gradient data. • In-place operations that break the computational graph: Some frameworks disallow or restrict in-place modifications of tensors that require gradient tracking.

Debugging strategies: • Use small test inputs and manually compare partial derivatives with finite differences (gradient checking). • Print or log intermediate tensors and their gradients to see if they become NaN or explode. • Use built-in debugging tools or hooks in the framework (e.g., PyTorch hooks) to examine the forward and backward passes.

Edge cases: • If your custom layer has conditionals or loops, the control flow can be tricky for the automatic differentiation engine. • If the custom operation depends on external state not captured in the computational graph, you might not get correct gradient flows.

How do we handle the batch dimension during backprop, especially when computing partial derivatives for multiple samples simultaneously?

In deep learning, we typically process a batch of samples at once to leverage parallel hardware. The forward pass for a batch is a vectorized operation on all samples, and the backward pass aggregates gradients across the batch. Formally, the loss is often defined as the average over the batch. The gradient with respect to a parameter is then the average over that parameter’s gradient contribution from each sample in the batch.

Implementation details: • The framework will automatically sum (or average) the gradients over the batch dimension. • You can control how the final loss is aggregated (for example, using “mean” versus “sum” in PyTorch’s nn.MSELoss). This choice affects the scale of the gradients.

Pitfalls: • If your batch size is very small or changes frequently (like in variable batch size training), you may see fluctuating gradient magnitudes. • Large batch sizes can lead to stable gradient estimates but might require adjusting the learning rate.

Edge cases: • When performing custom computations, if you forget to reduce the loss properly over the batch dimension, you could inadvertently blow up your gradient or incorrectly scale it. • Some tasks (like certain ranking or metric learning tasks) compute a complex multi-sample loss that couples samples within a batch, which can complicate the gradient calculation.

How do we manage the memory footprint in backprop for large-scale networks, and what is gradient checkpointing?

In big models, storing all intermediate activations for the backward pass can be huge. This can easily exceed GPU memory, especially when dealing with very deep networks or large batch sizes. Gradient checkpointing is a technique to trade off compute for memory. Rather than storing every intermediate activation, the method selectively stores only certain checkpoints. During the backward pass, the missing intermediate activations are recomputed from the nearest checkpoint, allowing a significant reduction in memory usage at the cost of extra forward computation.

Pitfalls: • Increased computation time because of repeated forward passes. • Need to carefully place checkpoints to balance memory savings and compute overhead.

Edge cases: • For extremely large models, even checkpointing might not be enough, requiring model parallelism or specialized hardware. • In recurrent architectures, gradient checkpointing can significantly reduce memory usage for long sequences, but also slow down training because it requires multiple partial forward passes.

What is gradient accumulation, and how does it help when you have constraints on batch size or memory?

Gradient accumulation is a technique where you split your batch into smaller micro-batches that fit in memory. You run a forward and backward pass on each micro-batch, adding (accumulating) the gradients to a running total without updating the parameters. After processing all micro-batches in that larger batch, you perform one optimizer step. This effectively simulates a larger batch size than what you can fit in GPU memory at once.

Practical considerations: • You must ensure that you do not zero out gradients until you have completed all micro-batches that form the effective batch. • You typically scale the learning rate or the gradients to account for the effective batch size.

Pitfalls: • If you forget to reset or scale gradients correctly, your parameter updates can become incorrect. • The training speed might drop because you’re doing multiple forward/backward passes for what conceptually is a single batch update.

Edge cases: • If your dataset or approach relies on strictly random sampling across a large batch for stable gradient estimates, micro-batch-based gradient accumulation might have slightly different statistical properties. • Real-time or online learning scenarios often can’t use large-scale accumulation if data must be processed sequentially without storing many samples.