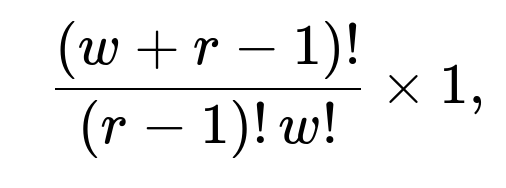ML Interview Q Series: Ball Color Depletion Probability Solved Using Last Ball Symmetry
Browse all the Probability Interview Questions here.
A bag contains r red balls and w white balls. We draw balls one by one without replacement until all remaining balls in the bag are of the same color. Determine the probability that the white balls are depleted first.
Short Compact solution
One way to view this is to consider the color of the very last ball in a random ordering of all the balls. Since any ball is equally likely to appear in the final position, the probability that the last ball is red is r/(r+w). If the last ball is red, then all the white balls must have been drawn out first. Therefore, the probability that white balls are exhausted before the red balls is r/(r+w).
Another combinatorial justification counts how many ways we can choose an arrangement of draws that ends with the red ball and thus removes all whites first. That also leads to the same ratio r/(r+w) when summed over all possible orders of drawing.
Comprehensive Explanation
The Core Idea of “Last Ball” Argument
A particularly intuitive way to solve this problem is to reason that all (r+w) balls can be placed in a random sequence. Because all permutations are equally likely when you draw without replacement, the probability of any specific ball (or color) being in the last position is determined only by how many such balls exist. In other words, out of r+w total balls, r are red, so the probability the last ball is red is
If the final ball in that entire sequence is red, then by the time you reach that last ball, you will have removed all w white balls. Hence, the probability of exhausting white balls first is precisely the same as the probability that the final ball is red, which gives r/(r+w).
Combinatorial Perspective
An alternative, more “counting-based” approach is to count the number of ways to arrange the draws so that the w white balls all appear before the last red ball is drawn:
We know the process stops once there is only one color left in the bag. For white balls to be removed first, all w white balls must occur in the sequence of draws before the $r$th red ball appears.
One can carefully count the number of permutations in which w white balls appear among the first (r+w−1) draws, with the final (i.e., $(r + w)$th) draw forced to be red. Then compare that count against the total number of permutations of r+w distinct balls.
Although this counting can be written in factorial terms, it collapses neatly to the same fraction r/(r+w). Hence both the counting viewpoint and the “last-ball” viewpoint line up perfectly.
Edge Cases and Additional Remarks
If r=0 (all white balls), then obviously the probability that white balls are exhausted first is 0 (since they’re already the only color).
If w=0 (all red balls), then the probability is 1 that “white balls are exhausted first,” though this scenario is degenerate because there are no white balls at all.
If r or w is very large compared to the other, the fraction r/(r+w) or w/(r+w) might become quite small or large, consistent with the intuition that the color with the larger count is less likely to get used up first.
This type of reasoning (looking at the final position of a random permutation) often appears in other contexts—such as finding the probability that a certain color (or object) is the last to appear.
Potential Follow-up Question 1
Why does considering the color of only the last ball validly determine the probability that we run out of white balls first?
Because drawing balls without replacement essentially creates a random permutation of all r+w balls. Whichever color ball ends up at the end of that permutation can never be fully removed until that last position is reached. If a red ball is last in the arrangement, that means all w white balls must have been drawn before you get to that final red ball, implying white is depleted first. By symmetry, each ball is equally likely to occupy that final position, so the probability of seeing a red ball last is r/(r+w).
Potential Follow-up Question 2
Can we formalize the combinatorial argument with factorials?
Yes. Consider the number of ways to order w+r distinct balls. There are (r+w)! possible permutations. Now, suppose we want all w white balls to appear among the first (r+w−1) positions (so that the last ball is red). The last position is fixed as red, so we only permute the remaining (w+r−1) positions among w white and (r−1) red. The count of such permutations is
because we choose which of the (w+r−1) slots go to the ww whites, and the remaining (r−1) must be red. Then we multiply by the ways to order those whites among themselves and reds among themselves if the balls were thought of as distinct. Either way, after dividing by the total permutations (r+w)!, one arrives at the same ratio r/(r+w).
Potential Follow-up Question 3
What happens if the drawing is not purely random or not equally likely for each ball at each draw?
The fundamental assumption in this problem is that each draw is uniformly random among the remaining balls. If that is altered (for example, if certain balls have a higher chance of being drawn at each step), then the analysis would need to account for those biases. In that case, the intuitive last-ball argument breaks down because the distribution of which ball ends up last is no longer uniform. You would then need to set up a different probability model or rely on Markov chain arguments, depending on the nature of the sampling bias.
Potential Follow-up Question 4
How could we verify this probability via a quick simulation in Python?
A simulation would straightforwardly confirm the analytical result by randomly drawing balls many times and recording the fraction of trials in which the white balls get depleted first. For instance:
import random
def simulate_draws(r, w, num_simulations=10_000_00):
count_white_out_first = 0
for _ in range(num_simulations):
# Create a bag with 'r' red ('R') and 'w' white ('W') markers
bag = ['R']*r + ['W']*w
random.shuffle(bag)
# We draw until all remaining are same color
red_count = r
white_count = w
for ball in bag:
if ball == 'R':
red_count -= 1
else:
white_count -= 1
# Stop if only one color remains
if red_count == 0 or white_count == 0:
# Check if white balls were depleted first
if white_count == 0 and red_count > 0:
count_white_out_first += 1
break
return count_white_out_first / num_simulations
# Example usage
r, w = 3, 5
estimated_prob = simulate_draws(r, w)
theoretical_prob = r/(r + w)
print(f"Estimated Probability: {estimated_prob}")
print(f"Theoretical Probability: {theoretical_prob}")
The fraction estimated_prob should converge to r/(r + w) if the number of simulations is large enough. This numerical experiment aligns with both the last-ball reasoning and the combinatorial approach.
Potential Follow-up Question 5
Could you elaborate on real-world analogies or scenarios where a similar principle applies?
A classic related problem is the “inspection paradox” in reliability theory or certain gambler’s ruin problems where sequences of events occur, and one is interested in which type of event occurs last. Another example is in random permutations of a deck of cards: if we label certain cards of interest (e.g., suits) and wonder about the chance that a particular suit appears last, the principle is analogous. The essential takeaway is that if all outcomes are equally likely, focusing on which item ends up at the final position in a random permutation is a simpler and more elegant route to the solution.
Below are additional follow-up questions
What if the bag contained more than two colors? How would that affect the probability of depleting a specific color first?
Symmetry Approach (Heuristic) Each color can be viewed as equally likely to finish last in a random permutation if the counts are the same. However, if the counts differ, it alters the probabilities. A known result for the probability that a particular color is the first to run out is roughly proportional to that color’s initial count, under certain symmetrical assumptions. But the exact formula can be more involved.
Pitfalls and Edge Cases
Unequal counts: If a color has a very small number of balls compared to others, it is more likely to run out first.
Large k: As the number of colors increases, direct enumeration or simple combinatorial expressions become unwieldy.
Real-world complexities: In real scenarios with multiple categories (like different product SKUs in an inventory), a single, simple ratio-based formula might not suffice. One might need simulation or more advanced combinatorial derivations.
Ultimately, the extension to multiple colors requires careful combinatorial reasoning or a simulation-based approach to glean the probability that any one color gets depleted first.
How can partial replacement or replenishing of balls change the probabilities of running out of a color?
When you allow for partial replacement or replenishment, the dynamic changes significantly:
Replacement After Each Draw If each ball drawn is returned to the bag with some probability or a new ball is added, the sequence of draws does not create a simple random permutation of a fixed set of balls. Instead, you have a Markov chain where the state space is defined by how many red and white balls remain at each step. This can shift probabilities because every draw influences the subsequent composition of the bag in a non-trivial way.
Intermittent Replenishment In some practical problems, you might restock the bag after certain intervals. This can decrease the likelihood that any color is fully exhausted at all, or at least postpone it. The probability of depleting a given color might drop drastically if frequent replenishment events occur.
Pitfalls and Edge Cases
Infinite supply: If a color can be replenished without limit, then that color may never be “exhausted,” and the concept of running out is moot.
Non-uniform replenishment: If one color is replenished more often than another, that color is less likely to be the first to go.
Real-world scenario: Inventory management systems often restock products in bursts. The mathematics of depletion requires a discrete-time or continuous-time Markov chain approach.
Hence, once any form of replenishment is introduced, the elegant r/(r+w) style argument no longer applies, and one must rely on a more elaborate probabilistic or simulation-based model.
What if each ball had a different probability of being drawn, rather than uniform?
If some balls are more likely to be drawn than others (for instance, weighted by size, shape, or any other property), the uniform-random-permutation assumption breaks:
Weighted Draws In this scenario, at each draw, you are more likely to pick certain colors if they collectively have a higher total “weight.” Even if one color has fewer balls, if each of its balls is weighted heavily, it might still get drawn at a higher frequency. This can change which color empties first.
Markov Model with State Transition Instead of uniform sampling, you must define transition probabilities. The chance of drawing a ball of a certain color depends on the sum of the weights of all balls of that color divided by the total weight of all remaining balls in the bag. Then, one can model how many balls remain for each color as you proceed. The solution might involve setting up a system of difference equations or employing a Markov chain approach.
Pitfalls and Edge Cases
Very large or small weights: If one color’s weight is extremely high relative to others, it will almost certainly be drawn more often, speeding its depletion.
Continuous vs. discrete: Some weighting systems may approximate continuous distributions of “selection probability,” raising further complexity.
Real-world parallels: Weighted sampling arises when, for instance, items have different probabilities of being defective or singled out for inspection.
You lose the simple “look at the last ball” logic because not all permutations are equally likely. Instead, each distinct order has its own probability based on the product of weights at each draw.
What if we analyze the number of draws needed until the first color is depleted, rather than just which color depletes first?
Another interesting twist is to ask about the distribution or expected value of the number of draws required until one color is gone:
Expected Number of Draws One might ask, “On average, how many draws does it take to remove all the white balls (if white is indeed the color that empties first)?” This is a different question because the problem originally focuses on probabilities of color exhaustion, not the timing.
Detailed Breakdown To find the expected number of draws for the event “some color is fully removed,” you often sum over all possible ways this can occur. Alternatively, you may use negative hypergeometric distributions, which precisely deal with the distribution of draws needed to observe all of one type.
Pitfalls and Edge Cases
Ties: There can be a scenario where red and white become 1 and 1 near the end, and you must track who gets picked next.
Multiple Colors: If more than two colors are present, computing the expected time to the first depletion can become complex.
Real-world scenario: In a production scenario, this might relate to how quickly a material is used up in an assembly line, with consequences for reordering timelines.
The negative hypergeometric distribution is often used to handle “draws until the last success” or “draws until a certain category is exhausted,” which is mathematically more involved than the simpler ratio-based question.
How would this probability or reasoning change if we stopped drawing as soon as exactly one ball of a specific color remains?
In some applications, you might stop not when an entire color is depleted but when you’re down to a certain threshold. For instance, you could stop drawing when you have exactly one white ball left:
Modified Stopping Rule The event “Stop when exactly one white ball remains” is a different condition from “Stop when no white balls remain.” In that case, you’re no longer looking for a color to be entirely exhausted but rather a partial state of the system. This modifies the problem’s boundary condition.
Probability Shifts
If you stop as soon as color i hits a predefined threshold (like one ball), the last-ball argument no longer applies. You must count sequences in which color i hits that threshold first, while the other colors still have at least that threshold.
The probability can be computed through hypergeometric or Markov chain approaches that track how many of each color remain at every step.
Pitfalls and Edge Cases
Threshold Zero vs. Non-zero: If the threshold is zero (the original problem), we have the simpler ratio. If the threshold is positive, each color might need multiple steps to reach that threshold, making the counting complicated.
Real-world analogy: In an inventory system, you might restock at a reorder point (e.g., exactly one item left on the shelf). The question is then, “Which product hits that reorder point first?” That has a different distribution from actually running out completely.
What if we require that the same number of red and white balls remain for us to stop drawing?
A different but related line of questioning is: “We draw until there are x red and x white left in the bag. What is the probability that x is reached for the first time with white exactly at x simultaneously with red exactly at x?” Although not the same question, it touches on interesting stopping-time conditions.
Equal Count Stopping Condition Under this condition, we only stop when the bag has the same number of white and red balls. The probability distribution of the draws leading to that moment is typically tackled using combinatorial methods or reflection principles (a concept in random walks).
Connection to Random Walks If we think of red draws as +1 steps and white draws as -1 (or vice versa), then having an equal number of red and white balls left is akin to returning to a certain level in a one-dimensional walk, but with absorbing boundaries when we fully use up a color. This is more complicated because the ratio-based approach no longer applies directly.
Pitfalls and Edge Cases
If x=0: Then it is the original question (the point at which we have 0 left of either color).
Small bag sizes: With few balls, combinatorial enumerations might be feasible, but for large r and w, advanced or approximate methods are needed.
Real-world scenario: Imagine trying to maintain a balanced supply of two raw materials that need to be present in equal amounts for production. Understanding the probability that you reach a balanced state might matter for scheduling.
This question is somewhat tangential to the original problem but highlights how variations in the stopping rule can drastically change the analysis.
How would we handle a scenario where the drawing sequence can be paused or where the color of the next draw can be chosen?
In certain real-world setups, we might have the option to “choose” which ball to draw next or skip a draw, so the selection is no longer random:
Strategic Draws If you can decide to draw from a certain subset of the bag, or if you have any control over the draw, the problem becomes one of game theory or optimization. You might ask, “What strategy ensures I deplete color white first with high probability?”
Adaptive Stopping Perhaps you can pause drawing once you see that a certain color is low in number, hoping to keep that color from being removed. This changes the probability model significantly.
Pitfalls and Edge Cases
Partial Observability: If you don’t know how many red or white remain but have partial signals, your strategy might be imperfect.
Constraints: If the real environment forces random draws anyway, you can’t implement a strategy, so the original approach applies.
Complex strategy space: With large r and w, enumerating strategies is not trivial.
This scenario underscores that the original ratio-based approach critically depends on purely random draws with no external control or bias.
What if the outcome of interest is the color that remains at the end, rather than which is removed first?
Another angle is: “We keep drawing until one color is gone, and we want to know which color is left.” This is simply the complement event. If the white balls are exhausted first, it means the red color is the one that remains. Conversely, if red is exhausted first, then white remains. Thus:
Direct Complement The probability that red remains at the end is the probability that white is exhausted first, which we have as r/(r+w). So the probability that white remains at the end (meaning red is exhausted first) is w/(r+w).
Pitfalls
Edge Cases: If r or w is 0 initially, the outcome is determined outright.
Multiple Colors: With more colors, “the color that remains at the end” is a more complicated event, as multiple colors might remain if the first to run out is not unique.
Still, in the two-color scenario, it is a straightforward complement relationship.
How do errors or misclassification of color during drawing change the analysis?
In a real-world context, sometimes an item might be misclassified—imagine a scenario with uncertain detection of color due to poor lighting or sensor error:
Misclassification Probability If each ball draw has a probability p of being incorrectly identified as the other color, then you don’t reliably know if you truly removed a white or a red each time. Over many draws, the tallies you keep of each color can become inaccurate.
Practical Implications
You might incorrectly believe you have removed a white ball when you actually removed a red ball, causing an erroneous count. Eventually, you might think white is depleted, even though it’s not.
Or you might keep drawing because you think red remains, when in fact it was depleted earlier due to multiple misclassifications.
Modeling Such Errors You could incorporate misclassification rates into a Bayesian update process. The probability that color white is actually depleted would be conditioned on the observed draws and the known error rates. This typically requires a more advanced probabilistic framework or a simulation approach.
Edge Cases
Low error rates: Might have a minor effect but could still matter in borderline scenarios.
High error rates: The notion of depleting a color becomes very fuzzy because your entire tracking is unreliable.
These questions demonstrate that small changes to assumptions—like introducing human or sensor error—can necessitate a far more complex modeling approach.