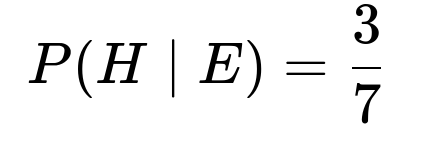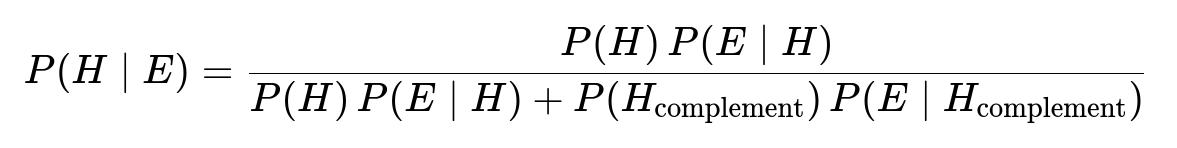ML Interview Q Series: Bayes' Odds Form: Solving Conditional Probability for Family Gender Composition
Browse all the Probability Interview Questions here.
A family is chosen at random from all three-child families. What is the probability that the chosen family has one boy and two girls if the family has a boy among the three children? Use Bayes’ rule in odds form to answer this question.
Short Compact solution
From the sample space of all three-child families, define event H as “the family has one boy and two girls” and its complement H_complement as “the family does not have exactly one boy and two girls.” We have:
P(H) = 3/8
P(H_complement) = 5/8
P(E|H) = 1 (E is “at least one boy”)
P(E|H_complement) = 4/5
Using Bayes’ rule in odds form:
P(H|E) / P(H_complement|E) = (P(H) / P(H_complement)) × (P(E|H) / P(E|H_complement)) = (3/8 ÷ 5/8) × (1 ÷ 4/5) = (3/5) × (5/4) = 3/4
Hence P(H|E) = (3/4) / (1 + 3/4) = (3/4) / (7/4) = 3/7.
Comprehensive Explanation
Bayes’ theorem is often expressed in several forms, one of which is the odds form. In this problem, we define:
H = “The family has exactly 1 boy and 2 girls.”
H_complement = “The family does not have exactly 1 boy and 2 girls.” Equivalently, it has either 0, 2, or 3 boys.
E = “There is at least one boy in the family.”
We want P(H|E), which is “The probability that the family has 1 boy and 2 girls, given that it has at least one boy.”
First, consider how P(H) = 3/8 is found. There are 2^3 = 8 equally likely ways to assign boy/girl to three children, assuming a 1/2 probability for each child being a boy or a girl, independently. The event H (1 boy, 2 girls) can happen in three distinct ways (BGG, GBG, GGB), so P(H) = 3/8. Its complement H_complement thus has probability 5/8.
Next, we compute P(E|H) and P(E|H_complement):
If H occurs (exactly 1 boy, 2 girls), then we definitely have at least one boy. So P(E|H) = 1.
If H_complement occurs, that event includes outcomes with 0, 2, or 3 boys. Among those, only the case of 0 boys fails E. Specifically, of the 5 ways in H_complement (BBB, GGG, BGB, GBB, BBG, ... though enumerating carefully we see the total is 5 from the full 8 minus 3 ways of H), four of them have at least one boy (everything but GGG). Hence P(E|H_complement) = 4/5.
We now use the odds form of Bayes’ theorem:
We plug in the numbers:
The prior odds ratio P(H)/P(H_complement) is (3/8) ÷ (5/8) = 3/5.
The likelihood ratio P(E|H)/P(E|H_complement) is 1 ÷ (4/5) = 5/4.
Multiplying these gives 3/5 × 5/4 = 3/4. This is the posterior odds of H versus H_complement given E. Converting odds to probability, we note:
P(H|E) = (3/4) / (1 + 3/4) = (3/4) / (7/4) = 3/7.
Hence,
This illustrates a common probability puzzle: given at least one boy, the probability that the family has exactly one boy (and hence two girls) is 3/7.
One potential confusion is that if the condition had been “the oldest child is a boy” instead of “at least one boy,” the probability changes. But here, the condition is that there is at least one boy among the three children, which leads us to 3/7.
In general, Bayes’ rule in odds form is a handy variant of Bayes’ theorem:
It helps to avoid some fraction manipulations and can make certain probability updates more straightforward.
Possible Follow-up Questions
Could we solve this using the direct formula for conditional probability instead of odds form?
Yes. The standard form of Bayes’ theorem is:
Plugging in:
P(H) = 3/8
P(E|H) = 1
P(H_complement) = 5/8
P(E|H_complement) = 4/5
We get:
P(H|E) = [ (3/8) × 1 ] / [ (3/8) × 1 + (5/8) × (4/5 ) ] = (3/8) / [ (3/8) + (4/8 ) ] = (3/8) / (7/8) = 3/7.
How can we simulate this in Python to empirically verify the result?
We can write a quick simulation:
import random
def simulate(num_trials=10_000_000):
count_condition = 0
count_event = 0
for _ in range(num_trials):
children = [random.choice(['B','G']) for _ in range(3)]
if 'B' in children: # at least one boy
count_condition += 1
if children.count('B') == 1:
count_event += 1
return count_event / count_condition
print(simulate())
If we run a large number of trials, the result should approach 3/7 ≈ 0.42857.
Why is the probability not 1/3 if we argue “one boy, two girls is one scenario, two boys, one girl is another scenario, three boys is another scenario” among those with at least one boy?
This is a common misunderstanding. The event E = “at least one boy” has multiple ways to occur. Of those ways, some sets of outcomes are more numerous in the sample space than others. Specifically, “three boys” is just one arrangement (BBB), whereas “one boy, two girls” can appear in three distinct orders (BGG, GBG, GGB), and “two boys, one girl” also can appear in three distinct orders (BBG, BGB, GBB). Counting each arrangement as equally likely reveals the probability is 3/7 for exactly one boy among those families that have at least one boy.
What if the interview question changes to “the first child is a boy” or “at least one boy born on a Tuesday”?
Changing how we condition on “having a boy” can significantly alter the set of possible outcomes. For instance:
If the condition is “the first child is a boy,” that’s a different event that excludes half of the sample space (any family whose first child is a girl is removed). So the conditional probability changes accordingly.
The famous “boy born on a Tuesday” puzzle is a more subtle example: if we condition on the fact that there is at least one boy who was born on a Tuesday, the sample space and counting logic become more intricate. This changes the final probability compared to the simpler “at least one boy” condition.
These variations emphasize how carefully specifying the condition can greatly change the probability result.
Below are additional follow-up questions
What if the probability of having a boy is not exactly 1/2 for each birth?
If real-world data suggests that the probability of a newborn being male is slightly different from 0.5 (for instance, approximately 0.51 in some countries), this changes the underlying distribution of all possible three-child families. In that case, the probabilities P(H) and P(H_complement) are no longer 3/8 and 5/8. Instead, if p is the probability of a child being male, then for exactly one boy out of three children, we must compute 3 * p * (1 - p)^2. For zero boys, it would be (1 - p)^3, and so forth. The event E = “at least one boy” similarly has a different probability: 1 - (1 - p)^3.
To incorporate this into Bayes’ theorem, one would substitute these expressions for P(H), P(H_complement), P(E|H), and P(E|H_complement). P(E|H) might remain 1 if H is exactly one boy and two girls, but the rest would shift, and we’d need to re-derive the final value for P(H|E). This scenario underscores how Bayes’ rule depends on the accuracy of one’s prior assumptions about distribution parameters.
What if families do not stop at three children if they haven’t had a boy?
Some families may continue having children until they have at least one boy (or at least one girl). This “stopping rule” complicates the assumption that we have a simple uniform distribution of births. If an interviewer modifies the question by introducing these real-world behaviors, the sample space of “three-child families” is no longer straightforward. Some families might reach three children only after they got a boy or might not appear in this population if, for example, they had a boy earlier and decided to stop at fewer children.
In a scenario involving such stopping rules, we must carefully define how families of exactly three children came to exist (did they choose to stop at three regardless of gender, or did they stop because they reached some threshold?). Once that process is understood and modeled, the prior P(H) changes dramatically. The event “at least one boy” might be very likely if families who had no boy by child two decided to keep trying, thus potentially affecting the distribution of families with exactly three kids.
How do correlated outcomes across children affect the result?
A classical assumption is that each birth is independent with probability 1/2 for a boy or girl. However, there could be factors that correlate sibling sexes, such as certain genetic or environmental influences. If births are not truly independent, enumerating the probabilities in a simple 2^3 manner might be incorrect. For example, if there is a small correlation that once a firstborn is male, subsequent siblings are slightly more likely to be male, that alters the distribution of (B, B, B) vs. (B, G, G) and so on.
In an interview, one must clarify whether the question assumes independent births with a 50–50 chance. If an interviewer pushes on real-world data or correlated events, the Bayes’ approach still applies, but you must recalculate each probability using the correct joint distribution. This is a subtle point: Bayes’ rule itself remains valid, but the specific numeric results rest on the correct modeling of the underlying probabilities.
Could prior information about the children's ages change the analysis?
Sometimes, interview questions add details like, “We learn that the oldest child is at least 10 years old,” or “We know the middle child is a teenager,” etc. Including ages affects the prior because it can exclude certain families who might not have an older child or re-weight how likely it is for a family with certain ages to also have certain genders. If the event E is “at least one boy,” combined with knowledge about ages, we must re-express the sample space of “three-child families” that meet this demographic. The probabilities P(H), P(E|H), and so on might shift if age distribution correlates with the probability of each gender.
In an extreme example, if we are told the oldest child is 17, it might reflect generational or cultural differences in birth rates over time, so we would no longer treat each child’s gender as a simple 1/2 chance for each birth. Real-world data might show changing birth ratios over multiple years. If an interviewer poses such scenarios, it tests whether the candidate can adapt Bayesian reasoning to more complex prior information.
What if the question is asked in the context of multiple families drawn from real data?
An interviewer might ask, “How would you handle this problem if you have a dataset of 1 million families with exactly three children? How would you empirically estimate the probability that a randomly chosen one has exactly one boy and two girls, given that at least one child is a boy?” The direct approach is to filter all three-child families from the dataset, then further filter those with at least one boy, and measure the fraction that have exactly one boy. You get an empirical approximation P(H|E). This fosters a practical discussion about using data-driven methods (frequentist approaches) vs. theoretical Bayesian priors. It also raises questions of data quality: how reliable is the dataset, does it have sampling bias, and are all families in the population equally represented?
What happens if “family” is defined differently, e.g., including foster children or stepchildren?
In some real-world cases, you might not have a simple scenario where three consecutive births come from the same parents. A family may have stepchildren, foster children, or adopted children, and the probability distribution of their genders might differ from the classical “three births from a single mother” assumption. If the question modifies “three-child family” to “a household with three children under 18, regardless of how they joined the family,” you again shift the probability model. The set of ways that three children of various genders enter a household is different from three biological births. This can be a subtle test to see if the candidate recognizes that the underlying generative assumptions for births are no longer straightforward.
How do we approach the scenario if we misinterpret the event E?
A classic pitfall is to assume E is “the oldest child is a boy” or “the first child we happen to observe is a boy” when the question states “at least one boy” among three children. Misreading or misapplying the condition can lead to the incorrect 1/3 or 1/2 results instead of 3/7.
An interviewer could ask how we ensure we are applying the correct condition. The key is to carefully distinguish between:
E = “at least one boy in the family” (meaning any child).
E = “the oldest child is a boy.”
E = “we see a boy playing outside, but do not know which child this is.”
E = “at least one boy in the family was born in a particular month or on a particular day.”
Each of these statements conditions the sample space in different ways. Not clarifying precisely which child is being discussed or how the child is identified leads to confusion. In practical Bayesian analysis, one must precisely define E so as not to overcount or undercount certain outcomes.
Would the approach change if we replaced “boy” and “girl” with two other categories?
Yes, though the arithmetic is the same if we simply rename the events to something else with equal probabilities. However, if we replace “boy” vs. “girl” with “child has some trait vs. does not have that trait,” it generalizes the logic of the problem to any scenario where each individual in a group can independently possess or lack a certain characteristic. The structure of Bayes’ rule doesn’t change; what shifts is the interpretation of each probability. This is sometimes done in genetics or in marketing contexts, where “boy” might be replaced by “in the target demographic,” “girl” replaced by “not in the target demographic,” and so on. If the probabilities differ for each category, or if occurrences aren’t independent, all those details must be factored in similarly to the boy-girl problem.
If an interviewer asks about these re-labeled events, it tests whether you can abstract away from the typical boy-girl puzzle and apply the same Bayesian reasoning in more general contexts without confusion.