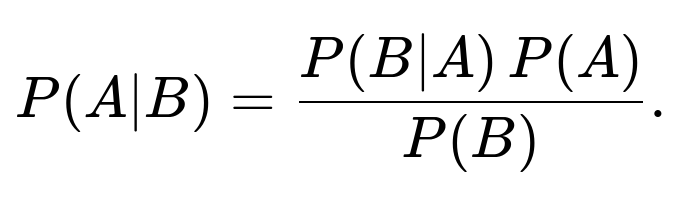ML Interview Q Series: Bayes' Theorem for Interpreting Positive Diagnostic Tests with Low Disease Prevalence.
Browse all the Probability Interview Questions here.
In a population, exactly 1 out of every 1000 individuals carries a particular disease. There is a diagnostic test that will correctly detect the disease in 98% of those who have it, and it also has a 1% false positive rate for those who do not have the disease. If a person’s test result comes back positive, what is the probability that this individual actually has the disease?
Short Compact solution
Let the event that a person has the disease be A, and let the event that the test result is positive be B. We want to find P(A∣B). By Bayes’ theorem:
which is about 8.93%.
Comprehensive Explanation
Bayes’ theorem is used to compute the probability that an event occurs given that some evidence (test outcome) is observed. In this context:
A is the event that an individual has the disease. B is the event that the individual’s test result is positive.
We know the following:
The prevalence of the disease is 0.1% (or 1 out of 1000), so P(A)=0.001. If an individual does have the disease, the probability of testing positive is 98%, so P(B∣A)=0.98. This is often called the sensitivity or true positive rate. If an individual does not have the disease, the probability of testing positive (false positive rate) is 1%, so P(B∣A′)=0.01.Equivalently, if someone is healthy, 99% of the time they get a negative result, and 1% of the time they falsely test positive. Since most people do not have the disease, this 1% false positive chance significantly impacts how likely a person is to be truly infected if they receive a positive test result.
Using Bayes’ theorem, the probability that someone truly has the disease given a positive test is:
The trickiest part is P(B), the probability of testing positive overall. This can happen if the individual truly has the disease and tests positive or if the individual does not have the disease yet still tests positive. That is:
or about 8.93%. This means that, despite a test that seems accurate at first glance, fewer than 1 in 10 individuals who get a positive result truly have the disease, due to the low prevalence and the influence of false positives from the much larger healthy population.
Why This Makes Sense
Even though the test has a high sensitivity of 98%, there are so many more healthy people (999 out of 1000) that a 1% false positive rate contributes enough positive results among healthy people to overshadow the positive results from the relatively tiny group of infected people. This phenomenon is often referred to as the “false positive paradox,” emphasizing the importance of the base rate or prior probability of a condition when interpreting diagnostic tests.
Follow-up question: How would changing the disease prevalence affect the probability?
If the disease prevalence P(A) increases, the fraction of truly positive individuals in the population also rises. With all else held constant (same sensitivity and false positive rate), the probability P(A∣B) would increase because the numerator in Bayes’ theorem would grow, while the denominator would not grow as significantly in comparison. Conversely, if the prevalence decreases even further (e.g., 1 in 10,000), the probability P(A∣B) would be even lower than 8.93%.
Follow-up question: What if we repeated the test?
If an individual tests positive once, and then takes a second, independent test, we can update our estimate by using the newly computed posterior probability as the prior in a new round of Bayes’ theorem. Conceptually, if the second test is also positive, that strengthens the evidence that the person is truly infected, thereby raising P(A∣B) after the second test. If the second test is negative, it reduces that probability drastically. This approach is commonly used in medical practice, where a second test or confirmatory test is often performed after an initial positive result.
Follow-up question: How do we implement a basic simulation in Python?
It can be helpful to run a quick simulation to see the empirical probabilities align with the theoretical Bayes calculation. One might write code like this:
import random
def simulate_test(n=1_000_000, p_disease=0.001, sensitivity=0.98, false_positive_rate=0.01):
# Counters
diseased_and_positive = 0
total_positive = 0
for _ in range(n):
# Determine if individual has the disease
has_disease = (random.random() < p_disease)
if has_disease:
# Probability of testing positive if diseased
test_positive = (random.random() < sensitivity)
else:
# Probability of testing positive if healthy
test_positive = (random.random() < false_positive_rate)
if test_positive:
total_positive += 1
if has_disease:
diseased_and_positive += 1
# Estimated probability that a person has the disease given a positive test
return diseased_and_positive / total_positive if total_positive > 0 else 0.0
prob_estimate = simulate_test()
print(prob_estimate)
In large simulations, you should see an empirical result that hovers near 0.089, which is about 8.9%, matching the Bayesian calculation.
Follow-up question: What if the test accuracy is reported differently for false negatives?
In many real-world scenarios, tests might have separate false negative and false positive rates instead of just a single “accuracy” figure. If the test fails to detect the disease in 2% of diseased individuals (which corresponds to a 98% sensitivity), that remains consistent with our assumption. However, if false negatives are more frequent or less frequent, or if we had a separate specificity metric (the probability of testing negative when healthy), the calculations would adjust accordingly. The main principle remains the same: Bayes’ theorem always requires the prior probability of the condition, the sensitivity, and the specificity (or false positive rate) to compute the posterior probability accurately.
Below are additional follow-up questions
What if the test performance varies across different demographic groups?
Real-world medical tests often perform differently across sub-populations (for instance, due to genetics, comorbidities, or access to healthcare). Suppose one demographic group experiences a higher false positive rate or a lower sensitivity than another. In that case, the calculation for P(A∣B) changes based on that subgroup’s unique P(B∣A) and P(B∣A′). A single “average” false positive rate might mislead policy decisions or diagnostic conclusions if large differences exist among subgroups.
Potential Pitfall: Ignoring heterogeneous false positive and false negative rates can produce incorrect estimates for certain populations. For instance, if a group has a false positive rate of 5% (instead of 1%), people from that group who test positive would have a lower P(A∣B) compared to the overall average.
Edge Case: Tests calibrated mainly on one demographic could show degraded performance in another demographic, resulting in over- or under-diagnosis. This phenomenon underscores the importance of stratifying data and analyzing test performance across all relevant sub-populations.
How do we adjust our calculations if the test results are not strictly binary?
In practice, many diagnostic tests yield a continuous measurement (e.g., antibody concentration, or a numeric index), and a threshold is chosen to classify the result as positive or negative. Depending on how we select that threshold, sensitivity and specificity change.
Potential Pitfall: If we adjust the cutoff to reduce false positives, we risk increasing false negatives (and vice versa). This trade-off is often depicted by the Receiver Operating Characteristic (ROC) curve.
Edge Case: An “indeterminate” range may exist, meaning the test result is borderline. In such cases, a second test or a more definitive confirmatory method is usually employed to refine the probability. Modeling these borderline results can be more complex but generally still relies on Bayesian ideas, where each test outcome (high, medium, low) updates the prior in a more nuanced way than a simple positive/negative approach.
What if test results are correlated over time or across individuals?
In many real-world scenarios, test outcomes are not strictly independent. For instance, consider a healthcare setting where a lab device might consistently overestimate biomarkers in certain samples, or a familial grouping where having multiple infected individuals might influence the probability another relative is infected.
Potential Pitfall: Traditional Bayes’ theorem formulations typically assume independence. If results have correlations—for example, the same lab error or contamination repeating across samples—the combined evidence from multiple positive tests might not be as strong as one would assume with full independence.
Edge Case: In epidemiological contexts, if family members or close contacts tend to share risk factors, a positive test in one household member raises the prior probability for another member, altering P(A) in a contact-tracing scenario. Failing to account for such dependencies can lead to overestimating or underestimating the true disease probability.
What if there is a cost or risk associated with false positives?
Medical tests do not exist in a vacuum. Each additional confirmatory test might be invasive, expensive, or stressful. While Bayes’ theorem gives the probability of disease, real-world decision-making must weigh the consequences of a false positive (e.g., unnecessary invasive procedures) versus a false negative (missing a real disease).
Potential Pitfall: Without considering practical costs (monetary, health, psychological), relying solely on P(A∣B) might lead to suboptimal healthcare decisions. For diseases where a false negative is very dangerous (e.g., highly lethal infections), some clinicians prefer a lower threshold for suspecting disease. Conversely, for less severe ailments or where confirmatory testing is risky, minimizing false positives might take priority.
Edge Case: If the confirmatory test is extremely expensive or harmful, you might be forced to rely on the single test result. In such a situation, even a high false positive rate might be prohibitive if the disease prevalence is low, because you would end up subjecting too many healthy individuals to unnecessary procedures.
How do we handle imperfect estimates of sensitivity and specificity?
In reality, estimates of test sensitivity and specificity come from clinical trials or observational studies, each with confidence intervals. If our test’s sensitivity is “around 98%” but could range from 95% to 99%, our posterior probability range might vary substantially.
Potential Pitfall: Using fixed point estimates (e.g., “1% false positive rate”) could lead to unwarranted precision in P(A∣B). Real-world data might show that the test is only 97% accurate in certain settings, or 99% in others, changing the Bayesian calculation non-trivially.
Edge Case: When the confidence intervals of sensitivity and specificity are wide, it might be beneficial to report a credible interval for P(A∣B). If a test might have anywhere from 1% to 2% false positive rate, the posterior probability for the disease given a positive result could vary from about 8% to perhaps well above 15%. This uncertainty affects clinical decisions and screening policy design.
How do prior beliefs or other clinical indicators factor in?
The simple calculation of P(A∣B) uses a single prior—P(A) based on population prevalence. However, in many medical contexts, doctors also have other clinical indicators such as symptoms, travel history, family medical history, or prior test results. All these can refine the prior probability before the test is even performed.
Potential Pitfall: Relying purely on population-level prevalence could ignore critical personalized factors. For example, if someone has a high-risk lifestyle or a cluster of symptoms consistent with the disease, the effective prior probability for that individual is higher than 0.1%. Conversely, someone with no risk factors at all might have an even lower prior.
Edge Case: In certain rare conditions, family history might multiply the prior probability drastically, making the test result interpretation far different from the population-level assumption. If these factors aren’t explicitly included in the Bayesian update, the estimate of P(A∣B) can be misleading.
What if the test is used repeatedly in mass screening over time?
When a large-scale screening program recurs (e.g., annual checkups or daily rapid tests for an infectious disease), individuals who test negative once might come back for repeated testing, and the prevalence might shift over time as new infections appear or old cases resolve.
Potential Pitfall: The independence assumption is challenged once you keep testing the same cohort repeatedly. After repeated negative results, a person’s probability of having the disease might go down, but not necessarily to zero. Also, the chance of disease introduction or reintroduction over time can change the base rate.
Edge Case: In dynamic settings, you might need a probabilistic model that updates each individual’s prior based on test history, exposure risk, and time intervals. For instance, in a pandemic, the prevalence can spike quickly, so the base rate from last month becomes out of date, requiring real-time Bayesian updates.
How does this analysis change if we have multiple mutually exclusive diseases?
If the same symptoms or the same biomarker can result from one of several diseases, the probability of having a specific disease given a positive result might need to be broken down among multiple competing conditions. Each disease would have its own prevalence and test characteristics.
Potential Pitfall: Simply applying Bayes’ theorem for a single disease can be incomplete if the positive test might also indicate a different disease with similar markers.
Edge Case: If a second disease is much more common and produces the same test outcome, you might have a situation where most of the “positive” results are actually from that second disease. In this scenario, we need a more general Bayesian framework that partitions the sample space among all diseases and updates each disease probability accordingly.