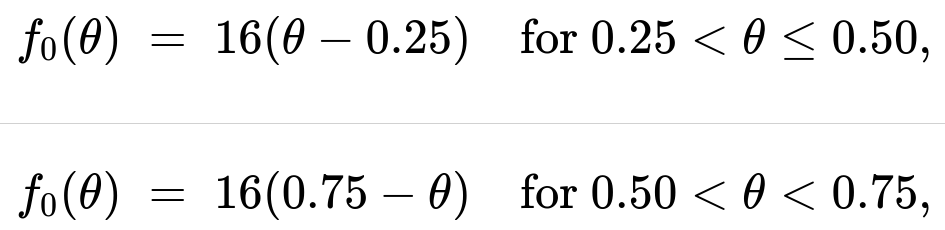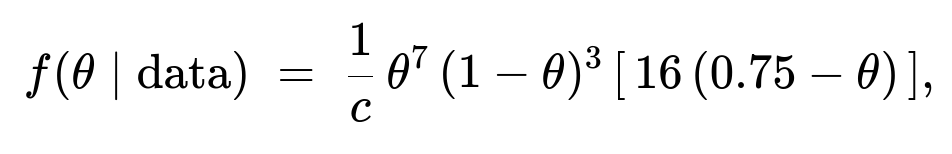ML Interview Q Series: Bayesian Estimation of Free Throw Success Probability with a Triangular Prior.
Browse all the Probability Interview Questions here.
Your friend is a basketball player. To find out how good he is at free throws, you ask him to shoot 10 throws. Your prior density f₀(θ) of the success probability θ of these free throws is a triangular density on (0.25, 0.75) with mode at 0.50. Specifically,
and f₀(θ) = 0 otherwise. Given your friend scores 7 times out of the 10 throws, find:
The posterior density function f(θ) of the success probability given the data.
The value of θ that maximizes this posterior density (the posterior mode).
A 95% Bayesian confidence interval for θ.
Short Compact solution
The likelihood based on 7 successes out of 10 is proportional to θ⁷(1−θ)³. Therefore, the posterior density is proportional to the product of the prior and the likelihood. Since the prior is triangular on (0.25, 0.75), the resulting posterior is piecewise:
For 0.25 < θ < 0.50:
For 0.50 < θ < 0.75:
and f(θ | data) = 0 outside (0.25, 0.75). The normalizing constant c ensures the total area under the posterior is 1.
Numerical calculations show that the posterior mode is θ ≈ 0.5663. Solving the integral of f(θ | data) from 0.25 to x = 0.025 and from x to 0.75 = 0.975 yields the 95% Bayesian credible interval (0.3883, 0.7113).
Comprehensive Explanation
Posterior Derivation
We denote θ as the probability that your friend makes a free throw. After observing the data (7 successes out of 10 attempts), the posterior distribution for θ is proportional to the prior distribution multiplied by the likelihood.
The likelihood from 7 successes and 3 misses is θ⁷ (1−θ)³.
The prior f₀(θ) is triangular on (0.25, 0.75), peaking at 0.50.
Hence,
posterior ∝ ( prior ) × ( likelihood ) which implies
f(θ | data) ∝ θ⁷ (1−θ)³ f₀(θ).
Because f₀(θ) = 0 outside (0.25, 0.75), the posterior is also 0 outside that interval. Inside (0.25, 0.75), f₀(θ) is piecewise:
For 0.25 < θ ≤ 0.50, f₀(θ) = 16(θ−0.25).
For 0.50 < θ < 0.75, f₀(θ) = 16(0.75−θ).
Thus we write:
0.25 < θ < 0.50:
0.50 < θ < 0.75:
and f(θ|data) = 0 otherwise.
Here, c is the normalizing constant ensuring that the entire posterior integrates to 1. In other words, c is computed so that
∫ f(θ|data) dθ = 1
over θ in (0.25, 0.75).
Finding the Posterior Mode
The posterior mode is the θ that maximizes f(θ|data). Within each interval (0.25 < θ < 0.50) and (0.50 < θ < 0.75), one can compute the derivative of the unnormalized posterior expression with respect to θ and set it to zero. Numerically, one finds the mode to be approximately 0.5663.
95% Bayesian Credible Interval
To find the 95% credible interval, we solve for the lower and upper bounds ℓ and u such that
∫ from θ=0.25 to θ=ℓ of f(θ|data) dθ = 0.025 and ∫ from θ=0.25 to θ=u of f(θ|data) dθ = 0.975.
Numerical integration shows ℓ ≈ 0.3883 and u ≈ 0.7113.
Hence, the 95% Bayesian credible interval for θ is (0.3883, 0.7113).
Potential Follow-Up Question: Why is the Posterior Piecewise?
Because the prior itself is piecewise-defined—one linear segment for (0.25, 0.50) and another for (0.50, 0.75)—the posterior inherits this piecewise nature. Multiplying θ⁷(1−θ)³ by a linear function of θ in each sub-interval naturally yields separate functional forms. However, the transition at θ=0.50 is smooth because both pieces match up to create a continuous posterior at that boundary. The only difference is the slope changes at θ=0.50.
Potential Follow-Up Question: How Does This Differ From a Flat Beta Prior?
If we had used a standard Beta(1,1) “flat” prior on (0,1), the posterior would simply have been Beta(8,4). However, here the triangular prior focuses probability mass in (0.25, 0.75) and peaks at 0.50, so it shifts the posterior distribution accordingly. This is one of the benefits of Bayesian methods: we can incorporate domain knowledge (e.g., we assume your friend’s free-throw percentage is almost certainly between 25% and 75%) directly into the analysis.
Potential Follow-Up Question: Could We Use MCMC Here?
In principle, yes. Even though the posterior here can be integrated (or approximated numerically) in closed form, for more complex models you might resort to Markov Chain Monte Carlo (MCMC) to sample from the posterior distribution. You would set up a Metropolis–Hastings or Hamiltonian Monte Carlo sampler, define the prior and likelihood, and generate posterior samples. However, for a 1D problem, direct numeric integration or grid approximation is typically simpler and faster.
Potential Follow-Up Question: How Does the Posterior Behave Near the Boundaries?
Since the prior is 0 outside (0.25, 0.75) and remains positive inside this interval, the posterior automatically becomes 0 outside. Near θ=0.25 or θ=0.75, the prior term (θ−0.25) or (0.75−θ) approaches 0, so the posterior density also goes to 0 at the boundaries of that interval, assuming the likelihood does not blow up (which it does not in this scenario).
Potential Follow-Up Question: Implementation Details in Python
You could implement a numeric approximation of the posterior in Python by evaluating the unnormalized posterior on a grid of θ values between 0.25 and 0.75, normalizing by the sum (or trapezoidal integral), and then calculating the cumulative distribution to extract credible intervals. Here is a simple illustration:
import numpy as np
# Define posterior function (unnormalized) using piecewise prior
def unnormalized_posterior(theta):
if theta < 0.25 or theta > 0.75:
return 0.0
like = (theta**7) * ((1 - theta)**3)
if theta <= 0.50:
prior = 16 * (theta - 0.25)
else:
prior = 16 * (0.75 - theta)
return like * prior
# Create a grid
theta_vals = np.linspace(0.25, 0.75, 10000)
post_vals = np.array([unnormalized_posterior(t) for t in theta_vals])
norm_const = np.trapz(post_vals, theta_vals)
posterior_vals = post_vals / norm_const
# Posterior mode (approx)
mode_index = np.argmax(posterior_vals)
posterior_mode = theta_vals[mode_index]
# Cumulative distribution for credible intervals
cdf_vals = np.cumsum(posterior_vals) / np.sum(posterior_vals)
# 2.5th percentile
lower_bound = theta_vals[np.searchsorted(cdf_vals, 0.025)]
# 97.5th percentile
upper_bound = theta_vals[np.searchsorted(cdf_vals, 0.975)]
print("Posterior mode:", posterior_mode)
print("95% Credible interval:", (lower_bound, upper_bound))
Running this approximate approach numerically will give estimates close to the analytic answers: a posterior mode near 0.5663 and a 95% credible interval around (0.3883, 0.7113).
Below are additional follow-up questions
What if the data violate the i.i.d. assumption (e.g., your friend’s performance changes from shot to shot)?
In Bayesian inference, a core assumption often used is that each shot is an independent Bernoulli trial with a fixed probability θ. However, in practice, your friend’s performance might fluctuate due to fatigue, psychological factors, or changing conditions (crowd noise, muscle memory, etc.). If the probability of success varies from shot to shot, then modeling all shots with a single static θ may be inappropriate.
A potential pitfall is overconfidence in the posterior if we ignore the dependence among shots. If your friend’s skill changes over time, the posterior might incorrectly concentrate too heavily around certain θ values. One workaround is to extend the model to account for time-varying parameters, such as a hierarchical or state-space model, which allows θ to evolve over time. Another approach is to group shots into smaller segments under the assumption that θ is approximately constant within each segment but can change between segments.
An edge case scenario is when your friend’s shooting form radically changes mid-experiment (for instance, shifting from a one-handed to a two-handed free throw style). A standard Bernoulli model with a single θ would be invalid. In such a case, a Bayesian change-point model could be used to detect and adapt to shifts in the performance probability.
How might we extend this approach to include multiple friends each taking shots?
If we have multiple friends, each potentially having a different success probability θi for free throws, we can place a prior distribution on each θi and observe each friend’s shot outcomes. A simple approach is to assume the friends are exchangeable and use a common prior for all θi. Then, for each friend’s data (si successes out of ni shots), the posterior for that friend’s θi can be updated accordingly.
A possible pitfall is failing to pool information across friends when we actually do have reason to believe there is some commonality in skill level. In such a scenario, a hierarchical (multilevel) Bayesian model is often used, where each friend’s skill parameter θi is drawn from a hyper-distribution that itself has unknown parameters. This approach shares statistical strength across friends, especially if some have only a few observations. However, a mismatch between the assumed common structure and reality might lead to inaccurate estimates if, for example, one friend is extremely skilled while another is not.
What if the data set is large enough that the prior has minimal influence?
In a large-sample regime—imagine your friend takes thousands of shots—Bayesian updating typically results in the likelihood dominating the posterior. When the likelihood is highly peaked due to a large n, the final posterior depends less on the exact shape of the prior.
A potential misunderstanding arises if one concludes the prior is “unimportant” in all cases. While for large n the posterior is robust to moderate changes in the prior, in situations with fewer data points, an informative prior can have significant effects. Another subtlety is that if the prior is badly misspecified (e.g., it places almost zero mass near the true parameter), it can still skew the posterior even for relatively large data sets, though such severe mismatches are less common in well-chosen priors.
How would the inference change if the prior interval was different, say (0, 1) instead of (0.25, 0.75)?
If we used a broader prior range, such as (0, 1), the posterior would have a support covering the entire [0, 1] interval. This would likely change the posterior shape because we would be assigning some probability mass to θ < 0.25 and θ > 0.75. If the friend’s data strongly suggests θ around 0.6, then expanding the prior domain might not drastically shift the posterior mean or mode, but it can affect the tails of the distribution.
A potential issue is if we initially restricted the prior range to (0.25, 0.75) because we were certain your friend’s true skill is not outside that range. In that case, using (0, 1) might unhelpfully waste mass on implausible θ values (like 0.05 or 0.95) if such extremes really aren’t relevant. On the other hand, if we were wrong in restricting θ to (0.25, 0.75) (maybe your friend is a world-class 90% shooter), then the narrower prior would heavily bias our inference.
What if the observed data show fewer (or more) successes than the prior mode suggests?
If the observed data deviate significantly from what the prior suggests, the posterior might shift away from the prior mode quite substantially, highlighting a conflict between prior assumptions and the evidence from data. In practice, this conflict is healthy to see because it forces a re-evaluation of whether the prior was too dogmatic.
A common pitfall is ignoring the possibility that the friend’s skill could actually be much higher or lower than assumed. If the data show your friend hitting 9/10 shots, the posterior might concentrate above 0.7, contradicting an overly narrow prior. Conversely, if your friend hits only 2/10, the posterior might concentrate below 0.3, challenging the prior’s assumption that θ was at least 0.25. In Bayesian practice, it is vital to check the sensitivity of your posterior to your prior assumptions and possibly revise the prior if the mismatch is too large.
How would you handle the situation if some attempts were missing or not observed?
Real-world data can sometimes be incomplete. Suppose you only observed 8 shots and know there were 2 unobserved attempts whose outcomes you don’t know. If we assume those missing attempts are missing at random, one could either:
Treat them as latent variables and integrate them out in a fully Bayesian approach. You would effectively sum (or integrate) over the possible outcomes of the unobserved shots, weighting by their probabilities under the prior.
Use multiple imputation techniques: repeatedly simulate plausible outcomes for the missing data, update the posterior for each imputed scenario, and average.
A subtle pitfall is if the missing attempts are not missing at random; for example, your friend might have hidden the attempts where he did poorly. In that case, the data are biased and a naive approach would yield an overly optimistic posterior. You would need to model the missingness mechanism explicitly—perhaps factoring in the probability of a missing attempt being more likely if it was a miss.
Could outliers in observed data affect the posterior inference?
In a Bernoulli trial, an “outlier” might be an unexpected streak of hits or misses. Though Bernoulli data do not typically have outliers in the same sense as continuous data, you can still get surprisingly extreme runs. In a Bayesian framework, a streak of successes would tilt the posterior toward higher θ, which may or may not match the prior belief.
One pitfall is over-reacting to short bursts of unusual performance if one’s prior is not designed to accommodate transient changes. With a static θ assumption, the posterior might lurch significantly after a short hot streak. For a more robust approach, you might consider dynamic models or place a prior that allows for momentary deviations.
How would the credible interval change if we used a highest-posterior-density (HPD) interval instead of a percentile-based interval?
A 95% highest-posterior-density interval is defined as the smallest interval on θ such that the integral of the posterior density within that interval is 0.95. This can differ from the equal-tailed credible interval, especially if the posterior is skewed or multimodal.
If the posterior is sharply peaked and unimodal, both intervals might be nearly identical. But if the posterior has a skew or multiple peaks, the HPD might skip over low-density regions, producing an interval that excludes less likely subranges. A potential pitfall is incorrectly assuming that the 2.5th and 97.5th percentiles always yield the most probable region. In truly asymmetric or bimodal posteriors, the HPD interval could look quite different (maybe it even splits into multiple disjoint subintervals in extreme cases).
What if θ = 0.5 was truly the exact success probability—would we always recover that from the posterior?
In theory, if θ = 0.5 is the true probability, a large number of Bernoulli trials would concentrate the posterior tightly around 0.5. However, with a small sample (e.g., 10 shots), randomness can push the observed data away from 5/10 successes.
A subtle real-world pitfall is overconfidence with small sample sizes. Even though the true θ might be 0.5, you might observe, say, 7/10 successes. The posterior can then be centered around a value > 0.5. As data grows, the posterior should converge near the true parameter (by Bayesian consistency) provided the model is well-specified and the prior is not pathological. But in real-world small-sample scenarios, random chance and the prior shape can significantly sway the posterior.
How do we interpret the Bayesian “confidence interval” compared to a frequentist confidence interval?
The 95% Bayesian credible interval is the range of parameter values within which we have 95% posterior probability that θ lies. By contrast, a 95% frequentist confidence interval is derived from a procedure that ensures 95% coverage over repeated experiments, but does not directly give a probability statement about θ itself.
A common pitfall is to use “probability that θ is in this interval” language for frequentist intervals, which is incorrect from a strict frequentist standpoint. Meanwhile, in Bayesian analysis, we can directly interpret the credible interval as a statement about our degree of belief. A subtlety arises if the prior is strongly informative or not aligned with a frequentist viewpoint. In that case, the Bayesian credible interval might not coincide well with what a frequentist would compute.