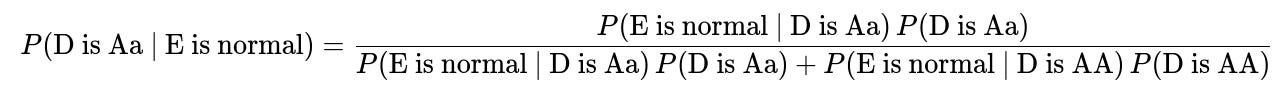ML Interview Q Series: Bayesian Inference for Genetic Carrier Probability Based on Descendant's Normal Phenotype.
Browse all the Probability Interview Questions here.
If E is observed to be phenotypically normal, what is the likelihood that D carries one normal gene and one mutated gene?
Comprehensive Explanation
A common way to tackle problems about the probability that an individual (D) is a carrier of a mutated gene, given that their descendant (E) appears normal, is to use conditional probability. In typical Mendelian genetics, a mutated gene that is recessive will only manifest its phenotype if an individual has two copies of that recessive (mutated) allele. An individual who has one normal (dominant) allele and one mutated (recessive) allele is often referred to as a “carrier” or heterozygote. This person does not usually exhibit the disease phenotype but can pass the mutated allele to offspring.
When we say “E appears normal,” in the context of recessive diseases, it means E is either homozygous normal (both alleles normal) or a carrier (one normal and one mutated allele). The fact that E is not homozygous recessive (both alleles mutated) adds information that updates how likely it is that D is a carrier. The standard framework to quantify this is Bayes’ Theorem, which helps us update the prior probability of an event (D being a carrier) in the light of new evidence (E is phenotypically normal).
The Bayesian Formula
The probability that D is a carrier (Aa), given that E is normal, can be written in its simplest form using Bayes’ Theorem:
Here is a breakdown of the terms in plain text format:
P(D is Aa) is the prior probability that D carries one normal and one mutated allele before we know anything about E. This often depends on family history, population genetics data, or other background information.
P(D is AA) is the prior probability that D is homozygous normal (both alleles normal) before we know about E.
P(E is normal | D is Aa) is the probability that E turns out normal given that D is a carrier. This can be computed from Punnett squares if we also know or assume the other parent's genotype or carrier probability.
P(E is normal | D is AA) is the probability that E turns out normal given that D is homozygous normal. This is typically quite high, but depends on the other parent’s genotype.
By applying this formula, we obtain the posterior probability that D is a carrier under the condition that E is phenotypically normal. In many textbook genetics scenarios, if there is a known family pattern and some standard assumptions (e.g., the partner of D has a certain probability of being a carrier, or is fully normal, etc.), the resulting probability might simplify to a classic fraction such as 2/3, 1/2, or 1/3, depending on the specifics.
Practical Reasoning
In a real-world interview or problem-solving context, you might be given extra details:
Which side of the family has a history of the disease.
Whether the other parent of E is known to be normal or also has some carrier probability.
Whether there is any information about additional siblings.
Whether the disease is fully penetrant or if there is incomplete penetrance.
Armed with these details, you would typically:
Define the prior probabilities (for example, if D’s parent was known to be a carrier, or if D has an affected sibling, etc.).
Use the Punnett square or direct probability calculations to find the probability that E is normal under each possible genotype of D.
Plug these values into Bayes’ Theorem.
Potential Pitfalls
One subtlety is making sure you distinguish between “E is normal genetically” (i.e., homozygous normal) and “E is normal phenotypically” (could be homozygous normal or heterozygous carrier). Many times, “normal” simply means “unaffected,” which includes both homozygous normal and heterozygous genotypes if the gene is recessive. This distinction is essential for computing P(E is normal | D is Aa) correctly.
Another pitfall is forgetting to factor in the genotype (or the probability distribution of genotypes) of E’s other parent. If the other parent also has a certain chance of being a carrier, it may allow for E to be homozygous recessive in some fraction of cases, which then changes the probability that E appears normal. Always clarify both parents’ genetic statuses to get an accurate conditional probability.
Follow-Up Questions
How do we calculate P(E is normal | D is Aa) if we do not know the other parent's genotype?
It is often necessary to specify an assumption about the other parent. For example, if the other parent is definitely not a carrier (known homozygous normal), then any child from D (if D is Aa) will always receive at least one normal allele and thus cannot be aa. In that case, E is guaranteed to appear normal if one parent is AA. If, however, there is a known probability q that the other parent is also Aa, then P(E is normal | D is Aa) must be computed by enumerating the possible child genotypes (AA, Aa, aa). You would do this via Punnett squares:
If both parents are Aa, the child genotype probabilities are 1/4 (AA), 1/2 (Aa), 1/4 (aa).
The probability of being phenotypically normal is (1/4 + 1/2) = 3/4.
You then weigh this against the prior probability that the other parent is Aa or AA, accordingly.
Why does the probability sometimes simplify to 2/3 in standard genetics problems?
A well-known textbook scenario is when D is known to be unaffected but has an affected sibling. In many classic genetics questions, that unaffected status implies that D cannot be aa, but could be either AA or Aa. Under autosomal recessive inheritance, if the parents are both carriers (Aa), then each child has a 1/4 chance of being aa, a 1/2 chance of being Aa, and a 1/4 chance of being AA. Conditional on being unaffected (not aa), the probability of being Aa among unaffected children is (1/2) / (1/2 + 1/4) = 2/3. Then, observing that D has a normal child (E) can shift or maintain the probability, depending on the genotype of the partner and other details.
What if new mutations or incomplete penetrance are possible?
Real genetic scenarios can be more complicated:
New mutations mean that an allele might spontaneously mutate in the germline of a parent. This modifies the probability calculations since even an “AA” parent can produce a mutated allele.
Incomplete penetrance means that some individuals who have two mutated alleles might not show the disease phenotype at all, or a carrier might show partial expression. In that case, “E appears normal” is not as straightforward, because some fraction of aa individuals might not manifest overt signs. The formulas for P(E is normal | D is Aa) or P(E is normal | D is AA) must then account for the probability that an aa genotype escapes detection phenotypically.
Can we implement a quick check of these computations in code?
You can do so with a small Python snippet that calculates probabilities. For instance, if you want to systematically explore the different assumptions about parent genotypes and compare outcomes for E, you could do something like:
def probability_d_carrier_given_e_normal(p_carrier_d, p_carrier_other, p_recessive_penetrance=1.0):
"""
p_carrier_d: prior probability that D is Aa
p_carrier_other: prior probability that other parent is Aa
p_recessive_penetrance: probability that aa phenotype actually manifests. By default 1.0 for full penetrance.
"""
import itertools
# We consider parent D: could be AA or Aa
# We consider other parent: could be AA or Aa
# We'll enumerate child genotype probability and whether child is normal or not.
# prior_d_Aa = p_carrier_d
# prior_d_AA = 1 - p_carrier_d
# prior_o_Aa = p_carrier_other
# prior_o_AA = 1 - p_carrier_other
# Probability child is normal given each combination:
# 1) D = AA, other = AA => child always AA => normal
# 2) D = AA, other = Aa => child 1/2 AA + 1/2 Aa => always normal
# 3) D = Aa, other = AA => child 1/2 AA + 1/2 Aa => always normal
# 4) D = Aa, other = Aa => child genotype distribution: 1/4 AA, 1/2 Aa, 1/4 aa => normal with prob 3/4 (if full penetrance)
# Then apply Bayes.
# This code is a simplified placeholder for demonstration, not a complete Bayesian update over many scenarios.
import math
# Probability D=AA, other=AA => child normal prob 1
p_dAA_oAA = (1 - p_carrier_d) * (1 - p_carrier_other)
p_normal_given_dAA_oAA = 1.0
# Probability D=AA, other=Aa => child normal prob 1
p_dAA_oAa = (1 - p_carrier_d) * p_carrier_other
p_normal_given_dAA_oAa = 1.0
# Probability D=Aa, other=AA => child normal prob 1
p_dAa_oAA = p_carrier_d * (1 - p_carrier_other)
p_normal_given_dAa_oAA = 1.0
# Probability D=Aa, other=Aa => child normal prob 3/4 if fully penetrant
p_dAa_oAa = p_carrier_d * p_carrier_other
p_normal_given_dAa_oAa = 3/4 * p_recessive_penetrance + (1.0 - p_recessive_penetrance) # if partial penetrance, adjust
# Weighted sum for overall probability(E normal)
total_prob_e_normal = (
p_dAA_oAA * p_normal_given_dAA_oAA +
p_dAA_oAa * p_normal_given_dAA_oAa +
p_dAa_oAA * p_normal_given_dAa_oAA +
p_dAa_oAa * p_normal_given_dAa_oAa
)
# Probability that (D is Aa AND E normal)
# We'll treat scenario 3) + scenario 4) for the fraction that yields E normal
prob_D_Aa_and_E_normal = (
p_dAa_oAA * p_normal_given_dAa_oAA +
p_dAa_oAa * p_normal_given_dAa_oAa
)
# Posterior probability
posterior = prob_D_Aa_and_E_normal / total_prob_e_normal
return posterior
# Example usage:
posterior_example = probability_d_carrier_given_e_normal(p_carrier_d=0.5, p_carrier_other=0.5)
print("Posterior Probability (D is Aa | E normal) =", posterior_example)
In a real setting, you would tailor the initial probabilities and incorporate any additional data about family history, penetrance, or repeated offspring outcomes.
All of these details highlight the importance of carefully enumerating possibilities and applying Bayesian updates. In an interview setting, showing an understanding of these probability rules and the subtleties of genetics (such as phenotypic vs. genotypic normality) will demonstrate a strong command of both statistical reasoning and domain knowledge.
Below are additional follow-up questions
How does our calculation change if there is a possibility of misdiagnosing E’s phenotype?
A major assumption in most inheritance problems is that “E appears normal” means E was correctly evaluated as unaffected. However, in real-world scenarios, especially with subtle conditions, mild forms of the disease can be overlooked. This possibility of misdiagnosis affects the probability that E is truly homozygous normal or heterozygous.
If there is a probability r that E is incorrectly labeled normal (when in fact E might be affected but undetected), we must integrate r into our conditional probability. Specifically, we replace P(E is normal | genotype) with [P(correct diagnosis) * P(true normal | genotype) + P(incorrect diagnosis) * P(false normal | genotype)]. This modification can significantly change the posterior probability that D is a carrier, especially if r is not negligible. The key pitfall is failing to recognize that diagnostic errors add uncertainty to the observed phenotype, thus skewing the inference about parental genotypes.
Edge case:
If r is high (meaning frequent misdiagnoses), E’s observed normal phenotype may offer much less information about whether D is a carrier or not.
If r is practically zero (extremely accurate diagnostics), the misdiagnosis factor can be safely ignored in the Bayesian update.
How would the inference process change if the disease is X-linked instead of autosomal recessive?
When the mutated allele is on the X chromosome (for X-linked recessive traits), the inheritance pattern changes. Males have only one X chromosome, so a single mutated X results in the disease phenotype. Females, on the other hand, need two mutated copies to be fully affected under a classic X-linked recessive assumption. For a question about D having one normal and one mutated gene, we must consider D’s sex and E’s sex:
If D is female and the trait is X-linked recessive, D can be a carrier if one of her X chromosomes is mutated. E’s phenotype depends on which X chromosome E inherited (if E is male, then E has a high chance of showing the disease if he inherited the mutated X).
If D is male, the notion of “carrier” is generally not used in the same sense for X-linked recessive diseases, because a single mutated X in a male typically leads to an affected phenotype.
A major pitfall is failing to differentiate between autosomal and X-linked recessive patterns. This leads to incorrect assumptions about how likely E is to appear normal. For instance, if E is male and unaffected, that strongly suggests he did not inherit a mutated X from a carrier mother. Conversely, if E is female, the normal phenotype might still allow for a carrier genotype.
Edge case:
Incomplete penetrance in X-linked conditions where carriers might show mild or partial symptoms.
Skewed X-inactivation in females could cause some heterozygous females to exhibit disease symptoms, complicating the simple classification of “carrier but normal.”
What if we have genetic testing available for some of the family members?
In contemporary genetic counseling, direct testing of an individual’s genotype often becomes available. Suppose we have partial information: perhaps a sibling of D underwent genetic testing or a parent of D tested positive for carrier status. In that scenario, we refine the prior probabilities:
P(D is Aa) might shift if we know exactly which allele the parent carried, or if other siblings’ genotypes have been definitively identified.
If we can do a direct test on D, then this entire question becomes moot—there would be no need for probabilistic inference. However, if only partial testing is done on extended relatives, we incorporate that data using Bayesian networks or standard conditional probability updates.
The pitfall arises when partial testing results are misinterpreted as certain knowledge about D. For example, testing D’s sibling who is a carrier does not guarantee that D is also a carrier. It only increases or decreases D’s probability depending on how many siblings are tested, who turned out to be carriers, and so on.
Edge case:
If the tested parent reveals a new mutation not inherited from grandparents, that might alter the baseline assumption that it came from a longstanding family trait.
If mosaicism is present (where a parent has a mixture of mutated and normal cells), probabilities can shift dramatically.
How do repeated independent observations of normal children from D affect the posterior probability that D is a carrier?
Observing E as normal gives us one piece of evidence that D might or might not be a carrier. If D has multiple children, and each child appears normal, this accumulates evidence. Under standard assumptions of independence (each child’s genotype is drawn independently from the parents’ genetic makeup), the probability that all children are normal grows smaller if D is indeed a carrier, compared to if D is homozygous normal.
Mathematically, we can apply a series of updates after each normal child, or multiply the probabilities directly if we assume identical conditions for each child. Each time we see an additional normal child, the posterior probability that D is Aa tends to drop, reflecting the unlikeliness of repeatedly producing unaffected offspring if D truly carried a mutated allele.
A pitfall is forgetting to treat each child’s outcome as an independent trial (conditional on D’s genotype and possibly the other parent’s genotype). Also, the assumption of independence can be violated by environmental factors or by correlation in genetic events (e.g., certain recombination patterns, selection biases).
Edge case:
If a child is not known for certain (e.g., extremely young or no thorough examination yet), that child’s “normal” status might not carry full weight.
If the other parent is also a carrier, the chance of a normal child each time is smaller, so observing multiple normal children drastically updates the posterior probability that D is a carrier.
Does the frequency of the mutated allele in the general population affect the calculation?
When no family history is fully available, or when there is only partial pedigree information, we might rely on population-level carrier frequencies. Suppose the mutated allele has a low prevalence p in the population, and we have no specific knowledge of family history other than E being normal. In that case, we might set the prior P(D is Aa) to 2p(1-p) (the Hardy-Weinberg approximation) or some adapted probability if we know more about D’s ancestry.
A pitfall is using population frequencies incorrectly. For instance, the presence of a confirmed case in the immediate family modifies the prior dramatically and overrides the naive population-level estimate. Another common slip is ignoring the fact that population-level data might be stratified by ethnicity or geographic location, so the actual relevant frequency might differ from the global average.
Edge case:
If p is extremely small, the probability that D is a carrier might be negligible unless the family history points otherwise.
In consanguineous marriages, the local effective allele frequency for the family can be significantly higher than the general population frequency, thus changing the baseline prior.
How do we handle the situation where D might carry more than one possible mutation for the same gene?
Certain conditions, like cystic fibrosis, can be caused by different mutations in the same gene. If D might carry any of several mutations, each with its own prevalence, the analysis must sum or integrate over all possible mutations. In other words, D could be “compound heterozygous,” with different mutated alleles on each chromosome. For a child to be affected, E would need to inherit at least one disease-causing allele from each parent in a pattern that leads to a recessive phenotype.
The pitfall is oversimplifying a disease with many known pathogenic variants into a single “mutated vs. normal” scenario. Sometimes, certain mutations are milder, leading to partial phenotypes, while others are severe. This variation impacts the probability that E is phenotypically normal if E inherits different combinations of mutated alleles.
Edge case:
If one particular mutation has incomplete penetrance or partial dominance, the child’s phenotype might be less predictable, requiring more nuanced probability modeling.
If multiple mutations exist but only one is prevalent in a specific family lineage, the analysis can simplify by ignoring the rarer mutations outside that lineage.
Can environmental or epigenetic factors influence the appearance of E’s phenotype and thus change the inference about D?
Even with classical Mendelian inheritance, environment and epigenetic modifications can influence whether a condition manifests, especially if the trait has some gene-environment interaction. For instance, a genetically recessive allele might not lead to a full disease phenotype if the individual adheres to certain dietary restrictions or environmental exposures are minimized.
In this context, “E appears normal” might not fully guarantee that E is genetically unaffected—rather, it might indicate that E has not encountered the environmental trigger. If we know that the environment is protective, the probability of E showing a disease phenotype is reduced even if E is aa. This distorts our usual probability that “aa => definitely affected.”
Pitfall:
Using a simplistic model that equates genotype with phenotype can lead to erroneous conclusions when major environmental or epigenetic factors are at play.
Overlooking the possibility that E might be genetically affected but remains asymptomatic due to environmental reasons can inflate the probability that D is not a carrier.
Edge case:
If the environment changes (say E moves to a region where a certain deficiency or toxin is more common), E might start to show the disease later, revising the entire inference about D’s carrier status.
Some epigenetic modifications might be inherited across generations, adding further complexity.
How might non-random mating or population structure alter our assumptions?
Bayesian calculations that assume independence and Hardy-Weinberg proportions rely on random mating in a large population. However, in many real contexts, mating might not be random (for example, certain communities with higher rates of consanguinity or individuals selecting partners with similar backgrounds). This can significantly raise the likelihood that both parents carry the same rare mutated allele.
If we suspect or know non-random mating, the prior probability that the other parent is a carrier might be higher than the general population figure, leading to a higher posterior that D is also a carrier. Ignoring such population structure is a frequent pitfall.
Edge case:
In small isolated populations, the same recessive disease alleles might be circulating at much higher frequencies, making standard population-level estimates too low.
Genetic drift in a small population or founder effects in certain subpopulations can drastically shift prior probabilities of carriers.