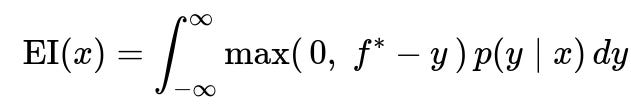ML Interview Q Series: Bayesian optimization uses expensive black-box cost functions; what surrogate or acquisition strategies improve search efficiency?
📚 Browse the full ML Interview series here.
Hint: Gaussian processes with EI or Thompson Sampling are common
Comprehensive Explanation
Bayesian optimization is an iterative technique used to optimize expensive black-box functions. In hyperparameter tuning, we view the model training/validation process as a function that is extremely costly to evaluate. We need to minimize or maximize this function using as few function evaluations as possible. Bayesian optimization accomplishes this by building a surrogate model of the objective and then deciding where next to sample using an acquisition strategy.
Surrogate Models
A surrogate model is a probabilistic model that approximates our expensive objective. Common surrogate models:
Gaussian Processes (GPs): A powerful non-parametric model that provides a posterior mean and variance of the function at any point. It assumes a prior (often a kernel-based function) over the function space and updates it with observed data.
Random Forests or Tree Parzen Estimators (TPE): Sometimes used when GPs do not scale well in high-dimensional spaces or when the objective function exhibits strong non-stationarities.
Neural Network Surrogates: Useful if you want a flexible model that might capture complex interactions, though GPs remain standard for many use cases.
Acquisition Functions
An acquisition function guides the search by quantifying the utility of evaluating the objective at each possible point. Common acquisition strategies include:
Expected Improvement (EI)
Probability of Improvement (PI)
Upper Confidence Bound (UCB)
Thompson Sampling
Entropy Search / Knowledge Gradient
They balance exploration (sampling where the model is uncertain) and exploitation (sampling where the model predicts high performance).
Expected Improvement (EI)
Expected Improvement is one of the most popular acquisition functions. EI compares the predictive distribution at each candidate point against the best observed value so far (denoted f^*) and calculates the expected amount of improvement. The core formula for EI can be expressed as:
Here:
f^* is the current best (minimum or maximum) observed function value, depending on whether you are minimizing or maximizing.
y is a possible function value at x as predicted by the surrogate.
p(y | x) is the predictive distribution of y given x from the surrogate model.
If the best observed value so far is f^, the quantity f^ - y represents how much better f^* is than y. The integral computes the expected amount of improvement relative to f^*, weighted by the model's belief distribution.
Thompson Sampling
Thompson Sampling picks samples based on drawing random realizations from the surrogate model posterior. At each iteration:
Sample a function from the posterior distribution of your surrogate model.
Choose the next point x that optimizes this sampled function.
Evaluate at x and update the model with the new observation.
This approach naturally balances exploration and exploitation because random draws reflect the current model’s uncertainty.
Upper Confidence Bound (UCB)
In UCB-based methods, we optimize mean(x) - beta * std(x) (or mean(x) + beta * std(x), depending on whether we want to minimize or maximize). The parameter beta controls the trade-off between exploring uncertain regions (where std is high) vs. exploiting promising areas (where mean is good).
Practical Implementation
Below is a minimal Python-like pseudocode illustrating the Bayesian optimization loop using a GP surrogate and Expected Improvement. This is a conceptual example (not tied to any specific library):
import numpy as np
from some_gp_library import GaussianProcessRegressor
def objective_function(params):
# Costly black-box function we want to minimize or maximize
return expensive_evaluation(params)
def expected_improvement(x, model, f_best):
# Suppose model.predict(x, return_std=True) returns (mean, std)
mu, sigma = model.predict(x.reshape(1, -1), return_std=True)
# Compute EI as described above or via closed-form formula
# For simplicity, a direct closed-form approach using the normal distribution can be used
# This function returns a scalar EI at point x
return EI_value
# Bayesian Optimization Loop
X_observed = [] # Observed parameter locations
Y_observed = [] # Observed objective values
# Initialize with random samples
X_observed = np.random.rand(5, param_dimension)
Y_observed = [objective_function(x) for x in X_observed]
model = GaussianProcessRegressor()
for iteration in range(num_iterations):
model.fit(X_observed, Y_observed)
f_best = min(Y_observed) # Or max, depending on your problem
# Propose candidate points (random or a grid or by optimization of acquisition function)
candidate_points = propose_points()
# Evaluate EI at each candidate
ei_values = [expected_improvement(x, model, f_best) for x in candidate_points]
# Select best point
x_next = candidate_points[np.argmin(ei_values)] # or argmax if you define EI accordingly
# Evaluate objective
y_next = objective_function(x_next)
# Update
X_observed = np.vstack((X_observed, x_next))
Y_observed.append(y_next)
What About Other Surrogate Models?
Though Gaussian processes are standard, you could use random forests or TPE if your hyperparameter space is high-dimensional or if your objective surface is non-smooth and shows abrupt changes. Neural networks can also serve as surrogates, but they may require more data to train.
Follow-up Questions
How do you choose between different acquisition functions in practice?
One might look at the nature of the objective function, dimensionality, and available computation budget. For relatively smooth objectives in moderate dimensions, EI or UCB with a Gaussian process is standard. If you need a more exploratory approach or have a discrete space with noise, Thompson Sampling can be simpler and effective. In large dimensions or with very noisy evaluations, more specialized techniques or heuristics (like TPE) might perform better.
Can Bayesian optimization handle noise in the objective function?
Bayesian optimization can handle noise through the surrogate model, especially if the model includes a noise term in its likelihood function. Gaussian processes often assume Gaussian noise in observations, so if that aligns with your setting, GP-based Bayesian optimization works well. Alternatively, you could use a surrogate that is robust to noise (e.g., certain ensemble methods) and an acquisition function that accounts for uncertainty from both noise and model inaccuracy.
What are potential challenges in high-dimensional hyperparameter spaces?
As dimensionality grows, Gaussian processes can struggle because kernel-based methods may require a large number of samples to get a good model fit. High-dimensional spaces can also make the acquisition function optimization itself challenging. Practitioners often reduce the search space by selecting fewer hyperparameters or applying dimensionality reduction. Methods like random embeddings or TPE can sometimes scale better.
How do you implement these methods if the objective function is non-stationary or changes over time?
Standard Bayesian optimization typically assumes a stationary objective (i.e., it does not shift as you gather data). If the objective drifts over time, you might use a time-weighted or windowed approach that discounts older samples, or you could adapt the kernel to account for non-stationarity. There are specialized Bayesian optimization frameworks (e.g., dynamic Bayesian optimization) that update the prior or surrogate model to handle changing conditions.
How do you handle discrete or categorical hyperparameters?
Discrete or categorical variables can be treated in two ways:
Mixed Surrogate Models: Use specialized kernels or expansions in Gaussian processes or TPE that handle categorical inputs gracefully.
One-Hot Encoding: Convert categories into one-hot vectors, though this can be less efficient for high-cardinality categorical variables.
Tree-based surrogates (like random forests or TPE) often handle categorical variables more naturally than standard Gaussian processes.
Could you explain the difference between Probability of Improvement (PI) and Expected Improvement (EI)?
Probability of Improvement simply calculates the probability that a given point will improve over the current best. It does not consider how much improvement. Meanwhile, EI considers both the probability of improvement and the magnitude of that improvement. Typically, EI encourages the algorithm to sample in areas that yield a higher overall expected gain, whereas PI might focus too heavily on points that have a small but non-negligible chance to just barely beat the best observed value.
Are there any risks or failure modes of Bayesian optimization?
In practice, issues can arise if:
The search space is enormous and GP-based methods become computationally expensive.
The surrogate model is mis-specified (e.g., kernel choice not matching the true behavior).
The objective has high noise or abrupt discontinuities, making learning challenging.
There is insufficient diversity in initial points, leading to suboptimal local minima exploration.
Addressing these requires carefully chosen initial sampling, hyperparameter tuning of the surrogate, and possibly switching to alternative surrogates that cope well with noise and discontinuities.
Below are additional follow-up questions
How do you incorporate the evaluation cost or runtime into the Bayesian optimization process?
When the time to evaluate the objective function varies significantly across different hyperparameter configurations, you might want to factor that cost directly into the acquisition strategy. One approach is to modify the surrogate model to predict not only the performance metric but also the resource cost (like computation time). You could incorporate a multi-output model (one output for performance, another for cost), or use a composite objective that balances performance against evaluation cost. Then, instead of maximizing or minimizing purely the performance metric, you focus on an acquisition function that also accounts for how long each new query would take.
Potential pitfalls arise if the cost model is poorly learned (for instance, if certain hyperparameters occasionally spike in runtime due to external factors like system load). Handling outliers in runtime can be tricky, requiring robust modeling strategies. Another subtle issue is that cost might be correlated with certain hyperparameters (e.g., larger batch sizes might reduce training iterations but increase memory usage), so the optimization must capture such interactions carefully.
How do you handle multi-objective Bayesian optimization where you have more than one metric to optimize?
In multi-objective settings, you are typically interested in finding a set of Pareto-optimal solutions rather than a single optimum. You might use vector-valued Gaussian processes or train separate surrogate models for each objective. Then you apply an acquisition function adapted to multi-objective goals, such as Expected Hypervolume Improvement (EHI). The principle is similar to single-objective Bayesian optimization but requires strategies to evaluate improvement in multiple objectives simultaneously.
A key challenge is that as the number of objectives grows, balancing each objective’s requirements becomes complex. Defining the trade-off between objectives (e.g., weighting them, or focusing on a region of the Pareto front) can be a stumbling block. Furthermore, scaling multi-objective Bayesian optimization to high-dimensional input spaces can be computationally expensive, often requiring specialized heuristics or approximations.
How do you parallelize Bayesian optimization when you can evaluate multiple points simultaneously?
If you can evaluate the objective at several parameter configurations in parallel, you want to choose multiple candidates in each iteration rather than a single point. One approach is batch Bayesian optimization, where the acquisition function is extended to propose a set of points by considering correlations among those points. For instance, you might use batch Expected Improvement, which accounts for the fact that evaluating multiple locations will reduce uncertainty collectively. Alternatively, a heuristic approach is to pick one point by your standard acquisition function, then temporarily update the surrogate model with a “fantasy” observation (some predicted outcome) for that point, then pick the next point, and so forth, until you have the desired batch size.
One pitfall is that naive approaches might end up suggesting multiple points that are very similar or located in the same region of the parameter space. To avoid this, you must ensure that the acquisition function or the sampling heuristic includes a diversity mechanism. Another subtlety is that real-world computation resources might have different throughput for different parameter settings, so you may not truly evaluate them all “in parallel,” leading to scheduling or resource-allocation complexities.
What if you have constraints on the hyperparameters or the model’s outputs during optimization?
Constrained Bayesian optimization introduces additional terms to capture feasibility. You might train a separate surrogate model to predict whether a constraint is satisfied (e.g., memory constraints, accuracy above a threshold, or latency below a certain bound). Then you modify the acquisition function to favor only the feasible region of the parameter space.
A tricky edge case arises when constraints are “soft” or only partially known. You might end up with a scenario where the feasible region is very small or disjoint, making it difficult for standard kernels to capture. Another subtlety is ensuring that early infeasible samples provide enough signal for the surrogate to learn the boundary of feasibility. If the constraints are dynamic over time (e.g., changed resource limits), the surrogate models must adapt quickly, or you risk collecting wasted samples in infeasible regions.
How do you handle partially observed or streaming feedback during optimization?
Sometimes you do not get a single scalar score but a stream of data points, or partial feedback (like success/failure signals over time). You could model this scenario by continuously updating the surrogate model whenever partial information arrives. For instance, if you see that intermediate training metrics look poor, you might stop that run early (early stopping) and incorporate that partial observation into your model.
Pitfalls arise because partial feedback can be noisy or might not be fully indicative of the final outcome (e.g., a model can have a slow start in training and then catch up). Ensuring the surrogate does not overfit to early partial signals is crucial. You might need a carefully designed prior or a custom kernel that treats early partial metrics differently from final measurements. Another edge case is handling asynchronous updates when different runs finish at unpredictable times.
How can you exploit a cheaper proxy or approximate function before doing expensive evaluations?
A common real-world approach is to have two levels of evaluation: a cheaper, approximate metric (for instance, a model trained for fewer epochs or on a smaller dataset) and a more expensive, accurate metric (the full training). You might use multi-fidelity Bayesian optimization, where you build separate surrogates for different fidelities or treat fidelity as an input dimension. Then your acquisition function decides when it is worth moving from cheaper evaluations to the costly, high-fidelity ones.
A subtlety is that the correlation between low-fidelity and high-fidelity results might be weak in some regions of the parameter space. This mismatch can lead to misleading conclusions if the surrogate over-relies on lower-fidelity data. Managing the trade-off between sampling cheaply in many places vs. more expensively in a few carefully selected configurations is a key challenge. Another pitfall is the possibility that some hyperparameters scale differently at low fidelity compared to high fidelity (e.g., small learning rates might do fine on fewer epochs but become suboptimal when fully trained).
How do you get confidence intervals or uncertainty estimates on your chosen hyperparameters at the end?
By nature, Bayesian optimization maintains a posterior distribution over the objective function. Once it converges (or once you decide to stop), you can sample from that posterior around the region that the model believes is optimal. This procedure gives you not just a single best hyperparameter set but also a range of plausible near-optimal configurations. You can then analyze the variance in model predictions around these hyperparameters to gauge how sensitive the objective is to small changes.
Pitfalls arise when the surrogate model is overconfident—if it underestimates uncertainty, you might trust a narrow region of hyperparameters too strongly. Conversely, in high-dimensional spaces or with limited data, the model might remain uncertain over large swathes of the space, giving you very broad confidence intervals that are not very informative. Proper calibration of the surrogate model is essential to ensure meaningful confidence intervals.
How do you incorporate prior knowledge or domain expertise into Bayesian optimization?
You can embed domain knowledge in two main ways:
Choice of Kernel: Tailor the kernel in a Gaussian process or the structure in a Bayesian neural network to reflect known smoothness, periodicity, or interactions in the hyperparameters.
Prior Distribution: If you already suspect certain regions of hyperparameters are more likely to yield good performance, you can set a prior that weights these regions more heavily. You might specify a mean function or an initial set of points focusing on that region.
A difficulty is that incorrect or overly aggressive prior knowledge might bias the model and miss better solutions outside the assumed region. Striking the right balance between leveraging domain expertise and allowing the model to discover new possibilities is key. Furthermore, in complex domains (like large-scale deep learning architectures), domain knowledge might be partial or contradictory, so the surrogate model must still maintain enough flexibility to explore.
How do you debug or diagnose situations where Bayesian optimization seems to “get stuck” or fail to improve?
First, check if the surrogate model is fitting the observed data well. You can inspect residual plots or measure predictive error on a hold-out set of evaluations. If the model is consistently wrong or too uncertain, you might need a different kernel or a different surrogate altogether. Next, evaluate your acquisition function in various scenarios to see if it’s leading you repeatedly into the same region of the parameter space.
Another source of trouble is insufficient exploration in high-dimensional or highly non-convex surfaces; you might need to adjust acquisition parameters (like the exploration-exploitation trade-off). Additionally, consider whether the initial design or initialization was too narrow. An edge case arises if the best region is actually on the boundaries or corners of the space, yet the kernel or surrogate prior strongly biases sampling toward the center. In that case, you might explicitly incorporate boundary checks or uniform exploration near edges.
How can Bayesian optimization be adapted if the objective can change over time (dynamic or non-stationary objective)?
Standard Bayesian optimization generally assumes a static objective. If the objective changes (due to concept drift, changes in data distribution, or new constraints), you could apply techniques like:
Sliding Window or Decay: Gradually discount older observations or weigh recent observations more heavily.
Time-Varying Surrogate: Introduce time as an input dimension in the model. This allows the surrogate to learn how the function evolves.
Reset or Partial Reset: Periodically reset the surrogate model if you suspect drastic changes in the objective, ensuring you do not rely on outdated data.
Pitfalls include not recognizing changes quickly enough, which can lead to poor recommendations. Another tricky point is deciding the rate at which old data is discarded—if you do so too fast, you lose potentially relevant historical patterns; if you discard it too slowly, you become unresponsive to genuine shifts in the objective.