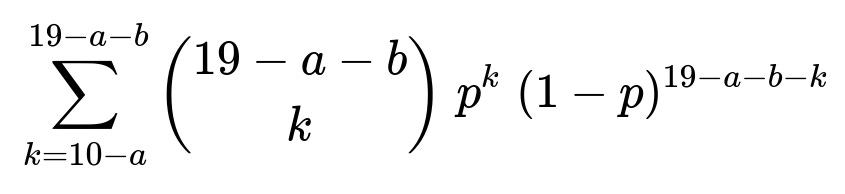ML Interview Q Series: Calculating Win Probability in an Interrupted Game Using Binomial Distribution.

Browse all the Probability Interview Questions here.

Question: Mr. Fermat and Mr. Pascal are playing a game of chance in a cafe in Paris. The first to win a total of ten games is the overall winner. Each of the two players has the same probability of 1/2 to win any given game. Suddenly the competition is interrupted and must be ended. This happens at a moment that Fermat has won a games and Pascal has won b games with a < 10 and b < 10. What is the probability that Fermat would have been the overall winner if the competition had continued? Hint: imagine that another (10 - a) + (10 - b) - 1 games would have been played.

Short Compact solution

We can represent every possible outcome of the remaining 19 - a - b games by all sequences of length 19 - a - b, where each outcome corresponds to a sequence of “win” (for Fermat) or “loss.” Each sequence is equally likely, with probability 1 / 2^(19 - a - b). To determine the probability that Fermat reaches ten total wins first, we need him to secure at least (10 - a) additional wins out of these remaining 19 - a - b games. The probability is therefore

Comprehensive Explanation

Core idea

When the game is interrupted, Fermat has won a games, while Pascal has won b games. Neither has reached 10 wins yet, so to win overall, Fermat needs at least 10 - a additional wins. Similarly, Pascal needs at least 10 - b additional wins. Because the game ends as soon as one player hits 10 wins, in the uninterrupted scenario we only need to count how often Fermat would have eventually reached 10 first.

Counting possible outcomes

We imagine continuing the sequence of games until it becomes certain someone has reached 10 total wins. A useful reframe is to note that once the first of the two players reaches 10 wins, there is no need to play further. However, it is mathematically simpler to suppose that exactly 19 - a - b more games are played, regardless of who wins first, because by the time 19 - a - b games have been played in total, one of them must have hit 10 total wins. Specifically:

• Fermat needs (10 - a) more wins to reach 10.

• Pascal needs (10 - b) more wins to reach 10.

If we account for a total of (10 - a) + (10 - b) - 1 = 19 - a - b games, whoever first reaches 10 wins by or before that point is the overall winner.

Uniform probability over sequences

Each game is a Bernoulli trial with probability 1/2 of Fermat winning and 1/2 of Pascal winning. Hence, all 2^(19 - a - b) possible sequences of wins/losses for these remaining 19 - a - b games are equally likely. We encode a “1” for a Fermat win and a “0” for a Pascal win in each of these hypothetical remaining games.

Determining when Fermat wins

Fermat will have a total of a + k wins if he wins k of the remaining 19 - a - b games. To ensure Fermat ends up with 10 total wins (i.e., a + k >= 10), he needs k >= 10 - a. Because k cannot exceed 19 - a - b, Fermat’s winning condition is k from 10 - a up to 19 - a - b.

Calculating the final probability

The total probability of Fermat winning is the sum of probabilities over all k in the valid range. Each event (where Fermat wins exactly k times in those 19 - a - b games) has probability:

(binomial coefficient (19 - a - b choose k)) * (1/2)^(19 - a - b).

Summing from k = 10 - a up to 19 - a - b yields

which is exactly the probability that Fermat would eventually become the overall winner if play continued.

Intuition check

• If a is much larger than b (i.e., Fermat is just one win away, while Pascal is several wins away), then the lower limit 10 - a is quite small. Most terms in the sum will contribute significantly, meaning that Fermat has a high probability to eventually win.

• If b is close to 10 while a is far from 10, the opposite occurs: 10 - a might be quite large, so only larger values of k matter for Fermat, and the probability that Fermat will eventually win might be relatively small.

Example numeric scenario

• Suppose a = 9 and b = 5. Then Fermat needs only 1 more win (i.e., 10 - 9 = 1), while Pascal needs 5 more wins (i.e., 10 - 5 = 5). The total remaining games considered would be 19 - 9 - 5 = 5. We look at the probability that Fermat wins at least 1 out of those 5 games. That is 1 - P(Fermat wins 0) = 1 - (binomial coefficient (5 choose 0)) * (1/2)^5 = 1 - (1 * 1/32) = 31/32.

• This result aligns with our intuition that Fermat is very close to victory, so he has a very high chance of eventually winning.

Potential Follow-up Questions

How would the formula change if the probability of Fermat winning each game is p instead of 1/2?

If Fermat’s probability of winning a single game is p (and Pascal’s is 1 - p), the same binomial approach applies, but each term in the sum changes accordingly. The probability that Fermat wins exactly k of the next 19 - a - b games would be (binomial coefficient (19 - a - b choose k)) * p^k * (1 - p)^(19 - a - b - k). Then Fermat’s probability to reach 10 total wins before Pascal is:

Could we solve this problem using a negative binomial or a direct counting approach?

Yes, there are formulations involving negative binomial concepts. One way is to observe that Fermat needs (10 - a) additional wins, and Pascal needs (10 - b). You can track how likely it is for Fermat to accumulate (10 - a) wins before Pascal does so. A direct counting approach is also possible by enumerating sequences of wins and losses up to the point when someone hits 10, but the binomial-sum formulation here is typically the cleanest.

What happens if a or b is already 10 or greater?

The question states a < 10 and b < 10, so that scenario is outside the problem’s scope. In practice, if a = 10 (or b = 10) the game would already be over. Hence, no probability computation is needed in that trivial case, as the winner would be certain.

How can we compute this in Python?

Below is a short Python code snippet showing how you might compute this probability using a binomial expression from a standard math library:

import math

def fermat_win_probability(a, b):
    # Number of additional games considered
    n = 19 - a - b
    prob = 0.0
    for k in range(10 - a, n + 1):
        prob += math.comb(n, k) * (0.5**n)
    return prob

# Example usage:
print(fermat_win_probability(a=9, b=5))  # Expecting 31/32 = 0.96875

This code iterates over k from 10 - a to n (which is 19 - a - b) and accumulates the probability. The math.comb function in Python 3.8+ computes binomial coefficients, making it straightforward to implement.

Below are additional follow-up questions

What if the probability of a Fermat win changes dynamically over time rather than remaining constant at 1/2?

In a real-world scenario, player performance might vary over time due to factors like fatigue, changing strategies, or even external conditions. This implies that the probability of Fermat winning each subsequent game could shift as the series progresses.

Answer Explanation:

• When the probability p of a Fermat win is no longer fixed and can change from game to game, the binomial approach used in the original solution is no longer strictly valid. Instead, one would have to account for a sequence of distinct probabilities, say p_1, p_2, ..., p_{n}, where p_i is the probability that Fermat wins the i-th additional game.

• A generalized approach typically involves enumerating all paths in a decision tree or using dynamic programming. One possible approach is to track the probability of reaching a state (x, y), where x is the number of Fermat's wins so far, and y is the number of Pascal's wins. Then one iterates over possible transitions (x, y) -> (x+1, y) or (x, y) -> (x, y+1) with probabilities that depend on the game index.

  This dynamic approach can become computationally expensive if the number of remaining games is large. One must carefully optimize or approximate to handle real-time or large-scale settings.

• A potential pitfall is ignoring the fact that the match ends as soon as someone hits 10 wins. If the probability is changing, you cannot simply sum a fixed number of terms. Instead, you have to truncate the sequences at whichever point the 10th win is reached.

Can we derive a closed-form expression for the sum, or do we need to rely on the cumulative distribution function?

Sometimes, for interview or academic purposes, one might ask if there is a neat closed-form for:

a + k wins out of n = (19 - a - b) trials.

Answer Explanation:

• In many binomial sum problems of the form ∑ [k = M to N] ( C(N, k) * (1/2)^N ), the result can be expressed in terms of the regularized incomplete Beta function or the cumulative distribution function (CDF) for the binomial. A “closed-form” in elementary functions usually does not exist for partial sums of binomial probabilities, so the standard practice is to refer to the binomial CDF or a Beta function.

• Specifically, one might express the probability that Fermat ends with at least 10 total wins as: 1 - F_binomial( p, n, m ), where F_binomial is the CDF for the binomial distribution with parameters n and p. However, this is more a “special function” expression rather than a simple closed-form like a polynomial or rational expression.

• A pitfall is to assume that a neat algebraic simplification always exists. In practice, you would likely compute this numerically using library functions.

Why do we specifically consider 19 - a - b more games, and not continue beyond that? Couldn’t it be that no one has reached 10 by the time we exhaust 19 - a - b games?

At first glance, you might wonder if the total of 19 - a - b extra games might still not see either player get to 10 wins.

Answer Explanation:

• Notice that a + b total wins have already been obtained, and both a < 10 and b < 10. The maximum combined wins either player can need is (10 - 1) + (10 - 1) = 18 if they both only had 9 wins. But in that scenario, a + b would already be 18, leaving just 1 more game needed to decide the final winner.

• In general, if one player requires (10 - a) wins and the other (10 - b), at least one of them will have obtained all wins needed within 19 - a - b games. For instance, if we start from a + b total wins so far, adding (19 - a - b) more wins leads to a grand total of (a + b) + (19 - a - b) = 19. Because either Fermat or Pascal will have 10 out of those 19, the game cannot remain undecided after that many trials.

• A subtle pitfall is not recognizing that the “game is forced to conclude by the time 19 total wins have been distributed between the two players.” The 19th overall win must push either Fermat or Pascal to the 10-win mark.

How do we generalize this to a best-of-N format where N is not necessarily 19?

Many competitions use a best-of-N format (e.g., best-of-7, best-of-11). The number 19 arises from the specific scenario where each needs 10 total wins. In general, if the match is first-to-K wins, the total maximum number of games is 2K - 1.

Answer Explanation:

• For a general best-of-(2K - 1) match, if we interrupt at (a, b), the maximum number of additional games that could be needed is (K - a) + (K - b) - 1 = 2K - (a + b) - 1.

• The probability that a certain player eventually wins is then the sum of binomial probabilities that the player wins enough future games to reach K before the other.

• The key formula for the probability that the player with a current wins eventually reaches K first remains:

• provided each game is still a fair 1/2 chance.

• A pitfall arises when K is very large. Summing binomial coefficients over a large number of terms could be computationally intensive, so one may resort to cumulative distribution function computations or approximation methods (e.g., normal approximation to the binomial) when K is large.

In practical implementations, how might floating-point issues or large values of binomial coefficients lead to numerical instability?

When summing binomial probabilities for large N, the individual terms could become very small or very large, leading to floating-point inaccuracies.

Answer Explanation:

• Binomial coefficients like C(N, k) can be enormous, even though the final probability might be within [0,1]. Directly computing these coefficients and then multiplying by (1/2)^N could cause underflow or overflow if N is large.

• Standard libraries often implement binomial probabilities via logarithms to maintain numerical stability. For instance, one might compute log(C(N, k)) = ln(Gamma(N+1)) - ln(Gamma(k+1)) - ln(Gamma(N-k+1)) and similarly add log probabilities, then exponentiate at the end.

• A pitfall is using naive multiplication in a loop, which might cause the probability to become 0 or Infinity in floating-point representation. Hence, stable algorithms or well-tested library functions are essential in real-world data science applications.

Could we solve the problem using a dynamic programming (DP) approach rather than summing binomial distributions?

Sometimes, an interviewer might ask if there is a more incremental method to compute the probability of eventually reaching 10 wins.

Answer Explanation:

• One can model the problem as a Markov chain, where the state is (x, y) representing how many wins each player has. Transitions occur with probability 1/2 from (x, y) to (x+1, y) or (x, y+1).

• The DP solution might look like this (in pseudo-code):

  1. Create a 2D table DP[x][y] for x=0..10, y=0..10.

  2. DP[10][y] = 1 for all y < 10, because if Fermat is at 10, he has already won.

  3. DP[x][10] = 0 for all x < 10, because if Pascal is at 10, Fermat can no longer win.

  4. For each x, y in descending order, DP[x][y] = (1/2)*DP[x+1][y] + (1/2)*DP[x][y+1].

• DP[a][b] directly gives the probability that Fermat eventually wins if the current state is (a, b).

• The pitfall is that while DP and the binomial-sum approach are consistent, implementing DP might be more intuitive for some but less direct than a closed-form binomial summation. In large K scenarios, 2D DP might also become big, but it remains feasible for up to around K=1000 or so.

How do we handle a scenario where games can end in a draw, and the match continues until one player has 10 wins?

Real-world variations might allow for a draw in a single game (rare in typical board games, but can happen in certain sports).

Answer Explanation:

• If there is a probability d for a draw, then the probability Fermat wins is p, and Pascal’s probability of winning is q, with p + q + d = 1. The game only advances a player’s score if either Fermat or Pascal wins; a draw means replaying a new game.

• One approach is to note that the probability the match produces a winner in any given trial is p + q = 1 - d. The chance that Fermat is the eventual winner of a “decisive” game is p/(p+q).

• Mathematically, each game is effectively a “Bernoulli trial” of success probability p/(p+q), but you have geometric “repetitions” with success = “someone wins.” We can treat the draws as repeated attempts that do not alter the state (a,b).

• The pitfall is ignoring the infinite geometric series of potential repeated draws. You can factor out (1-d)^n or apply an infinite sum that accounts for the probability of a decisive outcome eventually emerging. Typically, you can reduce it to the same binomial framework but with p replaced by p/(p+q).

Could we incorporate Bayesian updates if we do not know the probability of a Fermat win, but estimate it from observed data?

In practical data science, we might not know the true probability that Fermat wins each game, especially if the players’ skill levels are unknown.

Answer Explanation:

• We can treat p as a random variable with a prior distribution (e.g., Beta(α, β)). As we observe each game, we update α, β based on the outcome. For instance, if we see a Fermat win, α becomes α+1. If Pascal wins, β becomes β+1.

• Once the match is interrupted at (a, b), we can integrate over the posterior distribution of p to estimate the probability that Fermat reaches 10 first. This leads to a hierarchical approach:

  1. Posterior for p given the existing data (a, b) (and any additional data about how a and b were reached).

  2. Then compute the probability of eventually reaching 10 wins by integrating the binomial expression over the posterior of p.

• The pitfall here is complexity: the integral might require numerical methods. However, the Beta-Binomial model is a conjugate pair, which can sometimes simplify the math. For large data, one typically relies on approximations or sampling.