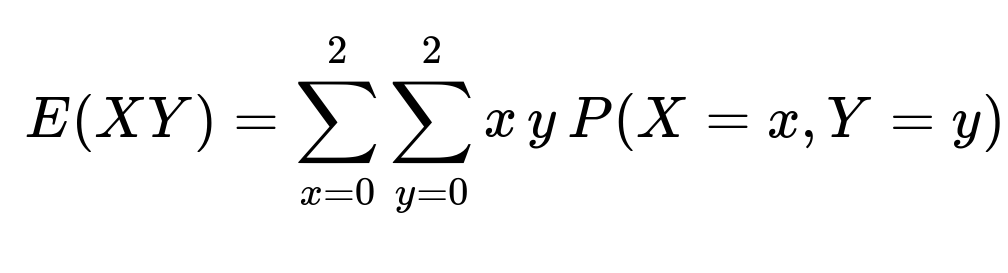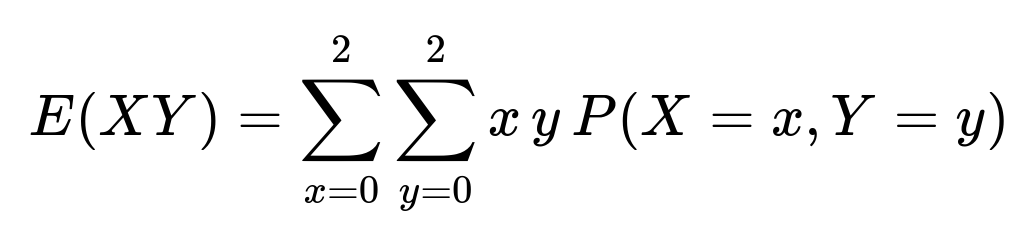ML Interview Q Series: Calculating E(XY) from Joint PMF for Overlapping Coin Toss Heads
Browse all the Probability Interview Questions here.
A fair coin is tossed three times. Let X be the number of heads among the first two tosses and Y be the number of heads among the last two tosses. What is the joint probability mass function of X and Y? What is E(XY)?
Short Compact solution
The joint probability mass function is:
P(X=0, Y=0) = 1/8
P(X=0, Y=1) = 1/8
P(X=1, Y=0) = 1/8
P(X=1, Y=1) = 1/4
P(X=1, Y=2) = 1/8
P(X=2, Y=1) = 1/8
P(X=2, Y=2) = 1/8
From this distribution, we use the formula for the expectation of a product:
Substituting the probabilities: 1 * 1/4 + 2 * 1/8 + 2 * 1/8 + 4 * 1/8 = 1.25
Thus, E(XY) = 1.25.
Comprehensive Explanation
How X and Y are defined
We have three independent tosses of a fair coin:
Let X = number of heads in the first 2 tosses.
Let Y = number of heads in the last 2 tosses.
X can take values 0, 1, or 2. Y can also take values 0, 1, or 2. Because each coin toss is fair and all three tosses are independent, each of the 2^3 = 8 possible outcomes has probability 1/8.
Enumerating all outcomes
To see exactly why the listed probabilities hold, we can enumerate every outcome and record the values of X and Y:
TTT => first two: TT => X=0; last two: TT => Y=0
TTH => first two: TT => X=0; last two: TH => Y=1
THT => first two: TH => X=1; last two: HT => Y=1
THH => first two: TH => X=1; last two: HH => Y=2
HTT => first two: HT => X=1; last two: TT => Y=0
HTH => first two: HT => X=1; last two: TH => Y=1
HHT => first two: HH => X=2; last two: HT => Y=1
HHH => first two: HH => X=2; last two: HH => Y=2
Counting how many times each (X, Y) pair appears among these 8 outcomes gives us the joint pmf. Since each outcome is equally likely (1/8):
(X=0, Y=0) appears 1 time => 1/8
(X=0, Y=1) appears 1 time => 1/8
(X=1, Y=0) appears 1 time => 1/8
(X=1, Y=1) appears 2 times => 2/8 = 1/4
(X=1, Y=2) appears 1 time => 1/8
(X=2, Y=1) appears 1 time => 1/8
(X=2, Y=2) appears 1 time => 1/8
Computing E(XY)
To find E(XY), we sum over all possible (x, y) pairs:
Breaking it down:
For (X=1, Y=1): 1 * 1 * 1/4 = 1/4
For (X=1, Y=2): 1 * 2 * 1/8 = 2/8 = 1/4
For (X=2, Y=1): 2 * 1 * 1/8 = 2/8 = 1/4
For (X=2, Y=2): 2 * 2 * 1/8 = 4/8 = 1/2
Adding them up: 1/4 + 1/4 + 1/4 + 1/2 = 1.25
Hence, E(XY) = 1.25.
Are X and Y independent?
No, X and Y are not independent. Intuitively, the second toss affects both X and Y. Specifically, X depends on whether the second toss is a head, and Y also depends on whether the second toss is a head. This creates a dependency.
A quick check of independence would be to see if P(X=1, Y=1) equals P(X=1)*P(Y=1).
P(X=1) = Probability of exactly 1 head in first 2 tosses. That occurs if we have (H, T) or (T, H), so 2 out of 4 possibilities => 1/2.
P(Y=1) = Probability of exactly 1 head in last 2 tosses => also 1/2 by symmetry.
Thus P(X=1)*P(Y=1) = 1/2 * 1/2 = 1/4.
But we see P(X=1, Y=1) = 1/4 from the joint distribution. That part looks consistent, but you have to check the entire distribution (for instance, P(X=2, Y=2) does not factor nicely to P(X=2)*P(Y=2) ), so they are indeed dependent once you examine the full range of events.
What is Cov(X, Y)?
The covariance can be computed as E(XY) - E(X)E(Y). We know E(XY) = 1.25.
E(X) is the expected number of heads in the first 2 tosses => 2 tosses each with probability 0.5 => E(X) = 1.
E(Y) is the expected number of heads in the last 2 tosses => also 1.
So E(X)E(Y) = 1 * 1 = 1. Thus Cov(X, Y) = 1.25 - 1 = 0.25.
Correlation between X and Y
Correlation = Cov(X, Y) / (sqrt(Var(X)) sqrt(Var(Y))).
Var(X) for the number of heads in 2 fair coin tosses is 2 * 0.5 * 0.5 = 0.5.
Var(Y) is similarly 0.5.
Hence Corr(X, Y) = 0.25 / (sqrt(0.5)*sqrt(0.5)) = 0.25 / 0.5 = 0.5.
This indicates a moderate positive correlation between X and Y.
Could we reason about E(XY) in a more direct combinatorial way?
Yes. Another method to find E(XY) is to define indicator variables:
Let X = I(X_1) + I(X_2), where I(X_i) is 1 if the i-th toss is heads, 0 otherwise.
Let Y = I(X_2) + I(X_3). Then XY = (I(X_1) + I(X_2)) (I(X_2) + I(X_3)).
Expanding: XY = I(X_1)I(X_2) + I(X_1)I(X_3) + I(X_2)^2 + I(X_2)I(X_3).
But I(X_2)^2 = I(X_2), because it is an indicator variable. Taking expectations and using linearity: E(XY) = E(I(X_1)I(X_2)) + E(I(X_1)I(X_3)) + E(I(X_2)) + E(I(X_2)I(X_3)).
Then we evaluate each term carefully using the fact that coin tosses are fair and (except for the second toss common to X and Y) are independent. You end up getting the same 1.25 value. This approach is common in advanced probability settings and is often used to confirm the result or to derive Cov(X, Y) more systematically.
Implementation Example in Python
import itertools
# All possible outcomes of 3 coin tosses
# 'H' for heads, 'T' for tails
outcomes = list(itertools.product(['H','T'], repeat=3))
# Compute X and Y
def num_heads(seq):
return sum(s == 'H' for s in seq)
pmf = {}
for outcome in outcomes:
# first 2 tosses
X_val = num_heads(outcome[:2])
# last 2 tosses
Y_val = num_heads(outcome[1:])
pmf[(X_val, Y_val)] = pmf.get((X_val, Y_val), 0) + 1/8 # each outcome has prob=1/8
E_XY = 0
for (x, y), prob in pmf.items():
E_XY += x * y * prob
print("Joint PMF:", pmf)
print("E(XY):", E_XY)
This code enumerates all outcomes, calculates X and Y for each outcome, aggregates the joint distribution (X, Y), and finally sums up xyprob to get E(XY).
By running this code, you will see that E(XY) = 1.25.
Below are additional follow-up questions
Could we approach this problem using probability generating functions?
Yes. While enumerating outcomes directly is straightforward for three tosses, probability generating functions (PGFs) offer a systematic approach for more complex scenarios. Here, one could construct a bivariate generating function G(s, t) that tracks the distribution of heads across the positions relevant to X and Y:
Let H1, H2, H3 be the indicator random variables for heads on tosses 1, 2, and 3, respectively (each 1 if heads, 0 if tails).
We want X = H1 + H2 and Y = H2 + H3. Consider the polynomial in two variables s and t that corresponds to each possible realization of (H1, H2, H3):
For each outcome (h1, h2, h3), where h1, h2, h3 are 0 or 1, we include a term (s^(h1+h2)) (t^(h2+h3)) with the appropriate probability factor.
Because each of the 8 outcomes is equally likely (probability 1/8 if the coin is fair), G(s, t) becomes a sum of terms of the form (1/8)*s^(x) t^(y). You can then read off the coefficient of s^x t^y to get P(X=x, Y=y).
A key subtlety: If the coin or number of tosses grows, the direct enumeration becomes cumbersome, but a generating-function approach can systematically capture the overlaps (like H2 belonging to both X and Y). In actual practice, for large numbers of tosses or complicated overlaps, you would rely on algebraic manipulations of PGFs rather than enumerating every possibility.
Pitfall to watch out for:
In multi-variable generating functions, it is easy to mix up exponents or lose track of which toss contributes to which variable. Carefully define the exponents to represent each random variable’s count.
How would we generalize E(XY) if the coin is biased?
When the coin has probability p of landing heads (instead of 0.5), the joint pmf changes because each outcome is no longer simply 1/8. Instead, an outcome with k heads among the three tosses has probability p^k (1-p)^(3-k). X and Y remain the counts in the first two and last two tosses, respectively, but each (x, y) combination must be re-weighted accordingly.
A common approach:
Enumerate all eight outcomes (H/T patterns).
For each outcome with, say, h1 = 1 if toss 1 is heads, and 0 otherwise, compute probability p^(h1 + h2 + h3) (1-p)^(3-(h1 + h2 + h3)).
Aggregate probabilities by (X, Y).
Multiply x*y times that probability, and sum over all x, y.
Alternatively, you can use indicator variables:
X = H1 + H2
Y = H2 + H3
Then XY = (H1 + H2)(H2 + H3). By expanding and taking expectation term by term, you incorporate P(H2=1) = p and so on. This avoids enumerating all outcomes if you track each pairwise correlation carefully.
Potential pitfalls:
Forgetting to adjust for the correlation introduced by H2 being common to both X and Y.
Mixing up the probability p for heads with the assumption p=0.5 from the fair coin scenario.
What if we consider X = number of tails in the first two tosses instead of heads?
Then X can still be 0, 1, or 2, but now it represents tails in tosses 1 and 2. Meanwhile, Y is the number of heads in tosses 2 and 3. The counting changes:
X = 2 - (number of heads in tosses 1 and 2).
Y = (number of heads in tosses 2 and 3).
You can still enumerate all 2^3 = 8 outcomes. The difference is that for a given outcome (e.g., THT), X is 1 if tosses 1 and 2 have exactly 1 tail, while Y might be 1 for one head in tosses 2 and 3, and so on. The joint pmf structure remains valid, but you need to re-compute which outcomes map to which (x, y). This is a good exercise to test whether you fully grasp how to define random variables on overlapping or partially overlapping coin tosses.
Edge case to watch out for:
If you try to rely on symmetry arguments from the original definition of X and Y, note that switching from heads to tails in one variable can break an otherwise symmetrical pattern. You may have to do a fresh enumeration.
How do we extend the idea of overlap if we had 4 coin tosses and define X as heads in tosses 1,2 and Y as heads in tosses 2,3,4?
In that case, X = H1 + H2, and Y = H2 + H3 + H4. Now Y depends on three tosses while X depends on only two, but they still overlap on toss 2. The principle is the same:
List out all 16 outcomes, or use indicator variables.
X = H1 + H2, Y = H2 + H3 + H4.
Overlap is in H2, so you will see correlation.
E(XY) can be computed by summing xyP(x, y) or by expanding X*Y in terms of H1, H2, H3, H4.
A subtlety arises because Y is “longer” (it has 3 tosses contributing). This can increase E(XY) beyond what you might guess from a smaller overlap. Common pitfall:
Overlooking the fact that H3 and H4 only appear in Y, not in X, which changes their correlation structure.
Is E(X+Y) always equal to E(X) + E(Y) even when X and Y are not independent?
Yes, the linearity of expectation states that E(X+Y) = E(X) + E(Y) regardless of whether X and Y are independent. In our original 3-toss example, we can show:
E(X) = 1, E(Y) = 1
E(X+Y) = 2
Even though X and Y are correlated, linearity of expectation still holds. A common mistake is to think that lack of independence might prevent the sum of expectations from being simply additive. But expectation is additive regardless of dependence.
If we define Z = 1 when X = Y and 0 otherwise, how do we compute P(X=Y)?
In the original 3-toss setup (fair coin):
We look for outcomes where the number of heads in the first two tosses equals the number of heads in the last two tosses.
The pairs (X, Y) that match are (0, 0), (1, 1), (2, 2). You can add up probabilities for those three events:
P(X=0, Y=0) = 1/8
P(X=1, Y=1) = 1/4
P(X=2, Y=2) = 1/8
Summation = 1/8 + 1/4 + 1/8 = 1/2
Hence P(X=Y) = 1/2. This means half the time, you’ll see the same number of heads in the first two and the last two tosses. Pitfall:
Confusing X=Y with X+Y = some constant. They’re different events. X=Y is about equality, not about summation.
How would we check for higher-order moments, like E(X^2 Y) or E(X Y^2)?
For higher-order moments, you must sum over all x^2 * y (or x * y^2) times the joint probability P(X=x, Y=y). Alternatively, you can expand in terms of the indicator variables for each toss. For example, to compute E(X^2 Y):
Write X = H1 + H2, Y = H2 + H3.
Then X^2 = (H1 + H2)^2 = H1^2 + 2H1H2 + H2^2 = H1 + 2H1H2 + H2 (since H1^2 = H1 for an indicator).
So X^2 Y = (H1 + 2H1H2 + H2)(H2 + H3). Expand out each term and compute expectation by noting independence of H1, H3 from each other, partial dependence on H2, etc.
This process becomes more tedious for large numbers of overlaps or for biased coins, but it systematically yields the correct results. Pitfall:
Easy to miscount terms like H2^2, which should revert to H2 for an indicator variable.
Overlooking that H2 appears in multiple terms can lead to double counting.
Can we use simulation to verify E(XY) or other quantities quickly?
Absolutely. A quick Monte Carlo simulation approach is:
Simulate many trials of 3 coin tosses.
In each trial, compute X and Y.
Average the product X*Y across all trials.
For a large number of simulations, the empirical mean of X*Y should approximate the true E(XY). This is often helpful if you suspect an arithmetic mistake or if you want to generalize to complicated scenarios (e.g., 10 tosses, overlapping windows) where a closed-form solution is still possible but might be tedious.
Edge cases:
In practice, if the coin’s bias p is unknown, your sample simulation must reflect that uncertain distribution. If p changes in real time, you need adaptive approaches or time-varying probabilities.
Simulations can produce approximate values quickly, but you must ensure you run a sufficiently large number of iterations and account for random variation.
What if we required a minimum total number of heads across all three tosses before defining X or Y?
A scenario might be: “Let W = total number of heads among the three tosses. We only define (X, Y) if W >= 1, otherwise disregard them.” This modifies the sample space and effectively conditions on W >= 1. The probabilities then need to be rescaled:
Restrict to outcomes where the total heads is at least 1, ignoring the event TTT.
Recompute P(X=x, Y=y | W >= 1).
Then calculate E(XY | W >= 1).
Pitfalls:
Failing to realize that TTT is excluded from the sample space, so you must divide each probability by 1 - 1/8 = 7/8 in the fair coin case.
Overlapping definitions remain, so you still have to consider the role of the second toss in both X and Y.
This conditional approach is essential if, for instance, you say “We only analyze X and Y if we know at least one head was tossed.”