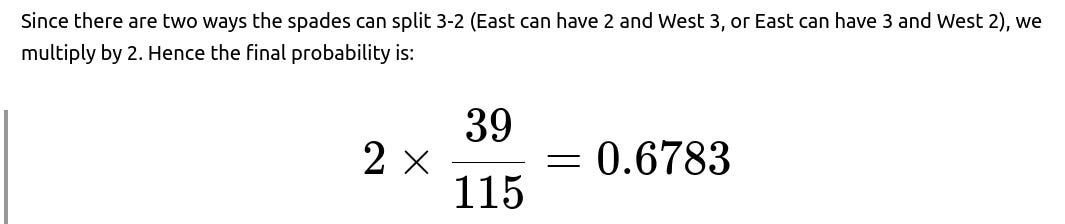ML Interview Q Series: Calculating Bridge Spade Split Probability Using Combinations
Browse all the Probability Interview Questions here.
Question: Suppose you know that the hands of you and your bridge partner contain 8 of the 13 spades in the deck. What is the probability of a 3-2 split of the remaining 5 spades in the bridge hands of your opponents?
Short Compact solution
Call your opponents East and West. First compute the probability that East has 2 spades and West has 3 spades. We count the ways to choose 2 spades out of the 5 unaccounted spades and 10 other suits out of the 21 available, and divide by the total ways to choose any 13 cards for East out of the 26 remaining cards in the deck. This is:
Comprehensive Explanation
The key idea is to recognize that once you and your partner collectively hold 8 of the 13 spades, only 5 spades remain in the deck. Your two opponents (East and West) share the remaining 26 cards of which 5 are spades and 21 are other suits.
In bridge, each opponent’s hand consists of 13 cards. We want to find the probability that these 5 spades are split between East and West in a 3-2 configuration (it could be East having 3 while West has 2, or vice versa).
To calculate the probability that East has exactly 2 of the 5 spades, we note that East must then have 11 other suits (because East’s hand is 13 cards total). Thus, the number of ways for East to have exactly 2 spades out of 5 is choose(5,2). The remaining 11 cards of East’s hand must come from the 21 non-spade cards, and there are choose(21,11) ways for that. (Equivalently, one might see choose(21,10) if using complementary counting, but it matches numerically because choose(21,10) = choose(21,11).)
The total ways to form East’s 13-card hand from the 26 unknown cards is choose(26,13). Dividing the favorable ways by the total ways gives the probability that East receives exactly 2 spades (and therefore West has exactly 3 spades). Because there is also the symmetrical possibility that East has 3 spades and West has 2, we multiply this probability by 2 to obtain the final answer.
Conceptually, this is a direct application of the hypergeometric distribution. The hypergeometric distribution describes the probability of k “successes” (in this case, spades) in n draws (East’s 13 cards) without replacement from a finite population (the 26 unknown cards) containing a certain number of successes (5 spades).
Potential Follow-Up Question: Why is the total number of ways for the opponents’ combined hands not explicitly considered in the calculation?
Because we only need to consider the ways that East’s specific 13 cards can be formed from the 26 unknown cards. Once East’s cards are fixed, West’s cards are determined from the leftover 13 cards automatically. Thus, it suffices to compare the favorable ways East’s hand can be formed (with a specific number of spades) to the total ways East’s 13 cards can be formed. We do not have to enumerate West’s hand separately, as that would be double-counting the same scenario in a more complicated manner.
Potential Follow-Up Question: How does this relate to the hypergeometric distribution in machine learning or data science contexts?
The hypergeometric distribution appears whenever there is sampling without replacement from a finite population that contains a certain number of “success states.” In data science, for example, this might appear in evaluating the probability of drawing certain categories from a dataset partitioned into different labels or classes without replacement. The same formula applies: Probability(k successes in n draws) = [choose(K, k)*choose(N-K, n-k)] / choose(N, n), where:
N is the total population size.
K is the total number of success states in the population.
n is the number of draws.
k is the number of successes among the drawn items.
Here, N = 26 (opponents’ total unknown cards), K = 5 (remaining spades), n = 13 (cards for East), and k = 2 (the spades East gets). The result is precisely the fraction that forms the basis of our 3-2 split probability.
Potential Follow-Up Question: Could we also directly sum the probabilities for East having 2 spades and East having 3 spades without multiplying by 2?
Yes, you can do that explicitly:
Probability(East has 2 spades) = choose(5,2)*choose(21,11) / choose(26,13)
Probability(East has 3 spades) = choose(5,3)*choose(21,10) / choose(26,13)
It turns out that choose(5,2)*choose(21,11) = choose(5,3)*choose(21,10), so each term is 39/115. Adding them yields 2 * 39/115 = 78/115, which is about 0.6783.
Potential Follow-Up Question: What are some edge cases or subtle points to watch out for in more general card-splitting problems?
One subtlety is ensuring that you correctly account for how many cards are “known” and how many are “unknown.” For instance, if some cards are visible (e.g., in a real card game scenario, certain spades might have been played or exposed), you must adjust the total population of unknown cards and the number of unknown spades accordingly.
Another issue is whether the decks or partial decks are being reshuffled at any point (in real bridging or real gaming, they are typically not), which would invalidate the straightforward hypergeometric approach. Always confirm that sampling is done without replacement for these classic probability approaches to be valid.
Below are additional follow-up questions
What if the deck is incomplete or damaged, causing an unknown number of spades to be missing?
One subtle real-world complication is that sometimes a deck may not have exactly 52 cards. For instance, a card might be lost or damaged. If a spade is missing (and you do not realize it initially), your assumption that there are 13 total spades will be violated. This leads to an entirely different probability model because:
You no longer know with certainty how many total spades remain.
You cannot rely on the standard combinatorial counts (choose(26,13), etc.).
In practice, if you discovered that a card was missing, you would have to adjust your calculation by re-estimating how many spades remain in the unknown portion of the deck. Any probability you computed under the assumption of a full deck could be invalid. The pitfall is assuming a standard scenario when some physical constraint (like a missing card) undermines that assumption.
How does the probability change if the deck has been tampered with and is not uniformly shuffled?
In standard probability questions, we assume all deals are equally likely. However, if the deck is tampered with—say, certain suits are more likely to cluster together or the shuffling is biased—the uniform assumption breaks down. This means:
The straightforward combinatorial calculations (choose(26,13) and so on) no longer apply.
You would need to model or estimate the actual distribution or “shuffling process” that generated the hands.
For example, if someone arranges the deck such that spades tend to come in consecutive blocks, the chance of a particular 3-2 split can differ significantly from the hypergeometric result. The pitfall here is not questioning the assumption of uniform randomness in real settings, especially when the deck shuffle might be suspicious.
Could we approach this from a Bayesian perspective if new information arrives mid-game?
Yes. In Bayesian terms, the calculation we did is the prior probability: the chance of a 3-2 split given no extra evidence apart from the known distribution of spades in your and your partner’s hands. If, during the play of the hand, you see certain cards revealed, or an opponent makes certain bids or plays that suggest a spade distribution, you then update your probability distribution.
For instance, if an opponent shows out of spades earlier than expected, or if certain discards or signals in the bidding phase give clues about spade holding, you incorporate that evidence to refine your estimate. The challenge (and pitfall) is properly updating the probability rather than continuing to rely on the original calculation. In real bridge play, good players are constantly updating these probabilities based on partial information revealed at the table.
Can we generalize this to probabilities of other suit splits, such as a 4-1 or 5-0 split?
Absolutely. The same combinatorial logic applies. For instance, if you want the probability that East holds exactly 4 spades (and thus West has 1), you replace the “2” in choose(5,2) with “4,” and reduce the “21 choose 10” to match the correct number of non-spade cards (East would now have 9 non-spade cards). More generally:
Probability(East has k spades) = choose(5, k) * choose(21, 13 - k) / choose(26, 13).
From that, you can figure out the complementary distribution for West’s hand. A common pitfall is failing to track how many cards remain for the other suits. You must always confirm that the total count of cards in each hand remains 13.
How can we interpret this probability in the context of making in-game decisions in bridge?
Knowing the probability of a 3-2 split (or any particular suit distribution) is crucial when deciding how to play a suit or when planning a line of play. For example, if the probability of a 3-2 split is significantly higher than that of a 4-1 or 5-0 split, many standard bridge strategies (like finesses or ruffing lines) rely on playing for the most likely distribution. The pitfall for newer players is ignoring these probabilities and assuming best-case scenarios or improbable distributions.
What if your partner’s bidding suggests that your partner actually has more or fewer spades than initially counted?
Sometimes the bidding phase of bridge provides strong evidence about how many spades partner (or the opponents) hold. For example, if your partner opens or overcalls with spades, they may well have at least 5 spades. Conversely, they might have shown a short suit. If this conflicts with your initial count of 8 spades in your combined hands, you might have miscounted, or your partner could have an unusually long or short holding. You would need to:
Reassess the total spade distribution.
Potentially adjust the probability that the remaining spades are split 3-2 among the opponents.
A pitfall here is relying on the simplistic 8-spade assumption in the face of contradictory bidding clues. Real bridge decisions often integrate both combinatorial probabilities and inferences from the auction.
Does a combinatorial identity confirm that all possible splits of the 5 unknown spades add up to 1?
Yes. If you sum over all valid ways that East can hold k spades (k = 0, 1, 2, 3, 4, 5), you will cover every possible spade distribution for East and West. Each term would look like choose(5, k)*choose(21, 13-k) / choose(26, 13). Summing from k=0 to k=5 yields 1 (since exactly one of these must happen). A common pitfall is to forget a possible split (like 0-5 or 5-0) and end up with probabilities that do not sum to 1.
How might we use permutations instead of combinations, and what pitfalls might arise?
One could theoretically count permutations of cards (ways to order them) and then divide by the total orderings. However, since bridge deals do not depend on order—only on which 13 cards end up in a particular hand—using permutations can be prone to errors if not carefully accounted for. You would have to ensure that each of the 13 cards for East is considered in a distinct set of permutations and that you divide out the ordering that does not matter. The pitfall is overcounting if one fails to divide by the number of ways to permute the chosen 13 cards in East’s hand and similarly for West’s hand.
Does the standard dealing process in bridge always produce a perfectly uniform distribution?
By theoretical design, a well-shuffled 52-card deck is assumed to give an equally likely chance for any combination of 13 cards in a hand. However, many real-world shuffles can be imperfect. For instance, human shuffling methods may not randomize thoroughly, especially if done only a few times or if certain “riffle” patterns are repeated. This can skew the distribution. The pitfall is assuming perfect randomness in a practical scenario where shuffling might be suboptimal, leading to an unrealistic probability assessment.
How could knowledge of certain played cards during the play phase alter the probability of a 3-2 split?
During actual gameplay, some cards—spades or otherwise—become visible as they are played (or sometimes even revealed through claiming or misdeals). Once you see that specific spades are out of a particular opponent’s hand, that knowledge changes the distribution of unknown spades. You would effectively reduce the unknown population and reduce the count of unknown spades accordingly. If you discovered that East has already shown two spades in the play, and West has shown none, and there are three spades still unaccounted for, your probability of certain splits must be recalculated with this new evidence. The pitfall is failing to update the model after each piece of revealed information, which leads to using outdated probabilities in your strategic decisions.