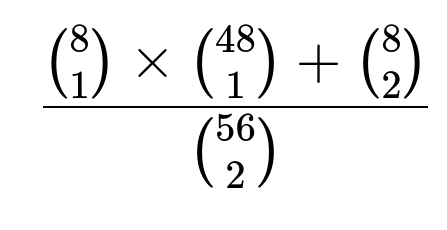ML Interview Q Series: Calculating Apartment Top-Floor Vacancy Odds Using Combinatorics
Browse all the Probability Interview Questions here.
Imagine a building with 7 floors and 8 apartments on each floor, making a total of 56 apartments labeled from 1 up to 56. A person is searching for a top-floor apartment (i.e., on the 7th floor, which contains 8 apartments). She learns that exactly two apartments in the building are vacant. What is the probability that at least one of these vacant apartments is on the top floor?
Short Compact solution
The sample space has all possible ways of choosing 2 vacant apartments out of 56. That gives a total of (56 choose 2) = 1540 equally likely outcomes. The number of outcomes where exactly one of the vacant apartments is on the top floor is (8 choose 1) * (48 choose 1) = 384. The number of outcomes where both vacant apartments are on the top floor is (8 choose 2) = 28. Summing these gives 412 favorable outcomes. Dividing by 1540 yields 412/1540 = 0.2675. Hence, the probability that there is at least one vacancy on the top floor is approximately 0.2675.
Comprehensive Explanation
The problem involves a building with 7 floors, 8 apartments per floor, for a total of 56 apartments. A person learns there are exactly two vacant apartments scattered somewhere in the building. She wants to know how likely it is that at least one of these vacant units is on the top floor.
Key Ideas
One way to solve the problem is to consider all possible ways of choosing 2 distinct apartments from the 56 total apartments. Each such pair is equally likely to be the vacant units.
In text form, the size of the sample space is choose(56,2). Each element in this sample space is a distinct pair of vacant apartments.
There are 8 apartments on the top floor (the 7th floor). We are interested in the event that at least one of the two vacant apartments is among these top 8.
Counting Favorable Outcomes
We can count the favorable outcomes by splitting into two mutually exclusive scenarios:
Exactly one of the vacant apartments is on the top floor.
Both vacant apartments are on the top floor.
The number of ways to pick exactly one vacant apartment on the top floor and the other somewhere else is choose(8,1) * choose(48,1). The first factor counts how to choose 1 apartment from the 8 on the top floor; the second factor counts how to choose 1 apartment from the remaining 48 on the lower floors.
The number of ways to pick both vacant apartments from the top floor is choose(8,2).
Hence, the total number of favorable outcomes is 384 + 28 = 412.
Final Probability Calculation
We place this result over the total number of ways to pick 2 apartments out of 56:
All terms in this expression count distinct pairs of apartments. Evaluating:
binom(56,2) = 1540
binom(8,1) * binom(48,1) = 384
binom(8,2) = 28
So the probability is (384 + 28) / 1540 = 412 / 1540, approximately 0.2675.
Alternative Approach Using Ordered Arrangements
Another perspective is to imagine listing all 56 apartments in some order. The first two positions in that list represent which apartments are vacant. One can then count how many permutations correspond to the case where neither of the first two positions is occupied by a top-floor apartment, and then subtract from 1. Doing so leads to the same probability of around 0.2675 that there is at least one vacant apartment on the top floor.
Follow-up question 1
Why do we consider choose(56,2) as the total sample space instead of, for example, permutations of vacant apartments?
When there is no inherent ordering or labeling of the pair of vacant apartments (i.e., it does not matter which one we “call” the first or second vacancy), each unordered pair of distinct apartments is a single equally likely outcome. Consequently, the correct count of total possible outcomes for picking 2 vacant apartments is choose(56,2). While one can use ordered permutations, that approach must be treated carefully so as not to overcount, and the final result would be the same once you account for all permutations consistently.
Follow-up question 2
Could we have found the probability by instead calculating the probability that there are no vacant apartments on the top floor?
Yes. Sometimes it is easier to compute the complement of the desired event. The probability that neither vacant apartment is on the top floor is the probability of choosing both vacant apartments from the 48 non–top-floor apartments. There are choose(48,2) = 1128 ways to choose 2 apartments from those 48. Since there are choose(56,2) = 1540 ways to choose 2 apartments from all 56, the probability that both vacant apartments are off the top floor is 1128 / 1540, which is approximately 0.7325. Therefore, the probability that at least one is on the top floor is 1 − 1128/1540 = 0.2675.
Follow-up question 3
Is there a direct real-world interpretation of these combinations and probabilities?
Yes. Each apartment is equally likely to be vacant. So for any two distinct apartments, the chance of that specific pair being the vacant one is 1 / choose(56,2). Hence, adding up all pairs that include at least one top-floor apartment and dividing by choose(56,2) naturally gives the required probability.
Follow-up question 4
How might correlations or dependencies between apartments affect the probability in a real setting?
In practice, vacancies might not always be independent or equally likely if certain floors are more popular, or if there are rent differences. In such a scenario, one might need a different probability model that accounts for these possible dependencies. However, for an idealized uniform-random scenario where each apartment has an equal chance of being vacant, the calculation above holds exactly.
Follow-up question 5
How does this approach generalize to more than two vacant apartments?
If there were, say, k vacant apartments, we would count the total number of ways to choose k apartments from 56, and then count in how many ways at least one of those k apartments is on the top floor. Often, it is easier to compute the complement: “None of the k vacant apartments is on the top floor,” which is choose(48,k) ways out of choose(56,k). The probability would then be 1 − [choose(48,k) / choose(56,k)], which is the probability that at least one of the k vacant apartments is on the top floor.
Below are additional follow-up questions
What if we want the probability that exactly one vacant apartment is on the top floor, rather than at least one?
To determine this, we would focus on the scenario where precisely one of the two vacant apartments lies on the top floor. We can derive it directly by counting the number of ways to choose 1 apartment out of the 8 on the top floor and 1 apartment out of the 48 on all other floors, i.e. choose(8,1)*choose(48,1). Then we divide by choose(56,2), the total ways of picking any 2 vacant apartments from 56. Concretely:
Numerator: choose(8,1)*choose(48,1) = 384
Denominator: choose(56,2) = 1540
Hence the probability is 384 / 1540 = 0.2494. This value highlights the difference between “at least one” and “exactly one.” In practical terms, it shows that if the building occupant is fine with having exactly one top-floor vacancy (perhaps for lesser crowding or other personal preferences), this figure clarifies the precise likelihood.
A common pitfall is mixing up “exactly one” with “at least one,” so carefully distinguishing these events helps prevent erroneous computations.
How would the probability change if there were different numbers of apartments on each floor?
If each floor did not have the same number of apartments, then the total number of apartments on the top floor might differ from 8. Let’s say the top floor now has T apartments, while the entire building has N total apartments. The probability of having at least one vacant apartment on the top floor still follows the same reasoning, but with updated counts:
Total ways to pick 2 vacant apartments from N total apartments = choose(N,2).
Ways to pick at least one apartment from the T top-floor apartments = choose(T,1)*choose(N−T,1) + choose(T,2).
Substituting the correct T and N in these combinatorial expressions gives the precise probability. A subtlety arises if floors below the top vary in apartment count. We must then track which floor is designated as “top” (T apartments) and how many total apartments N are in the building. The logic remains straightforward, but clarity in labeling floors is crucial to avoid confusion.
What if we only know that two specific floors—one of which is the top floor—have at least one vacancy, and we want the probability that the top floor is actually the one with both vacancies?
If it were known that exactly two floors have the vacant apartments, and one of those floors is the top floor, we want the probability that the top floor contains both. We have:
The “top floor” has T=8 apartments.
Suppose the other identified floor has M apartments.
We know that among these two floors alone, there are exactly 2 vacancies in total.
The chance that both vacancies are on the top floor translates to the probability of picking both from T apartments out of the combined T+M apartments. Here, we compute choose(T,2)/choose(T+M,2). This ratio represents the fraction of ways to pick 2 vacant apartments exclusively from the top floor, out of all ways to pick 2 vacant apartments from both floors combined.
A subtle pitfall is to remember that if we have prior knowledge that these two floors collectively contain both vacancies, we ignore all other floors in the probability space. Failing to condition on this knowledge would lead to an incorrect probability calculation.
What if the person heard that two vacant apartments exist but also learned that exactly one is on a “corner” unit (assuming some apartments are singled out as “corner” units)? How does that change the probability of having a vacancy on the top floor?
Once you incorporate the extra piece of information—one vacancy is known to be a corner apartment—the sample space narrows to all pairs of apartments where exactly one of them is from the set of corner units. Then you would ask: among that restricted set of pairs, how many have at least one on the top floor? The calculations might become more involved, as you must first identify how many corner apartments exist on each floor and how many are on the top floor. The essential steps are:
Count how many pairs contain exactly one corner unit.
Among these pairs, count how many also include a top-floor apartment (or specifically account for the top-floor corner and non-corner possibilities).
Divide the favorable count by the restricted sample space count.
A pitfall is trying to mix unconditional events with conditional ones. Once we know exactly one vacancy is a corner unit, we do not consider pairs where neither or both units are corners. This is a typical example of how additional constraints reduce the sample space and can significantly alter the probability.
How would you account for the possibility that vacancies might cluster, for instance if apartments next to each other are more likely to be vacant simultaneously (perhaps due to shared ownership or connected leases)?
Clustering or correlation means that the event of one apartment being vacant is not independent of others. Instead of each pair being equally likely, we have different probabilities for certain configurations. To model this, you would replace uniform combination counts with probabilities that reflect the correlation. In other words, if adjacency or some other factor raises the chance that apartments on the same floor end up vacant together, you would need:
A probability distribution P(i,j) specifying the likelihood that apartments i and j are simultaneously vacant.
Summation of P(i,j) over all i,j pairs that include top-floor apartments.
This demands more advanced statistical or probabilistic modeling (e.g., Markov random fields, copulas, or custom correlation structures). A key pitfall is continuing to use plain combinatorial counts without accounting for the fact that “some pairs are more probable than others.” Without the correct weighting for correlated events, your probability estimate would be inaccurate.
How would you adapt the formula if you only know the total number of vacancies but not exactly that it is two?
When you merely know the total number of vacancies in the building is an unknown random variable, you need the distribution for the number of vacant apartments. For example, if the number of vacancies follows some known distribution (like a Binomial with parameters n=56, p for probability of any unit being vacant), then you must sum over all possible numbers of vacancies, each weighted by its probability, and compute the chance that at least one is on the top floor. Concretely:
Let X be the random number of vacant apartments, with some distribution P(X=k).
Conditional on X=k, the probability that at least one vacancy is on the top floor is 1 − [choose(56−8,k)/choose(56,k)].
The overall probability is the expectation: ∑ [ P(X=k) * {1 − choose(48,k)/choose(56,k)} ] over all valid k.
The main pitfall is not properly integrating over the uncertainty in the total number of vacant units, which can lead to oversimplified or incorrect results.
What if the building has continuous changes in vacancy status, and you want the probability at a random snapshot in time?
Vacancies can change over time (people move in or out). If you only observe the building at a random time, the probability that the top floor has a vacancy might not match the simple combinatorial ratio if apartments have different turnover rates. You would then need a stochastic process model (e.g., a continuous-time Markov chain) describing how each apartment transitions between occupied and vacant. You would look at the stationary distribution or long-run fraction of time that each apartment is vacant, and then determine the probability that at least one top-floor apartment is vacant at a random moment. Pitfalls here include:
Ignoring the rates of transitions (some floors might have higher occupancy stability).
Failing to use the stationary or equilibrium probability when the process has run for a long period of time.
If apartments are subdivided or if multiple units on the top floor are “merged” into one large penthouse, does the combinatorial logic still work?
The combinatorial logic works exactly as long as each “apartment” is treated as a distinct entity with an equal chance of being vacant. But if one large penthouse merges several apartments, that aggregated space might be either vacant or not, effectively reducing the count of total distinct “vacancy possibilities.” For example, merging four top-floor apartments into a single large unit changes the building from 56 apartments to 53 apartments. Then:
The top floor might have fewer but larger units.
The number of ways to pick two vacant “units” is choose(53,2).
Subtleties arise if some floors are partially subdivided, leading to half-units or re-labeled apartments. The combinatorial approach remains valid only if each final labeled unit is considered separately with an equal chance of vacancy. Mixing labeled and unlabeled spaces or ignoring the re-labeled structure can yield incorrect results.