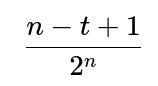ML Interview Q Series: Calculating Probability of Exact Consecutive Tails Block Using Combinatorics.
Browse all the Probability Interview Questions here.
Suppose you flip a fair coin 10 times. What is the probability that there are exactly three tails, all forming a single consecutive block? As an example, HHHTTTTHHH would satisfy this condition. Additionally, how can this be generalized for t consecutive tails in n flips (with t ≤ n)?
Comprehensive Explanation
To address the probability of having exactly three tails that appear consecutively in a sequence of ten fair coin flips, one can approach the problem using combinatorial reasoning. Since the coin is fair, each of the (2^{10}) possible outcomes (of 10 flips) is equally likely.
Core Idea for Three Consecutive Tails
The key observation is that if all three tails must be consecutive and no other tails appear outside that block, then we effectively place a single 'block' of three tails (TTT) somewhere among the 10 flips, with the remaining 7 flips being heads (H).
The number of ways to position a block of length 3 in a sequence of length 10 is 10 - 3 + 1 = 8. Specifically, that block could start at flip 1, flip 2, …, up to flip 8. Each valid sequence has the 3 consecutive tails plus 7 heads. Since the coin is fair, each sequence has probability 1 / 2^10.
Hence the probability of getting exactly three tails, all consecutive, is 8 / (2^10) = 8 / 1024 = 1 / 128.
Generalization for t Consecutive Tails in n Flips
When flipping a fair coin n times but insisting that exactly t ≤ n tails must appear, and they must all form one consecutive run:
The number of ways to place a single 'block' of t tails in a sequence of length n is n - t + 1. The rest n - t flips must be heads. Each unique sequence arises with probability 1 / 2^n for a fair coin.
Thus, the probability of obtaining exactly t consecutive tails (and no other tails) in n fair coin flips is:
where n is the total number of flips and t is the size of the consecutive tails block.
Below that formula:
n is the total number of coin flips.
t is the required consecutive tails count (t ≤ n).
(n - t + 1) is the count of ways to place that consecutive block of t tails among n flips.
1 / 2^n is the probability for any specific outcome of n fair coin flips.
Practical Perspective
This calculation is straightforward for a fair coin, but if the coin were biased (say probability p of landing tails and probability q = 1 - p of landing heads), the probability of exactly t consecutive tails (and no other tails) would become (n - t + 1) * p^t * q^(n - t), because you would place the single consecutive run of tails, which has probability p^t, and all the other flips (n - t of them) must be heads, each with probability q.
Common Follow-Up Questions
What if the coin is biased instead of fair?
If the coin has probability p of tails and q = 1 - p of heads, the probability of getting exactly t consecutive tails and no other tails is (n - t + 1) * p^t * q^(n - t). The reasoning is the same as in the fair coin case, except each tails flip now has probability p and each head flip has probability q.
What if the question asks for at least t consecutive tails?
Computing “at least t consecutive tails” is more complex because it involves counting all sequences that have a run of length t or more. Typically, one would use an inclusion-exclusion principle or a dynamic programming approach to count or calculate probabilities of sequences with runs of tails of length t or greater.
Is there a direct combinatorial formula for at-least-t consecutive tails?
One could rely on complementary counting: find the probability of no run of t tails (i.e., all runs of tails are strictly shorter than t), and subtract that from 1. That approach typically requires some form of dynamic programming or a combinatorial argument with recursion, because enumerating sequences that avoid a block of length t can get intricate for large n.
Could we simulate this probability for large n and t?
Yes, a Monte Carlo simulation can be used for large n, where we randomly generate many sequences of coin flips and estimate how often we observe exactly t consecutive tails or at least t consecutive tails. For instance:
import random
def simulate_consecutive_tails(n, t, trials=10_000_00):
count = 0
for _ in range(trials):
flips = [random.choice(['H','T']) for _ in range(n)]
# Count total number of tails
total_tails = flips.count('T')
if total_tails == t:
# Check if those t tails are consecutive
if 'T'*t in ''.join(flips):
# Ensure there are no extra tails outside the t block
# This can be done by verifying no other 'T' beyond the single block
if ''.join(flips).count('T') == t:
count += 1
return count / trials
prob_estimate = simulate_consecutive_tails(10, 3)
print(prob_estimate)
This code snippet (though not heavily optimized) shows how to empirically estimate the probability for exactly t consecutive tails in n flips. One might refine the string checking logic to ensure exactly one block of tails is present and no additional tails appear outside that block.
Edge Cases and Pitfalls
t = 0. This is the scenario of no tails at all; the probability for that (if the coin is fair) is 1 / 2^n.
t = n. This means all flips must be tails, so the probability is 1 / 2^n for fair coins.
Miscounting the number of ways to place the consecutive tails block if you do not carefully consider that you can place the t-block from position 1 to position n - t + 1.
Overlooking additional tails. The block must contain the total number of tails. If we say t = 3, we are ensuring there are no tails outside that block of 3.
These considerations help solidify understanding and ensure correct applications in real interview scenarios.
Below are additional follow-up questions
If we wanted the consecutive block of t tails to not occur at the very beginning or end of the sequence, how would we adjust the probability?
When the t tails must appear strictly within the interior of the n flips, we exclude the positions that place the t-block at the extreme ends. If the block cannot start at position 1, that removes 1 possible placement. Similarly, if the block cannot end at position n, that removes another placement. However, we must carefully consider overlap if t = n (which would make it impossible to place the block strictly inside) or if t is large enough that excluding the first and last positions double-counts the same restriction.
In general, if t < n, we have (n - t + 1) total placements for the block. Disallowing the first position eliminates 1, disallowing the last position eliminates 1 more, for (n - t + 1) - 2. However, if t = n, there are 0 placements that meet the stricter condition. Therefore, the final count of valid placements is (n - t - 1) so long as t < n.
Hence, for a fair coin, if 0 < t < n:
Number of valid positions = (n - t - 1).
Probability = (n - t - 1) / 2^n.
Pitfalls and Edge Cases:
If t = n, then the only way to get t tails is the entire sequence being tails, so it cannot be “inside,” hence probability = 0 for that stricter condition.
If t = n - 1, disallowing both ends might lead to 0 possible positions too (because you cannot start the block at position 2 and end at position n-1 if t = n - 1). Carefully check these boundary values.
Always confirm that (n - t - 1) is non-negative; otherwise, the count of valid placements becomes 0.
How can we find the expected position at which this t-tail block occurs, given it appears exactly once?
Once we have determined that exactly one block of t tails appears, each of the (n - t + 1) valid placements (in the fair-coin scenario) is equally likely among all the outcomes that satisfy the condition. The expected position of the leftmost tail in that block can be computed as the average of all possible starting positions, which are 1, 2, …, (n - t + 1).
The mean of these starting positions is [1 + 2 + … + (n - t + 1)] / (n - t + 1). Using the formula for the sum of the first k integers, the sum of 1 to k is k(k+1)/2. Here, k = (n - t + 1). So the expected starting position is: [(n - t + 1)(n - t + 2)] / [2(n - t + 1)] = (n - t + 2) / 2.
Pitfalls and Edge Cases:
This calculation presupposes that exactly one t-block is present (and no tails outside that block). If multiple such blocks are somehow allowed or if the coin is biased, adjustments are needed.
For a biased coin with probability p for tails, the placements are not equally likely among all outcomes that meet “exactly t consecutive tails” (though the count of valid placements is the same). The weighting of each placement is still uniform once you condition on the event that exactly one block of t tails appears, but you need to carefully verify that or recalculate the conditional probabilities.
What if we want to calculate the chance of exactly one block of t tails, but we also require a certain minimum number of heads in the sequence?
To incorporate a required minimum number of heads, say H_min, you must ensure that the rest of the flips (n - t in total) contain at least H_min heads. But since the scenario “exactly t tails” plus “they are all consecutive” already forces n - t heads in total, the condition “a certain minimum number of heads” becomes trivial as long as H_min <= n - t. If H_min > n - t, the probability is 0, because you do not have enough flips to reach that many heads while also fitting a block of t tails.
In summary:
If H_min <= n - t, no change to the original answer, because you already have n - t heads.
If H_min > n - t, probability is 0.
Subtlety arises if the question demanded “at least H_min heads that are not adjacent to the tails block.” That changes the counting because you might have to exclude heads that appear directly next to the t-block. You then must ensure additional spacing or further combinatorial constraints, which can be enumerated using block-and-gap style reasoning.
How does the reasoning change if the coin flips are part of a Markov chain, such that each flip depends on the previous outcome?
In a Markovian scenario, consecutive tails become more likely if a tail just occurred (or less likely, depending on transition probabilities). The flips are no longer independent Bernoulli trials.
One approach for a Markov chain with transition probabilities P(T|T) = a, P(H|T) = 1 - a, P(H|H) = b, P(T|H) = 1 - b, is to use dynamic programming. For instance, define a state representation that captures how many consecutive tails you currently have and how many flips remain. You recursively build the probability of eventually hitting exactly t consecutive tails (and no more tails beyond that block), but must carefully track whether the block is already complete or if you might exceed t.
Pitfalls and Edge Cases:
Overcounting sequences that contain more than one run of tails.
Properly handling the initial state, which might be unknown or might be given by a stationary distribution.
If you only want exactly one block of length t, ensure that if you surpass t consecutive tails, you move into a “failure” state, or if you break the run early, you move to a “no-run” state and continue.
What if we allow up to t tails in total, not necessarily exactly t, but still want any tails to be consecutive?
Allowing up to t tails, all consecutive, includes the scenarios of 0 tails, 1 tail, 2 tails, …, t tails, provided these tails form a single run if they occur.
You then sum over the probabilities of exactly k consecutive tails for k = 0 to t. For each k:
There are (n - k + 1) ways to place a k-length tails block.
Probability (for fair coin) is (n - k + 1) * (1 / 2^n).
Hence the probability of having a single run of tails whose length is anywhere from 0 up to t is:
Pitfalls and Edge Cases:
Make sure k = 0 is interpreted as no tails at all, which is 1 sequence out of 2^n.
Check boundary conditions for large t close to n (particularly t = n). In that case, you might be double counting or ignoring the requirement that it is a single run. In fact, k = n means the entire sequence is tails, which is indeed one valid sequence.
Could we extend the reasoning to multiple coins flipped in parallel or a 2D grid of coin flips where we want consecutive tails in rows or columns?
If the problem extends to a 2D grid (for instance, an n x m array of coin flips) and you want exactly t consecutive tails in a row or column (and none outside that block in that row/column), the counting becomes more intricate. You would:
Choose which row or column will contain the run of tails.
Place the run of length t in that selected row/column.
Ensure that all other positions in that row/column are heads.
Ensure that all other rows/columns contain zero tails.
In a fair coin 2D scenario, every cell is heads or tails with probability 1/2. The total number of possible grids is 2^(n*m). Counting the valid configurations requires careful enumeration, especially if you only want exactly one run of t tails in the entire grid and no other tails at all in the entire 2D array.
Pitfalls and Edge Cases:
It’s easy to overlook the fact that any tails might slip into other rows/columns. You must ensure all other positions are heads.
If multiple rows or columns can hold that single run of tails, you have to sum over all possible row or column placements.
If diagonals also matter (e.g., wanting a run of tails along a diagonal), that further complicates the counting.
These additional questions and scenarios help highlight how seemingly simple combinatorial problems around “exactly t consecutive tails” can become complicated once constraints vary or the setup changes to multiple dimensions or correlated flips.