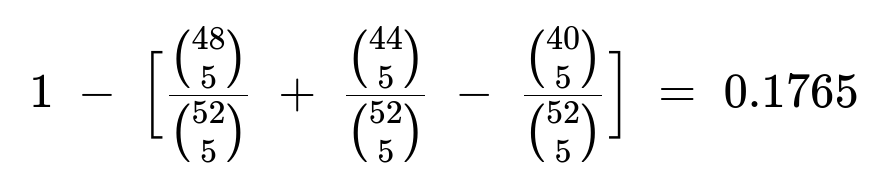ML Interview Q Series: Calculating Ace and King/Queen Hand Probability Using Inclusion-Exclusion
Browse all the Probability Interview Questions here.
You draw at random five cards from a standard deck of 52 cards. What is the probability that there is an ace among the five cards and a king or queen?
Short Compact solution
We define event A as “no ace among the five cards” and event B as “no king or queen among the five cards.” By inclusion-exclusion, the probability that we have at least one ace and at least one king or queen is:
Comprehensive Explanation
Defining the Events
Event A: “No ace in the 5-card hand.” This means we pick all 5 cards from the 52-4 = 48 non-ace cards.
Event B: “No king and no queen in the 5-card hand.” There are 8 total cards that are kings or queens (4 kings + 4 queens), so if we exclude these 8 cards, we have 44 cards left.
We want the probability that the hand contains at least one ace and at least one king or queen. In other words, we want the probability that the 5-card hand does not fall into either of the two “bad” categories: “no ace” or “no king/queen.”
Mathematically, we are looking for the probability of the complement of A ∪ B (meaning “it’s not the case that we’re missing an ace or missing both king and queen”), so:
P(at least one ace and at least one king or queen) = 1 - P(A ∪ B).
Using Inclusion-Exclusion
Recall the inclusion-exclusion principle:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B).
Hence:
P(A ∪ B) = • P(A) = number of ways to choose 5 cards out of the 48 non-aces, divided by number of ways to choose 5 cards out of 52. • P(B) = number of ways to choose 5 cards out of the 44 cards that are neither king nor queen, divided by total ways to choose 5 cards out of 52. • P(A ∩ B) = number of ways to choose 5 cards from the 40 cards that are neither ace nor king nor queen.
Therefore,
P(A ∪ B) = ( (48 choose 5)/(52 choose 5) ) + ( (44 choose 5)/(52 choose 5) ) - ( (40 choose 5)/(52 choose 5) ).
Finally, we subtract that result from 1:
P(at least one ace and at least one king or queen) = 1 - [ P(A) + P(B) - P(A ∩ B) ].
Why It Works
A hand with at least one ace and at least one king or queen is precisely the complement of “hands with no ace or no king or queen.”
If we simply added P(A) + P(B), we would be double-counting those hands that have neither an ace nor a king/queen (that set is exactly A ∩ B).
Hence, we subtract P(A ∩ B) to correct for double-counting.
Numeric Computation
(48 choose 5) counts 5-card selections from the 48 non-ace cards.
(44 choose 5) counts 5-card selections from the 44 cards that exclude kings and queens.
(40 choose 5) counts 5-card selections from the 40 cards that exclude aces, kings, and queens.
Dividing each by (52 choose 5) converts them into probabilities. The final value ends up being roughly 0.1765, or about 17.65%.
Potential Follow-Up Questions
1) What if “king or queen” meant we needed at least one king and at least one queen (instead of king or queen)?
In that scenario, we would redefine event B differently. Specifically, we might define:
B1 as “no king in the 5 cards,”
B2 as “no queen in the 5 cards.”
Then the event “no king or no queen” changes into “B1 ∪ B2.” We would compute the probability that we have at least one king and at least one queen (i.e., the complement of B1 ∪ B2) potentially using inclusion-exclusion again. This subtle change in wording—“king or queen” vs. “king and queen”—would dramatically alter our counting approach.
2) In a real interview, how might we verify the arithmetic quickly?
Often, you can do the following:
Use a quick Python script to brute force or partially check the counts.
Confirm binomial coefficients (n choose k) using a library such as
math.comb(n, k)in Python or by a direct combinatorial function.Compare your final decimal approximation to the fraction given by the exact ratio of binomial coefficients.
For instance:
from math import comb
num_ways_total = comb(52, 5)
num_ways_no_ace = comb(48, 5)
num_ways_no_kq = comb(44, 5)
num_ways_no_ace_no_kq = comb(40, 5)
p = 1 - (num_ways_no_ace + num_ways_no_kq - num_ways_no_ace_no_kq)/num_ways_total
print(p) # Should be close to 0.1765
3) Why does the counting approach rely on the complement?
Frequently, for “at least one” type problems, it is easier to count the ways in which those cards do not appear (i.e., the complement). Counting “no ace” or “no king or queen” directly often involves straightforward binomial coefficients. If we tried to count “at least one ace and at least one king/queen” directly, we would have to break it down into multiple subcases (e.g., exactly 1 ace and 1 king/queen, 1 ace and 2 kings/queens, 2 aces and 1 king/queen, etc.), which is more cumbersome.
4) Could this approach generalize to more categories of cards?
Yes. If we want to require at least one card from several different subsets (e.g., at least one spade, at least one face card, etc.), we can keep adding events and then use higher-order inclusion-exclusion. However, each extra event can complicate the expression substantially. In large-scale problems (like analyzing multi-category membership), we either rely on systematic code or adopt advanced combinatorial identities to account for every intersection accurately.
5) Any real-world mistakes to avoid?
Misinterpreting “king or queen” as “king and queen.” Always clarify the wording in probability questions.
Forgetting to include the intersection in an inclusion-exclusion approach. Skipping that step causes double counting or undercounting.
Arithmetic or combinatorial coefficient errors: these are very common. Double-check (n choose k) computations and confirm numeric results carefully.
All these follow-ups ensure you fully grasp why the formula is set up this way and how to adapt the reasoning to other probability or combinatorial questions.
Below are additional follow-up questions
1) What if we want the probability of getting at least two aces and at least two kings or queens in the 5-card hand?
When you increase the required minimum count for certain ranks, direct combinatorial enumeration becomes more involved. Specifically, you must ensure there are at least 2 aces and at least 2 cards that are either kings or queens among the 5. One way to handle this is:
Break down the hand possibilities by exactly how many aces (2, 3, 4) can fit into a 5-card hand.
For each exact count of aces, you also need to count exactly how many kings/queens fit, given there are 5 total cards.
Use binomial coefficients to count each scenario (for example, if you have 2 aces, then the remaining 3 cards must contain at least 2 kings/queens).
Sum across all scenarios to find the total valid ways.
Divide by the total number of 5-card combinations from 52.
A subtle pitfall is accidentally missing a scenario (e.g., you forget to consider the case of 3 aces and 2 kings, or 4 aces and 1 king combined with 1 queen is not possible because that would total 5). You must ensure every combination is included without double counting.
2) How would the result change if you only have a partial deck or some cards are missing?
If the deck is incomplete or you know certain cards have already been removed, you must adjust the total number of available cards and the composition of those cards. For instance, if you know one ace has been removed, then there are only 3 aces left in the deck. Similarly, if 10 random cards are removed but you don’t know which, you might need to reason with conditional probabilities or expected values over all possible sets of removed cards.
A key pitfall is failing to update both the total number of cards and the specific ranks or suits that remain. This can lead to incorrect denominators or numerators in your combinatorial counts.
3) How can we apply a hypergeometric distribution viewpoint here?
The hypergeometric distribution describes drawing k “successes” without replacement from a finite population. If we consider “ace” as a success category and “king/queen” as another category, we can set up multiple hypergeometric distributions:
One hypergeometric distribution for the number of aces.
Another for the number of kings or queens.
To combine them, you either sum over the joint probabilities or use inclusion-exclusion. You must be careful because the random variables “number of aces” and “number of kings/queens” are not independent in a 5-card draw (each card drawn affects both categories). The main pitfall here is assuming independence and trying to just multiply the probabilities. Instead, rely on careful summations or combinatorial counting that account for the overlap.
4) What if we require at least one ace exactly on the last draw and at least one king or queen somewhere in the 5 cards?
This changes the problem structure to a sequence-based perspective. You must consider:
The probability that the 5th card is an ace.
And in the first 4 cards, there is at least one king or queen.
In general, sequential draws without replacement can still be mapped to combinatorial arguments, but the condition on the last card’s identity imposes a new constraint. One approach is:
Count the ways to choose 1 ace for the 5th card and some arrangement for the other 4 cards containing at least one king or queen.
Divide by the total ways to choose and order 5 cards.
A common pitfall is forgetting that specifying the last card changes the denominator from simple combinations (choose 5 from 52) to permutations (arrange 5 from 52), or you must carefully use combinations but multiply or divide by the appropriate number of ways to order that last card.
5) How would the answer look if we consider multiple decks shuffled together?
In the case of multiple combined decks (e.g., 2 decks for a total of 104 cards), the approach is similar but with different totals:
Total cards: 104 instead of 52 (if 2 decks).
Total aces: 8 instead of 4, and total kings or queens: 16 instead of 8.
You would adjust each binomial coefficient to reflect the new numbers. The logic using events “no ace” or “no king or queen” still applies; however, you must be precise in re-counting how many of each rank are present. A pitfall is to simply scale up the deck size but forget to scale up the count of each rank.
6) How do we tackle scenarios where the probabilities of interest shift if the cards are drawn one at a time, with knowledge updated after each draw?
If you draw cards one by one and gain knowledge of what has already been drawn, the probability of a future draw containing an ace or containing a king/queen will shift dynamically. You might use conditional probability:
P(next card is an ace | we already saw k aces in the previous draws).
Or you could revert to a combinatorial perspective: the deck is now smaller, containing fewer (or the same number of) aces/kings/queens. A classic mistake is to ignore the updated deck composition. In real-time card scenarios (like card counting in blackjack), not updating your probabilities after each draw leads to incorrect estimates of your chances.
7) How does the probability change if suits are also relevant (e.g., we want at least one ace of spades and at least one king or queen of diamonds)?
You must narrow the event definitions:
“At least one ace of spades” means you want at least 1 specific card out of the entire deck.
“At least one king or queen of diamonds” means you want at least 1 card out of the 2 diamonds (king of diamonds or queen of diamonds).
One approach is to apply the inclusion-exclusion principle with events that reflect “no ace of spades” and “no king of diamonds or queen of diamonds.” Once again, the pitfall is to track each relevant card or subset properly. If there are multiple suits or multiple particular cards, the problem quickly becomes complicated, and the easiest approach can be to break it into separate smaller events, then systematically combine them with inclusion-exclusion.