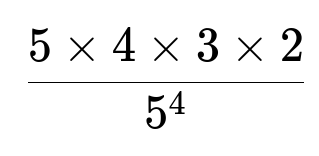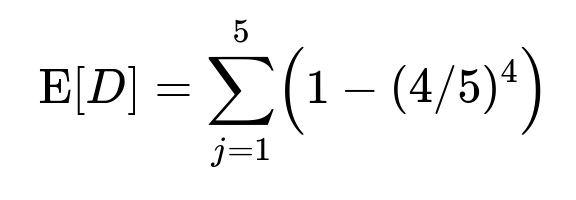ML Interview Q Series: Calculating Probability of Distinct Elevator Floor Choices Using Permutations
Browse all the Probability Interview Questions here.
Four individuals board an elevator on the ground floor of a building with five upper floors. Each person independently chooses one of these five floors at random. What is the probability that all four choose different floors to exit?
Comprehensive Explanation
This scenario involves four people selecting from five available floors in a building (excluding the ground floor). Each person is equally likely to choose any of the five floors. The event of interest is that no two people pick the same floor. In probability terms, we want all four selections to be distinct.
The total number of ways the four passengers can choose floors is 5^4. This arises because each of the four passengers has 5 possible floors to choose from, independently of one another.
The number of favorable ways, in which all four individuals end up on different floors, corresponds to the number of ways to pick a distinct floor for each person. This can be visualized as arranging 4 distinct people into 5 distinct floors without repetition. That count is 5 * 4 * 3 * 2.
The probability is therefore the ratio of the number of favorable ways over the total ways.
In the numerator 5 * 4 * 3 * 2 represents the number of permutations of 5 floors taken 4 at a time. In the denominator 5^4 is the total number of ways the four people can choose any of the 5 floors. Numerically, the probability is (5 * 4 * 3 * 2) / 5^4 = 120 / 625 = 24 / 125 = 0.192.
Each factor in the numerator can be explained as:
5 choices for the first person.
4 remaining choices for the second person.
3 remaining choices for the third person.
2 remaining choices for the fourth person.
The denominator 5^4 indicates each of the 4 people can independently select any of the 5 floors.
Deeper Insight and Potential Pitfalls
When dealing with such combinatorial probabilities, it is important to ensure that:
The independence assumption is correct. If external factors correlated the choices (for example, certain people not wanting to exit on the same floor as someone else), the calculation would differ.
The floors are indeed equally likely for each person. Real scenarios might have floors that are more popular than others.
Another subtlety is the requirement for there to be at least as many floors as people. If there were fewer floors than people (for example, if there were only 3 floors for 4 people), the probability of everyone getting off on a different floor would be zero.
Example Using Python
Below is a short Python simulation demonstrating the approximate probability that no two passengers get off at the same floor. This is done by random trials.
import random
def simulate_different_floors(num_trials=10_000_00):
count_distinct = 0
for _ in range(num_trials):
# Each passenger picks a random floor from 1..5
floors_chosen = [random.randint(1, 5) for _ in range(4)]
if len(set(floors_chosen)) == 4:
count_distinct += 1
return count_distinct / num_trials
prob_estimate = simulate_different_floors()
print("Estimated Probability:", prob_estimate)
Running this code should yield a result close to 0.192 (or 19.2%).
Follow-up Questions
How would the probability change if each floor is not equally likely?
In that case, the total number of ways remains 5^4 if we still assume independence, but each passenger’s probability distribution for choosing a floor would no longer be uniform. Suppose floor i is chosen with probability p_i for each passenger, where p_1 + p_2 + p_3 + p_4 + p_5 = 1. The probability that all four end on distinct floors would be the sum of probabilities of each distinct floor assignment, calculated by multiplying the appropriate p_i for each passenger arrangement. Specifically, you would sum p_i * p_j * p_k * p_l over all combinations of i, j, k, l that are distinct. This calculation can quickly become more complicated, but the principle remains the same: count all distinct assignments, multiply probabilities for each assignment, and sum.
Does ordering matter here when we talk about permutations?
In this context, yes. One way to see it is that the passengers are distinct (they are four different people). So for counting favorable ways, we treat them as arranged in an order (who picks first, second, etc.). Then we compare it with the total ways (which also implicitly treat each person's choice as separate). If the passengers were indistinguishable (which is rarely the case in real-life scenarios), the calculation would differ. Here, each passenger’s outcome is separate, so permutations fit the correct reasoning.
What if the building only had three floors instead of five?
If there were only three floors available for four passengers, it would be impossible for all four to exit on different floors. The probability would be zero. In general, if the number of people exceeds the number of floors, the probability of everyone choosing a distinct floor is zero.
Could this approach be generalized to more floors or more passengers?
Absolutely. For N people and K floors (with N <= K), the number of ways to choose distinct floors is K * (K - 1) * ... * (K - N + 1). The total number of ways for them to choose floors is K^N. So the probability of all different floors in that generalized scenario is (K*(K-1)...(K-N+1)) / K^N. If N > K, the probability is zero.
Below are additional follow-up questions
What if some floors are temporarily inaccessible due to maintenance? How does that change the probability?
If one or more floors are out of service, the set of available floors shrinks. Suppose only M out of the original 5 floors can actually be used (where M >= 4 to keep the possibility that all four passengers get off on different floors). The total number of ways each passenger can choose a floor becomes M^4, because each of the four passengers chooses among the M available floors.
The count of favorable outcomes (all distinct floors) is M * (M - 1) * (M - 2) * (M - 3) when M >= 4. If M < 4, that probability is zero automatically because there are not enough available floors for each person to have a unique one.
Hence, the probability that all four exit on different floors is the ratio:
M*(M - 1)(M - 2)(M - 3) / M^4
One subtlety is whether each passenger is aware of, or abides by, the maintenance restrictions. If they still “choose” from floors that are closed, that probability is not valid. In the real world, the elevator would not typically let them press a button for a closed floor. If the elevator physically prevents them from choosing a closed floor, then M is indeed the correct count of floors they can choose from.
Pitfalls might include:
If the elevator does allow pressing a disabled floor but the passenger is forced to exit at the nearest valid stop. This would invalidate the assumption of one-to-one passenger-floor choice.
If some maintenance floors are only partly inaccessible, the probability of a passenger successfully choosing such a floor might be a fraction. The problem becomes more complicated, requiring fractional probabilities or conditional scenarios.
How can we find the expected number of floors actually used by the four passengers?
Instead of just computing the probability that all four floors are distinct, we might be curious how many distinct floors are used on average. This means we want the expected value of the random variable D, which counts how many distinct floors among the five end up with at least one passenger.
A well-known approach is to use indicator variables: for each floor j in {1..5}, define an indicator I_j = 1 if at least one passenger picks floor j, and 0 otherwise. Then D = I_1 + I_2 + I_3 + I_4 + I_5. By the linearity of expectation, E[D] = E[I_1] + ... + E[I_5]. Since all floors are equally likely,
E[I_j] = P(at least one passenger chooses floor j) = 1 - P(no one chooses j).
Because each passenger independently skips floor j with probability 4/5, the probability that all four skip j is (4/5)^4. Hence for each j,
E[I_j] = 1 - (4/5)^4.
Thus,
In text form, that is 5 * (1 - (4/5)^4). Numerically, (4/5)^4 = 256/625, so 1 - 256/625 = 369/625. Multiply that by 5, and you get 1845/625 = 2.952. Therefore, on average, you can expect that about 2.952 distinct floors will be used whenever four passengers choose among five floors uniformly at random.
Potential pitfalls or edge cases:
If passengers are not equally likely to choose each floor, we must compute each E[I_j] = 1 - (1 - p_j)^4, where p_j is the probability of choosing floor j.
Correlated choices (e.g., a group traveling together) alter the probability that no one chooses a particular floor.
Can we apply inclusion-exclusion to verify or find related probabilities?
Yes. While it is straightforward to count permutations for the event “all four passengers exit on different floors,” you can also use inclusion-exclusion to compute the probability that at least two people share the same floor, then subtract from 1. For instance, define events A_{i,j} to be “person i and person j get off on the same floor.” Inclusion-exclusion helps systematically count the union of these events without double-counting overlaps.
Using inclusion-exclusion can serve as a sanity check or an alternative approach. However, it can be more cumbersome to do by hand if many passengers are involved because you have to track single overlaps, double overlaps, triple overlaps, etc. The direct permutations approach is often more succinct for the specific question of “what is the probability that all four floors chosen are distinct?”
Edge cases:
With more passengers, the complexity of inclusion-exclusion grows sharply.
If floors are not equally likely, you must incorporate p_i terms into each event’s probability carefully.
How do correlated choices among passengers (e.g., families traveling together) impact this probability?
When passengers’ decisions are not independent, the probability formula 5^4 for total ways no longer holds. For instance, a family of four might all choose the same floor more often because they have a shared destination. In other situations, people might avoid getting off on a busy floor, creating a negative correlation in choices.
Some effects:
If positive correlation is high (many people going to the same floor frequently), the probability of all-different floors is reduced.
If negative correlation is present (people deliberately avoid floors chosen by others), the probability of all-different floors is increased.
Analyzing correlated decisions usually means specifying a joint probability distribution for the four passengers’ floor selections. The counting approach must then be replaced or enhanced by that joint distribution. In practical applications, collecting data on how groups choose floors can be used to estimate or model these correlations.
How does a capacity limit for each floor affect the probability of all-different floors?
In certain buildings, floors might have regulations like “maximum of X new entrants on this floor at once.” If that limit is large enough (e.g., more than 4), it effectively does not constrain four people. But if the limit is small (for example, each floor can take only 2 new arrivals), then the event “all four choose different floors” might remain possible, but the presence of constraints for a larger group can restrict the set of feasible outcomes.
Consider a limit L on each floor that is smaller than the number of passengers. You can no longer simply say 5^4 is the total number of ways. Instead, you must exclude scenarios where a floor’s usage count exceeds L. If L is 1 and you have four passengers, ironically, this forces them all to choose different floors if a scenario is to remain valid. However, if the probability distribution initially allowed any selection from 5 floors, the total valid outcomes are fewer. Each valid outcome is a scenario in which no floor is chosen by more than L people.
In practical terms, you might solve this via combinatorial counting or constraints-based enumeration:
List all ways the four passengers can pick floors (still 5^4 in principle).
Exclude those where any floor is chosen by more than L people.
Of the remaining valid assignments, count how many correspond to distinct floor usage.
Compute the probability by dividing the count of “distinct floors” assignments by the total valid assignments.
If we repeat the scenario many times (multiple independent elevator rides), how do we track the fraction of rides with all-different floors?
Over multiple independent elevator trips, each with four new passengers, the fraction of rides that have no floor overlap tends to the true probability in the long run by the Law of Large Numbers. Specifically:
If the probability of all-different floors is p (which we have calculated as 0.192 for five floors and four passengers), then for many repeated trials, the average proportion of such “distinct floors” outcomes should be close to 0.192.
Implementation considerations:
Simulations (like Monte Carlo) can be coded to repeatedly simulate four passenger choices. Over many trials, you can approximate p by counting how often all choices differ.
In a real building scenario, you might record large-scale data over time. If you observe significant deviations from the theoretical probability, that might suggest the distribution is not uniform or the choices are not independent (e.g., many people might be traveling in pairs or going to popular floors).
Edge cases:
If the building is predominantly used for a single-floor purpose (like everyone going to a cafeteria on the top floor), empirical data will show a different fraction.
If sample sizes are too small, random variation can distort estimates of p.