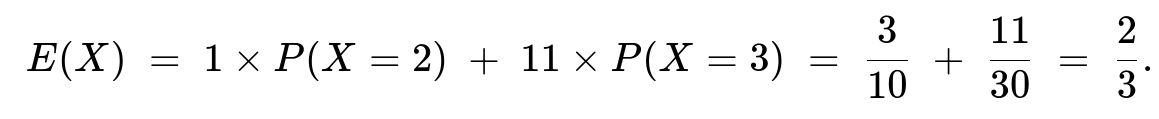ML Interview Q Series: Calculating Game House Advantage Using Expected Value and Hypergeometric Probability.
Browse all the Probability Interview Questions here.
You pay $1 to draw three balls without replacement from a box containing 10 balls in total, of which 4 are gold-colored. You get your $1 stake back if you draw exactly 2 gold balls. You win $10 plus get your $1 stake back if you draw all 3 gold balls. Otherwise, you get nothing. Find the house advantage (i.e. the percentage of your $1 stake that you lose on average when you play).
Short Compact solution
First, denote by X the random variable representing your payoff (the amount you get back in total). The probabilities of drawing exactly j gold-colored balls in a draw of 3 are:
From the binomial coefficients, we get:
P(X=2) = 3/10.
P(X=3) = 1/30.
Because the payoff is $1 when j=2 and $11 when j=3 (the extra $10 plus the original $1 stake), the expected payoff is:
Since you pay $1 to play, your average loss is 1 - 2/3 = 1/3. The house advantage, which is the fraction of your $1 stake that you lose on average, is 1/3 = 33.3%.
Comprehensive Explanation
Game Setup and Notation
We have a box containing 10 total balls, with 4 of them being gold. We draw 3 balls without replacement, and our payoff depends on how many gold balls we draw:
If we draw exactly 2 gold balls, we receive $1 (which is effectively just getting back our stake).
If we draw all 3 gold balls, we receive $11 (which is $10 profit plus our original $1 stake).
Otherwise, if we draw fewer than 2 gold balls, we get $0 back.
We denote by X the random variable for our final monetary return (the amount we get back, not our net profit). Each play costs $1 upfront. Hence, our net outcome for each play is X - 1.
Key Probability Computations
To figure out our expected return, we must compute the probabilities that X takes each value. Because we are drawing 3 balls from 10 without replacement and there are 4 gold balls in total, we can use combinatorial arguments to find these probabilities.
Probability of Drawing Exactly j Gold Balls
The number of ways to choose j gold balls out of 4 is denoted C(4, j), and the number of ways to choose (3 - j) non-gold balls out of the 6 available is C(6, 3 - j). The total number of ways to draw any 3 balls from the 10 is C(10, 3). Hence, for j gold balls, the probability is:
In particular, for j=2:
We choose 2 out of 4 gold balls (
C(4,2)) and 1 out of 6 non-gold balls (C(6,1)),The total possible draws are
C(10,3).
Similarly, for j=3:
We choose all 3 out of 4 gold balls (
C(4,3)) and 0 out of 6 non-gold balls (C(6,0)).
Payoff Values and Expected Value
Recall that our random variable X is the amount of money we get returned (not our profit). Specifically:
X = 1 when we draw exactly 2 gold balls,
X = 11 when we draw exactly 3 gold balls,
X = 0 otherwise.
Once we have the probabilities, we compute the expected return:
X * P(X) over all possible outcomes:
E(X) = 0 × P(X=0 or X=1) + 1 × P(X=2) + 11 × P(X=3).
We can find P(X=2) and P(X=3) explicitly:
P(X=2) turns out to be 3/10,
P(X=3) turns out to be 1/30.
Therefore:
House Advantage Computation
You pay $1 to play each time. The average (expected) return from the game is 2/3. Thus, on average, you lose 1 - 2/3 = 1/3. This 1/3 corresponds to 33.3% of your initial $1 stake, so the house advantage (sometimes also called the “house edge”) is 33.3%.
In other words, every $1 placed on this game yields, on average, only $0.67 back, meaning you lose $0.33 on average per play. That is the fundamental definition of a house advantage: the house edges out a profit of 33.3% on the money you bet in the long run.
Follow-up Questions
What if we changed the number of gold balls in the box?
If the box contained a different number of gold balls while still drawing 3, we would recompute the probabilities P(X=2) and P(X=3) with the new counts. The logic remains identical, but the combinatorial factors C(4, j), C(6, 3-j) would be replaced by C(G, j), C(T, 3-j), where G is the new number of gold balls and T is the number of non-gold balls (so G + T = total balls). The expected value would then be recalculated accordingly, and thus the house advantage might differ.
Why is the house advantage stated as a percentage?
Because we are typically interested in how much the house wins as a fraction of the player's original stake. If your expected return is 2/3 of the $1 you bet, then your average loss is 1/3 of your stake. Expressing 1/3 as a percentage gives 33.3%, so the house advantage is 33.3%. This is a standard practice in casino or carnival games to express how much the game “favors” the house.
If the player wants to see if the game is “fair,” what must be true?
A “fair” game implies an expected net outcome of 0 for the player. Equivalently, the house advantage would be 0%. For this game to be fair, the expected return E(X) must be exactly $1. That would require adjusting either the number of gold balls or the payoff amounts so that the final expected payoff equals the $1 stake.
How does this result hold over many rounds?
By the Law of Large Numbers, if you play the game repeatedly (many independent trials), the average net result per game will converge to the expected value in the long run. That means over a large number of plays, your total losses per play should tend to $0.33, which is the 33.3% house advantage multiplied by your $1 stake.
Could a betting strategy overcome this house advantage?
No purely probabilistic-based strategy can change the expected returns in a game like this because each draw is from a well-defined distribution and the cost remains fixed at $1. There is no advantage from any “system” for which balls are drawn. Once you pay your $1, the game’s probabilities of drawing certain numbers of gold balls are mathematically determined. Thus, the house advantage remains the same regardless of short-term winning streaks or any betting system.
Below are additional follow-up questions
How does the variance of the payoff impact the perception of the game's fairness?
One might wonder not only about the expected value of the payoff but also its variance or standard deviation, as these measures help quantify the risk or volatility in the game. Even if the expected loss is 1/3 of the stake, the distribution of outcomes can be important to a player who is risk-averse or risk-seeking.
Answer Explanation (Variance Computation and Interpretation): To calculate the variance, you would compute E(X²) - [E(X)]², where X is the payoff (0, 1, or 11). You’d first find the probabilities for X=0, X=1, and X=11, then plug them into:
E(X²) = 0² * P(X=0) + 1² * P(X=1) + 11² * P(X=11).
We already know E(X).
Once the variance is known, the standard deviation is the square root of that variance.
A high variance indicates that there is a large spread between winning big (11) and winning nothing (0). Even if the average net is a loss, some players might be attracted by the occasional high return. Conversely, others might dislike the frequent zero payoffs. While this doesn’t change the house advantage, it reveals how “swingy” the game can be.
Potential Pitfall/Edge Case:
If a game has a low house advantage but a very high variance, it can feel very “unfair” in the short run because you might experience long losing streaks. Conversely, a high house advantage game with small variance can appear more steady but still drain your bankroll slowly.
What if we change the payout structure to give smaller rewards for exactly 1 gold ball?
In some carnival games, the organizers might tweak the rules to make it seem easier to “win something.” Suppose a variant is introduced where drawing 1 gold ball still returns a small partial payout, say $0.50, while the payouts for 2 gold balls and 3 gold balls remain the same.
Answer Explanation (Impact on Expected Value): The core probability mechanism for drawing j gold balls remains the same. However, the random variable X, representing your total return, changes to:
X = 0.50 when exactly 1 gold ball is drawn,
X = 1 when exactly 2 gold balls are drawn,
X = 11 when exactly 3 gold balls are drawn,
X = 0 when no gold balls are drawn.
You would recalculate E(X) accordingly:
P(X=0.50) = Probability of drawing exactly 1 gold ball = (C(4,1) * C(6,2)) / C(10,3).
P(X=1) = Probability of drawing exactly 2 gold balls = (C(4,2) * C(6,1)) / C(10,3).
P(X=11) = Probability of drawing exactly 3 gold balls = (C(4,3) * C(6,0)) / C(10,3).
The probability of X=0 (0 gold balls) is everything else.
Adding these with their respective payoffs yields the new expected return. Whether the house advantage goes up or down depends on how these partial payouts compare to the shift in probabilities. Often, a small payout for 1 gold ball does not drastically change the overall house edge unless you are giving away enough to raise E(X) above 1.
Potential Pitfall/Edge Case:
A small “consolation” payout for 1 gold ball might be offset by decreasing payouts for 2 or 3 gold balls in some practical carnival setups, so the overall house advantage might remain the same or even increase.
Players might erroneously conclude it’s more “fair” because they “win more often,” even if the math shows the same or a higher house edge.
What if the game were played with partial replacement of the gold balls?
In some variations, after drawing each gold ball, the ball could be replaced (or not replaced) according to specific rules. For instance, if you draw a gold ball, you set it aside but immediately add a new gold ball to keep the count in the box consistent. This changes the probabilities significantly.
Answer Explanation (Analyzing Partial Replacement): With partial replacement, the state of the box changes in a different way than standard “without replacement.” Typically, you would need a step-by-step approach to track the probability after each draw. For instance:
First draw: Probability of gold is 4/10.
If gold is drawn and replaced with a new gold ball, the composition remains effectively the same: 4 gold out of 10.
Repeat the process for the second and third draws.
This approximates a scenario closer to sampling with replacement, but it’s not pure replacement if non-gold balls are left out of the replacement scheme. The expected value can be recalculated once you define the exact rules for replacement. Usually, partial replacement might increase the chance of drawing gold again (if each gold ball is replaced with another gold ball) or it could keep it constant. A thorough analysis must define precisely how replacement occurs.
Potential Pitfall/Edge Case:
If the replacement scheme is incorrectly understood, one might miscalculate the probabilities. For example, you might assume that each draw is still hypergeometric when, in fact, it moves toward a binomial setting if every gold ball is replaced.
A mismatch between how gold vs. non-gold balls are replaced can skew the distribution significantly.
What if players are allowed to see the first ball drawn before deciding to continue?
Imagine a scenario where, after drawing the first ball, you get to decide whether to “continue” (draw the remaining two balls) or “forfeit.” This is a classic conditional probability scenario that adds a strategic element.
Answer Explanation (Conditional Probability and Strategy): Normally, the game is not structured to allow a choice. But if you did allow it, you would condition your decision on the result of the first draw:
If the first ball is gold, the probability of eventually drawing 2 or 3 gold in total is now different than it was initially.
If the first ball is not gold, the probability structure also changes for the remaining draws.
By computing the expected payoff in each scenario and factoring in your choice to continue or forfeit, you can see if any advantage emerges. Typically, the carnival would not offer you such an option because it might let a well-informed player reduce the house advantage. The game’s value to the house is partially that no strategic decisions can be made after you have new information.
Potential Pitfall/Edge Case:
If the carnival sets an additional cost for continuing, you need to incorporate that cost into your expected value calculation. The house could still preserve an advantage by setting that continuation fee in such a way that your expected gain remains below your stake.
In real-world carnival games, you usually do not get partial information mid-draw, so this scenario is more theoretical than practical.
Could mislabeling or defective gold balls affect the probabilities?
In a real-world setting, what if some gold balls are not clearly identifiable, or there's a manufacturing defect making some gold balls appear faded or partially colored?
Answer Explanation (Practical Accuracy of Probability): The entire calculation hinges on the assumption that there are exactly 4 identifiably gold balls and 6 clearly non-gold balls. If a ball’s color is ambiguous, or there is human error in counting, the probability distribution might shift slightly. You might not have precisely 4 gold and 6 non-gold, leading to different outcomes:
If actually there are only 3 real gold balls and 1 “faded” ball that players cannot reliably classify, the effective probability of drawing a “true gold” changes.
Over many plays, small miscounts can accumulate and yield a different house edge than the theoretical 33.3%.
Potential Pitfall/Edge Case:
If the carnival intentionally mislabels balls (e.g., painting them gold but counting them as non-gold internally), the official rules say 4 gold exist, but in practice, you might always be at a disadvantage. This crosses into fairness and trust issues, making the real mathematics irrelevant if the underlying assumptions are violated.
How might scaling up the draws (e.g., drawing 5 or more balls) affect the house advantage?
Sometimes carnival operators might tweak the game to draw more balls (5 out of 10, or even 6 out of 15, etc.). How does that scale the probabilities and payouts?
Answer Explanation (Generalizing Combinatorial Logic): The same hypergeometric distribution logic applies:
The probability of drawing exactly k gold balls out of n drawn from a total of G gold and T non-gold (where G + T is the total in the box) is given by (C(G,k) * C(T, n - k)) / C(G + T, n).
The key difference is that you must redefine the payout structure for each number of gold balls. For instance, if you draw 5 balls, do you pay out for exactly 3 gold, exactly 4 gold, or all 5 gold being gold? Once you define the new payoff schedule, you can compute E(X) the same way: sum over the payoffs times their probabilities. In many extended-draw scenarios, the house will adjust the payoffs to ensure they keep a margin.
Potential Pitfall/Edge Case:
If the number of gold balls or total draws is large, the calculations might seem more cumbersome. Mistakes in combinatorial logic can happen easily.
The game might appear more exciting or have more “ways to win,” but if the payoff doesn’t sufficiently compensate for the lower probabilities, the house edge can remain high or even become higher.
What if the player can buy insurance after seeing some partial outcome?
Some casinos or carnival games allow a side bet—often called “insurance.” For instance, you pay an extra fee after the first draw to insure against not drawing enough gold balls. This changes the overall expected value for the player in a complex way.
Answer Explanation (Side Bets and Conditional Bets): With insurance, you typically pay a side bet that yields a certain return if a specific undesirable event happens (like failing to draw 2 or 3 gold by the last draw). The mathematics involves conditional probabilities: once you see the first draw’s outcome, you update your probabilities for the remaining draws. Then you decide if the side bet is worth the cost. Usually, the side bet is priced so that the house still maintains (or increases) its advantage overall:
Compute P(no more gold in next draws | current drawn ball is gold or not gold).
Price the insurance so that your expected gain from that side bet is negative from the house's perspective.
Potential Pitfall/Edge Case:
Players might be tempted to always or never buy insurance, but the correct approach (if you aim to maximize expected value) is to compare the cost of insurance to the updated probability of the event you’re insuring against. The house often sets the insurance premium at a level that still yields a profit for them.
Over multiple plays, side bets can drain a bankroll faster if they have a higher house edge than the main game.