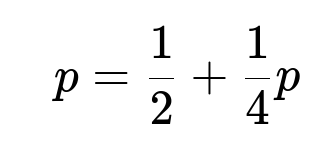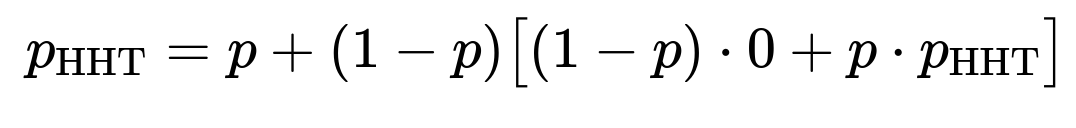ML Interview Q Series: Calculating HHT vs HTT First Appearance Probability Using Markov Chains
Browse all the Probability Interview Questions here.
What is the probability that HHT appears before HTT in a random sequence of coin tosses using Heads (H) and Tails (T)?
Short Compact solution
One can notice that both HHT and HTT require at least one initial H to begin forming their patterns, so any flips of T before the first H are irrelevant. After the first H is observed, consider the next flip:
If it is H, then HHT will definitely appear first, because the next T completes the sequence HHT. This occurs with probability 1/2.
If instead the next flip is T, two further possibilities emerge:
If the following flip is T again (TT), then HTT is completed first (probability 1/4).
If the following flip is H (TH), we effectively return to the same situation of having just seen a single H (the state after the very first H).
Let p be the probability that HHT occurs before HTT once the first H has already appeared. Then:
Comprehensive Explanation
One way to interpret why HHT wins out with probability 2/3 is to analyze the progress of partial matches for the two patterns. Both patterns share the initial "H," so you only begin tracking differences once you have that first "H." From that point onward:
If the coin toss yields another H, you are one step away from completing HHT, because you only need a T to finalize HHT. Once the pattern "HH" is observed, the first T that follows guarantees HHT, which occurs before any chance to pivot to HTT.
If the coin toss yields T right after seeing one H, then you have "HT." From here, you check the next flip:
If it is T, the pattern HTT appears right away, so HTT wins in that sub-branch.
If it is H, you effectively have the situation "TH" which effectively resets you back to seeing a lone H at the end of the partial string, re-entering the same analysis as the original "first H" state.
A more formal approach is to define states based on what partial sequences have been observed, then set up equations describing the transition probabilities between states. Solving these leads to the same 2/3 result.
The key points are that you ignore leading tails, the pattern "HH" gives a direct advantage to HHT, and a single "HT" can transition either into a win for HTT or reset to a scenario indistinguishable from the initial single "H" state. These observations lead to the concise probability computation described above.
What if the coin is biased rather than fair?
If the coin is biased such that it lands Heads with probability p and Tails with probability 1−p, we need a similar state-based or partial pattern approach, but with different probabilities for moving through the states. For instance:
After the first Head, the next flip is Head with probability p and Tails with probability 1−p.
If the second flip is Head, you await a T to complete HHT, with probability 1−p on each flip.
If the second flip is T, you then look at the third flip, which can be T (with probability 1−p) to give HTT, or H (with probability p) to move back to effectively a single Head at the end.
How can we be sure about the result?
One sanity check is to perform a computational simulation. You can simulate many coin flip sequences, check which pattern appears first, and approximate the relative frequency of HHT vs. HTT. As the number of trials grows large, the empirical frequency of HHT appearing first will approach 2/3.
A simple Python simulation could look like this:
import random def simulate(num_trials=10_000_00): count_hht_first = 0 for _ in range(num_trials): seen = [] found_hht = False found_htt = False while not (found_hht or found_htt): flip = 'H' if random.random() < 0.5 else 'T' seen.append(flip) # Check last three flips if len(seen) >= 3: last_three = ''.join(seen[-3:]) if last_three == 'HHT': found_hht = True elif last_three == 'HTT': found_htt = True if found_hht: count_hht_first += 1 return count_hht_first / num_trials prob_estimate = simulate() print(prob_estimate)Over a large number of simulations, this should yield a number close to 0.666..., demonstrating that 2/3 is the correct result.
How does partial matching logic help in other pattern problems?
Partial matching logic is crucial in many pattern-finding tasks known as Penney’s Game type scenarios. The technique of building states based on how many characters of the pattern have been matched so far allows you to handle overlaps in the patterns. In this specific example, HHT and HTT share common partial prefixes that cause interesting reset behaviors. In other scenarios, you can have more complicated overlaps, requiring a more detailed state machine or an automaton to track these overlaps. The same fundamental Markov chain idea applies, and you typically end up solving linear equations for the probabilities of eventually hitting one pattern before the other.
Is there a simpler way to see that HHT is more likely to appear first?
A streamlined intuitive explanation is that HHT is “quicker” to close out once you have two heads in a row. Once you see "HH," the very first T that comes along immediately finalizes HHT. In contrast, for HTT to finalize after seeing "HT," you need two specific Tails in succession without a Head interrupting the pattern. The presence of that second Head possibility in the intermediate step effectively resets you back to an "H" condition, often swinging advantage to HHT.
Could this reasoning be extended to patterns of different lengths?
Yes, you can extend this logic to arbitrary coin flip patterns of any length. You would track states based on the currently matched prefix for each pattern. For every coin flip, you transition to the next state based on whether your partial pattern matches a longer prefix or resets. Then, when a complete pattern is recognized, that pattern is declared the “winner.” For more complex patterns, the state machine can have many states if there are multiple overlaps. The underlying principle—computing probabilities of pattern completion using Markov chain transitions—remains the same.
Below are additional follow-up questions
What if the coin tosses are correlated rather than independent?
In many real scenarios, flips can be correlated (e.g., a physical coin may stick to a face more if it landed on that face in the previous toss). In such a situation, the probability of getting H or T on the next toss might depend on the outcome of the previous toss or even multiple previous tosses.
When correlation is present, the standard Markov chain approach for independent flips no longer directly applies. Instead, you might need a higher-order Markov chain that captures how states transition based on recent flip history. For example, if the probability of flipping H after H is different from the probability of flipping H after T, you need to incorporate these conditional probabilities into a more complex state transition system. Each state would encode not just the sequence of last few flips but also the possible memory effect leading to future flips.
A subtle pitfall in correlated scenarios is that one cannot simply say "the first H is guaranteed to appear eventually with probability 1," because correlation could (in pathological cases) lead to extremely long runs of T. If it is still guaranteed that all infinite sequences are possible (even if some are just less likely), then eventually H or T will appear, but the timescale and likelihood might be very different. Hence, the state transition probabilities must be carefully defined for the correlated process, and the resulting system of equations might be much larger and more complex.
How does truncating the sequence affect the analysis?
If the sequence is truncated—meaning there is only a fixed number of coin tosses allowed (say N tosses) instead of an infinite sequence—there is a possibility that neither HHT nor HTT appears within those N tosses. In that case, you might define the probability that HHT occurs first as the proportion of all possible outcomes (up to length N) where HHT appears before HTT, excluding or including any sequences in which neither occurs (depending on your definition).
One edge case is if you observe only a few tosses, for example fewer than 3. Then obviously neither pattern can appear, so the probability of “HHT before HTT” could be undefined or zero. For large but finite N, you can still set up a state-based approach or brute-force enumeration of all possible sequences of length N. When enumerating, you must carefully record when HHT or HTT first appears. If you reach the end without seeing either pattern, that outcome might be removed from the sample space (if you only care about the relative likelihood of which pattern appears first) or it might be included as a third category (“no pattern seen”).
A subtle pitfall is incorrectly counting sequences in which both patterns appear but failing to track which one appeared first. Carefully ensuring you only count the initial time one of the patterns appears is crucial.
What if we consider more than two patterns and want to know which appears first?
Sometimes, you might be interested in three or more distinct patterns—e.g., HHT, HTT, THH, and so on. You might want to know the probability distribution of which of those patterns appears first in a sequence of coin tosses. The approach is an extension of the two-pattern scenario:
Construct a state machine that tracks how much of each pattern has been matched so far.
Because multiple patterns can partially overlap among themselves and with each other, you generally need to consider the union of these overlaps.
As soon as you fully match any one pattern, you exit the chain with that pattern as the “winner.”
This can get complicated if the patterns have significant overlap. A common pitfall is incorrectly handling mutual overlap, where the partial match for one pattern might also be a partial match for another, and you jump to the wrong next state. Properly coding these transitions typically requires a systematic approach, such as the Aho–Corasick algorithm for multiple pattern searching. In a random-toss scenario, you would then incorporate the probability transitions into the Aho–Corasick structure to compute the overall chance each pattern wins first.
How do overlapping patterns create unexpected outcomes?
Overlapping patterns can arise if, for instance, you compare HHH and HHHH, or you compare patterns like HTH and THH that share subparts. In such cases, the arrival of certain flips can create a situation where you instantly pivot from partially matching one pattern to partially matching another. This can lead to outcomes that are unintuitive.
For example, a pattern could partially match itself in a way that skipping just one flip transitions you back into a strong partial match for the same pattern. Another subtle situation is when two patterns share a suffix-prefix relationship, so that once you almost complete one pattern, you are also halfway toward completing the other. Hence, analyzing which pattern wins first can require building a careful overlap transition diagram. A frequent pitfall is overlooking the fact that “resetting” to an earlier partial match does not necessarily mean you lose all progress toward completing a pattern—it might mean you switch to progress in the other pattern, or you remain in a partial match for the first pattern.
What if we want the expected time until one of the patterns appears?
In addition to wanting to know the probability that HHT appears before HTT, an interviewer might ask for the expected number of coin flips needed to see one of them appear, or specifically the expected time until the “winning” pattern first occurs.
You can still use a Markov chain or state-based approach but now you add equations for the expected time to absorption from each state. For instance, if E(S) is the expected time from some state S, and you know the probabilities of transitioning to other states along with the probability of completing a pattern, you can formulate a system of linear equations such as:
Pitfalls here include confusing the time to the first occurrence of a pattern with the time to the next occurrence. Also, if an infinite sequence is theoretically possible, you must ensure that your Markov chain is absorbing, meaning from each non-terminal state there is some chance to move eventually to a terminal (pattern-completion) state, so the expected time is finite.
What if the coin is not just Heads or Tails but has more sides or possible outcomes?
Imagine a scenario where instead of a binary coin, you have a 3-sided or 4-sided “die-like” object with outcomes labeled, say, H, T, and X. Then the patterns of interest might involve these extra symbols, for instance “HHTX” vs. “HTTX.” The approach is effectively the same: treat each side as a possible symbol in the sequence and set up a Markov chain for pattern matching with multiple characters.
The tricky part is you might have more complex transitions, since each flip can go into more branches. If the random mechanism is still memoryless with some probabilities for each side, you can handle it in a straightforward manner. A subtlety is ensuring you handle partial matches that might still line up with more than one pattern if X can appear in the middle of an otherwise H/T pattern. Each additional symbol can compound the number of states you need to track for overlaps, so complexity can grow.
How do we handle partial or noisy observations of the sequence?
Sometimes you don’t observe every flip with perfect clarity. You might see some flips but miss others, or occasionally see “H” when it was really “T” (an observation error). This complicates the question of which pattern appears first, because you could misjudge the partial sequence you have seen.
In the case of missing data (e.g., you only see a flip outcome every other time), you can either:
Model the unobserved flips as random and adjust the transition probabilities to reflect partial knowledge.
Use a Hidden Markov Model (HMM) approach in which the true coin toss outcomes are hidden states, and your observations are noisy emissions.
A major pitfall is incorrectly believing that seeing a partial sequence of H or T with some missing flips means you can definitively track the pattern’s progress. In reality, unobserved flips might have completed one pattern or the other without your knowledge. Handling this properly often involves computing probabilities over all possible hidden states consistent with your observations up to a certain point.
What if one pattern is contained within the other?
Consider a situation where you look at patterns HHT and HHTT. Notice that HHTT contains HHT as its prefix. If you are comparing which appears first, it might seem that HHT always appears first if HHTT eventually appears—because the second pattern’s first three flips match the first pattern.
However, a subtlety is that to “win,” the pattern must appear fully for the first time as a continuous block of flips. If HHT appears at positions 5–7, you declare it a “win” for HHT. If HHTT appears at positions 5–8, that also includes HHT at 5–7, meaning HHT is discovered first, so HHT wins. In that sense, the containing pattern is at a disadvantage because the embedded pattern “interrupts” it.
A pitfall is ignoring the possibility that the larger pattern might appear in a shifted fashion that partially overlaps with the smaller pattern but doesn’t strictly contain it in the same segment. This can lead to more complicated partial matches or a “reset” that ultimately allows HHTT to appear unexpectedly. When patterns are contained or partially contained within each other, you must handle the boundary cases carefully.