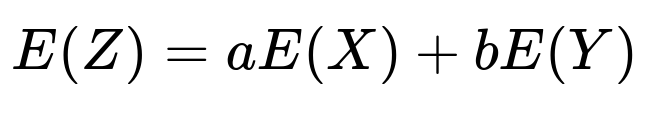ML Interview Q Series: Calculating Mean and Variance for Linear Combinations of Independent Normal Variables.
Browse all the Probability Interview Questions here.
Suppose X and Y are independent normal random variables, where X has mean 3 and variance 4, and Y has mean 1 and variance 4. Determine the mean and variance of the random variable 2X - Y.
Comprehensive Explanation
When we have a linear combination of two independent normal random variables (for example, 2X - Y), the result is also a normally distributed random variable. The mean and variance of this new variable can be derived from the properties of expectation and variance as follows:
Mean of 2X - Y
The expectation of a linear combination of random variables aX + bY is given by aE(X) + bE(Y). Here, a = 2 and b = -1.
where Z = 2X - Y. In our case, E(X) = 3 and E(Y) = 1. Substituting these in:
E(Z) = 2 * 3 + (-1) * 1 = 6 - 1 = 5.
Hence, the mean of 2X - Y is 5.
Variance of 2X - Y
Because X and Y are independent, the variance of aX + bY is a^2 Var(X) + b^2 Var(Y). Here, again a = 2 and b = -1.
Given Var(X) = 4 and Var(Y) = 4, we plug these in:
Var(Z) = 2^2 * 4 + (-1)^2 * 4 = 4 * 4 + 1 * 4 = 16 + 4 = 20.
Hence, the variance of 2X - Y is 20.
Therefore, if X ~ N(3, 4) and Y ~ N(1, 4), and they are independent, then 2X - Y follows a normal distribution with mean 5 and variance 20.
Follow-up Questions
Why is 2X - Y still normally distributed?
When X and Y are normal and independent, any linear combination aX + bY remains normally distributed. This is due to the fact that the normal distribution is closed under linear combinations. Even if we have multiple independent normal variables, summing or subtracting them (with constant coefficients) preserves normality. If X and Y were not normal, the distribution of 2X - Y might not be normal.
What if X and Y are not independent?
If X and Y are correlated (not independent), the variance of aX + bY includes the covariance term. Specifically, the general variance formula for aX + bY is a^2 Var(X) + b^2 Var(Y) + 2ab Cov(X, Y). Hence, when X and Y have some correlation, we must consider Cov(X, Y) in the calculation.
How would this change if the distributions are not normal?
For non-normal distributions, a linear combination does not necessarily follow the same family of distributions. You would need additional assumptions or apply something like the Central Limit Theorem (CLT) if you have a large enough number of i.i.d. random variables. For two random variables specifically, without normality, the exact distribution could be much more complicated.
Could you show a quick Python snippet to verify these theoretical results?
import numpy as np
# Number of samples
N = 10_000_00
# Generate samples for X and Y
X = np.random.normal(loc=3, scale=np.sqrt(4), size=N)
Y = np.random.normal(loc=1, scale=np.sqrt(4), size=N)
# Form Z = 2X - Y
Z = 2*X - Y
# Empirical mean and variance
empirical_mean = np.mean(Z)
empirical_var = np.var(Z, ddof=1)
print("Empirical Mean of 2X - Y:", empirical_mean)
print("Empirical Variance of 2X - Y:", empirical_var)
By running this code, you would observe that the empirical mean is close to 5 and the empirical variance is close to 20, confirming the theoretical derivation.
Below are additional follow-up questions
How can we derive the moment generating function (MGF) of 2X - Y?
The moment generating function of a random variable Z is defined as E[exp(tZ)]. For normally distributed Z, the MGF has a specific closed form. Suppose Z = 2X - Y. Since X and Y are independent normal variables, Z is also normal.
Here Mean(Z) = 5, Var(Z) = 20. So the MGF is: M_{Z}(t) = exp( t*5 + (1/2) * t^2 * 20 ).
Potential Pitfalls and Edge Cases:
If the distributions were only approximately normal or had heavy tails, the empirical MGF might deviate significantly for large t, reflecting tail behaviors.
If X and Y are not independent, you would need the covariance term in the exponent for the combined variable’s MGF.
In real-world scenarios with limited data, estimating the MGF empirically can be numerically unstable for large t values (due to exponential blow-up).
What happens if the means or variances are estimated from data rather than known?
In many practical situations, the true means and variances of X and Y are not known but are estimated from samples. For example, we might have sample means mX, mY and sample variances sX^2, sY^2. Then we would estimate the distribution of 2X - Y as approximately normal with mean 2mX - mY and variance 4sX^2 + sY^2 (assuming independence).
Potential Pitfalls and Edge Cases:
Sampling error in estimating the means and variances can lead to uncertainty in the final distribution for 2X - Y, especially with small sample sizes.
If the sample sizes for X and Y are drastically different, the variance estimates might be imbalanced, skewing the final distribution’s variance.
If outliers exist in X or Y, the variance estimates can be inflated, affecting the reliability of the normal assumption.
How would a small sample size affect the validity of the normal assumption?
Even though X and Y are theoretically normal, in practice we only get finite samples. If the sample size is small, conventional statistical tests (like Shapiro–Wilk) might have insufficient power to verify normality. Additionally, the sample mean and sample variance might be poor estimators for the true distribution parameters, causing a mismatch between the theoretical and observed distribution.
Potential Pitfalls and Edge Cases:
With very few data points, the Central Limit Theorem arguments used to justify normality become weak, and the observed data might not reflect the true underlying normal distribution.
In cases of extremely small data sets, confidence intervals for the estimated mean and variance could be very wide, causing large uncertainty in the distribution of 2X - Y.
If the data is skewed or exhibits kurtosis, the normal assumption breaks down more severely in small-sample regimes.
Can we test the assumption that 2X - Y is normal using real-world data?
Yes, we can apply normality tests (like the Kolmogorov–Smirnov test, Anderson–Darling test, or Q–Q plots) to samples of Z = 2X - Y generated from real data. If the p-value from these tests is sufficiently high, it supports the hypothesis of normality.
Potential Pitfalls and Edge Cases:
Normality tests may fail to reject the null hypothesis due to insufficient sample size (lack of statistical power), not necessarily because the data is truly normal.
Real-world data often have tails heavier than normal (e.g., financial returns), so a normality test could reveal that 2X - Y shows substantial deviation in the tails.
Mixed distributions or data from processes that combine different underlying regimes can invalidate a single Gaussian assumption.
What if X or Y are truncated or censored in real data?
Truncation or censoring means that for certain values (like extremely low or high observations), the data is either not observed or is aggregated (e.g., “less than 0”). This happens in numerous fields, such as medical studies with detection limits or insurance data with maximum coverage limits.
Potential Pitfalls and Edge Cases:
If either X or Y is truncated, the resulting distribution of 2X - Y will not strictly follow a normal distribution, because truncated normal variables are no longer normal in the usual sense.
Censoring can bias both the mean and variance estimates, potentially leading to an underestimation or overestimation of variance for Z = 2X - Y.
Care must be taken to use specialized methods (like maximum likelihood estimation for truncated normals or survival analysis techniques) to properly account for the missing or censored regions.
How would outliers or heavy tails in X or Y affect the distribution of 2X - Y?
In theory, if X and Y are truly normal, outliers in the data might simply be rare draws from the tails. However, real data might have heavier tails than a normal distribution.
Potential Pitfalls and Edge Cases:
A small number of extreme values in X or Y can create large fluctuations in 2X - Y since we are combining them linearly. This can significantly impact the sample variance.
If X or Y follow a distribution with heavier tails, the sum or difference is likely to exhibit even heavier tails, breaking the normal assumption.
Robust statistical techniques (e.g., using trimmed means or winsorizing outliers) might be necessary if the data has real outliers that do not conform to the hypothesized normal distribution.
What if we needed the conditional distribution of 2X - Y given X or given Y?
In some scenarios, one might need P(2X - Y <= z | X = x0) or similar. Because 2X - Y = 2x0 - Y for a given value of X, that conditional distribution depends solely on Y with a shift of 2x0.
Potential Pitfalls and Edge Cases:
If X and Y are not truly independent, conditioning on one impacts the distribution of the other. Then one needs to use the joint distribution of (X, Y).
In real-world problems, partial knowledge about one variable might be uncertain or itself estimated, requiring further Bayesian or frequentist adjustments for that uncertainty.
If Y has a distribution that deviates from normal, the conditional distribution of 2X - Y would not be a simple shift. Additional modeling is needed.
Could 2X - Y serve as a proxy for some real-world measurement, and what could go wrong?
2X - Y might represent a practical calculation, such as net profit (two sources of revenue minus one cost) or combined sensor readings (two measurements from one sensor minus an offset from another).
Potential Pitfalls and Edge Cases:
If the real-world process generating X or Y changes distribution over time (non-stationary processes), the assumption of stable means and variances breaks down, rendering the old estimates invalid.
X and Y might depend on each other through external factors, even if direct correlation is low. This hidden dependency can bias the distribution of 2X - Y.
If there is any non-linear transformation in the real measurement process, the linear approach might misrepresent the data.
How might we construct confidence intervals for 2X - Y in practice?
To build confidence intervals for Z = 2X - Y, we would typically use the normal distribution with the estimated mean and variance from sample data. For example, a 95% confidence interval might be:
2mX - mY ± 1.96 * sqrt(4sX^2 + sY^2)
assuming large enough samples for the normal approximation.
Potential Pitfalls and Edge Cases:
If sample sizes are small, the t-distribution might be more appropriate (though it is typically derived under assumptions about sample means, not direct knowledge of normal distributions).
Failure to account for sampling error or correlation (if X and Y are not truly independent) can make these confidence intervals too narrow or too broad.
If the variance estimates are skewed due to outliers, the resulting confidence intervals might fail to cover the true parameter more often than the nominal rate (e.g., 95%).
If we wanted to simulate from the distribution of 2X - Y, how would we proceed?
If X and Y are truly normal and independent, one can draw samples of X and Y from their respective normal distributions (N(3, 4) and N(1, 4)) and compute 2X - Y for each pair. This generates an empirical sample of 2X - Y. Alternatively, one could directly sample from N(5, 20) since the mean and variance are known.
Potential Pitfalls and Edge Cases:
Programming errors or misuse of pseudo-random number generators can lead to subtle biases, especially if random seeds or distribution parameters are not set correctly.
If the real-world distributions deviate from normality, the synthetic data from a perfect normal will fail to capture extreme events.
Memory and computational constraints can arise for large-scale simulations or extremely large sample sizes.