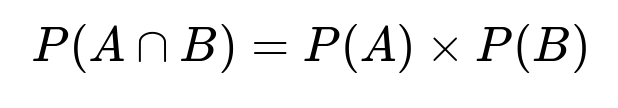ML Interview Q Series: Calculating Combined Event Probabilities Using Sample Spaces and Independence Rules.
Browse all the Probability Interview Questions here.
A fair coin is tossed, and a fair die is thrown. Write down sample spaces for (a) the toss of the coin; (b) the throw of the die; (c) the combination of these experiments. Let A be the event that a head is tossed, and B be the event that an odd number is thrown. Directly from the sample space, calculate P(A ∩ B) and P(A ∪ B).
Short Compact solution
(a) The sample space for the coin toss is {Head, Tail} (b) The sample space for the die throw is {1, 2, 3, 4, 5, 6} (c) The combined sample space is the set of all pairs (die outcome, coin outcome), for example: {(1, Head), (1, Tail), (2, Head), (2, Tail), …, (6, Head), (6, Tail)}
Let A = event that the coin shows Head, B = event that the die shows an odd number. From the sample space, we see that P(A) = 1/2 and P(B) = 1/2. Because the coin toss and die throw are independent, P(A ∩ B) = 1/4. Also, P(A ∪ B) = P(A) + P(B) − P(A ∩ B) = 3/4.
Comprehensive Explanation
The Sample Spaces
When dealing with two independent experiments—a coin toss and a die roll—the full experiment’s sample space is the Cartesian product of each individual sample space.
Coin: The coin toss has two equally likely outcomes: Head and Tail.
Die: The six-sided die (assumed fair) has outcomes 1, 2, 3, 4, 5, and 6, each with probability 1/6.
Combined: When we combine them, every pair (die outcome, coin outcome) is a distinct point in the sample space. Thus, there are 2 × 6 = 12 equally likely outcomes.
Defining Events
Event A: Coin shows Head. In terms of the combined sample space, A is {(1, Head), (2, Head), …, (6, Head)}.
Event B: Die shows odd number. In terms of the combined sample space, B is {(1, Head), (1, Tail), (3, Head), (3, Tail), (5, Head), (5, Tail)}.
Probability of A and B
From the combined sample space perspective:
P(A) = (Number of outcomes with Head) / (Total number of outcomes) = 6/12 = 1/2.
P(B) = (Number of outcomes with odd die result) / (Total number of outcomes) = 6/12 = 1/2.
Since the coin toss does not affect the die and vice versa, A and B are independent events. This allows us to use the standard formula for independent events:
Where
P(A ∩ B) is the probability that both A and B occur simultaneously (i.e., coin is Head and die is odd).
P(A) is the probability that the coin shows Head.
P(B) is the probability that the die shows an odd number.
Substituting the values:
P(A) = 1/2
P(B) = 1/2
Hence, P(A ∩ B) = 1/2 × 1/2 = 1/4.
Probability of A ∪ B
To find the probability that either A or B (or both) occurs, we use the general formula for the union of two events:
Where
P(A ∪ B) is the probability that at least one of A or B occurs.
P(A) and P(B) are as defined above.
P(A ∩ B) is the probability that both occur.
Substituting:
P(A) = 1/2
P(B) = 1/2
P(A ∩ B) = 1/4
So P(A ∪ B) = 1/2 + 1/2 − 1/4 = 3/4.
Why They Are Independent
The coin toss outcome has no influence on the die roll, and each of the 12 outcomes is equally likely. Consequently, for any event involving the coin, the probability of any event on the die side remains unchanged. Formally, events A and B satisfy:
P(A ∩ B) = P(A) × P(B),
which is the hallmark of independence.
Follow-up question 1: What if the coin is biased?
If the coin is biased, then P(A) (the probability of Head) is not 1/2. Suppose the probability of Head is p and the probability of Tail is 1 − p. The die is still fair, so P(B) = 1/2 remains the same. The sample space still consists of 12 equally distinct outcomes, but their probabilities are not all 1/12 anymore because the coin outcomes now have different probabilities.
P(A) = p
P(B) = 1/2
If the coin and the die remain independent experiments (the bias in the coin does not affect the die), then:
P(A ∩ B) = p × 1/2 = p/2, P(A ∪ B) = p + 1/2 − (p/2) = p/2 + 1/2.
So the numeric result 1/4 for the intersection would change to p/2, and the union would be p/2 + 1/2.
Follow-up question 2: How does independence differ from mutual exclusivity?
Two events are mutually exclusive if they cannot occur at the same time (their intersection is empty). In that case, P(A ∩ B) = 0.
Two events are independent if knowing one event occurred does not change the probability that the other event occurs. In that case, P(A ∩ B) = P(A) × P(B).
Mutual exclusivity implies that if one event happens, the other cannot happen. This is completely different from independence. In fact, for non-trivial events (with probabilities not zero), if they are mutually exclusive, they cannot be independent because P(A ∩ B) = 0 would contradict P(A) × P(B) > 0.
Follow-up question 3: What if we repeat these experiments multiple times?
If we repeat the process (toss the coin and throw the die) n times, the total sample space has 12^n possible sequences of outcomes (assuming the coin and die remain fair and identical in each trial). Each trial is independent from the previous, so the probability of any particular sequence is (1/12)^n under the fair coin and fair die assumption.
You could then define events like “the number of heads in n tosses is exactly k” or “the number of odd results in n die throws is m,” and calculate corresponding probabilities using binomial distributions. For combined events, as long as each trial is independent from the others, standard rules of probability (product rule, binomial formula, etc.) apply.
Follow-up question 4: Are there real-world pitfalls when assuming a fair coin or fair die?
In reality, coins can be slightly unbalanced, and dice can be biased due to imperfections in weight distribution or surface wear. It is crucial to verify fairness by empirical testing, especially in applications where the outcomes of these random variables have significant consequences. One might conduct a large number of test tosses or rolls to estimate the empirical distribution and confirm that the probability is close to the ideal 1/2 or 1/6 for each outcome.