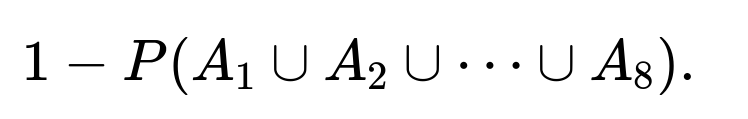ML Interview Q Series: Calculating Probability of No Married Couples on Teams Using Inclusion-Exclusion Principle.

Browse all the Probability Interview Questions here.

Twelve married couples participate in a tournament. The group of 24 people is randomly split into eight teams of three people each, where all possible splits are equally likely. What is the probability that none of the teams has a married couple?

Short Compact solution

Define event A_i as “Team i includes at least one married couple.” We want the probability that no team includes a married couple, which is

Compute each probability needed for the inclusion-exclusion principle:

• For any single team i, P(A_i) = (12 × 22) / C(24,3).

• For any i < j, P(A_i ∩ A_j) = (12 × 11 × 20 × 19) / [C(24,3) × C(21,3)].

Similarly, one can compute higher-order intersections for i < j < k, etc. After applying inclusion-exclusion, we get

P(A₁ ∪ A₂ ∪ ... ∪ A₈) ≈ 0.6553,

so the desired probability is 1 - 0.6553 = 0.3447.

Comprehensive Explanation

Defining the events

We label each of the eight teams by i = 1, 2, …, 8. Let A_i be the event “Team i contains at least one married couple.” Our goal is to compute:

Since the total group of 24 people is randomly split into eight distinct teams of three, all ways to partition the 24 people into these teams are considered equally likely.

Probability of A_i

Event A_i occurs if the three people in team i include both members of at least one of the 12 couples. There are C(24,3) ways to choose 3 people from 24 for team i. The number of ways to get at least one married couple in those 3 people is computed by first picking which couple is in team i and then choosing a third person who is not the spouse of that couple’s partner.

• We have 12 choices for the specific couple.

• After choosing a particular couple, we have 22 remaining people (excluding that entire couple) to choose as the third member.

Therefore,

In plain-text form, the denominator C(24,3) = 24! / (3!·21!) is the total number of ways to form a team of size 3 from 24 people.

Probability of A_i ∩ A_j

We also need the probability that two distinct teams, i and j, both have at least one married couple. The event A_i ∩ A_j means team i has at least one married couple and team j has at least one married couple. Because of the partitioning constraint (i.e., no overlap of players among different teams), the calculation involves:

• First forming team i with a married couple (12 ways to choose which couple) and 1 extra person from the remaining 22 individuals (so that team i definitely has that couple).

• Then for team j, we must form another triple from the remaining 21 people who were not assigned to team i. We choose one of the remaining 11 couples (since one couple is already used up in team i) and then pick 1 more person from the remaining 19 who are not that couple’s spouse.

Hence, the number of ways for two teams i and j to both have married couples can be tracked as:

• 12 × 22 ways to form the “couple + 1 extra” for team i.

• 11 × 19 ways to form the “couple + 1 extra” for team j (since one full couple and one additional person are already taken).

And the denominator must reflect the total ways of choosing teams i and j successively. We get

(The factor 20 in the numerator comes from the fact that to form team j you choose which couple among the remaining 11 couples, and you still must pick 1 person out of the 20 people left after removing that chosen couple’s two members from the pool of 21. Then that 1 chosen person is not that couple’s spouse, leaving 19 valid picks. Different authors may arrive at the same final ratio by a slightly different counting breakdown, but the idea is consistent.)

Inclusion-exclusion principle

Generalizing further, we use the principle:

$$ P\Bigl(\bigcup_{i=1}^{8} A_i\Bigr)

;=;\sum_{i=1}^8 P(A_i) ;-;\sum_{i<j} P(A_i \cap A_j) ;+;\sum_{i<j<k} P(A_i \cap A_j \cap A_k) ;-;\dots $$

to account for overlapping events where multiple teams might simultaneously contain married couples.

Once we calculate those terms up to intersections of 8 events (though in practice many terms may become negligible or zero if they require “impossible” overlaps), we arrive at

P(A₁ ∪ A₂ ∪ ... ∪ A₈) ≈ 0.6553.

Therefore, the probability that no team contains a married couple is:

1 − 0.6553 = 0.3447.

Practical interpretation

Interpret this result as roughly a 34.47% chance that a random partition of 24 people (12 married couples) into eight teams of 3 will avoid placing any married couple together on the same team.

Potential Follow-up Questions

How do we know that all partitions into teams of three are equally likely?

We typically assume each of the C(24,3) ways to choose the first team, C(21,3) ways to choose the second team from the remaining 21 people, etc., is equally likely. More precisely, we consider all distinct ways of dividing the 24 individuals into 8 disjoint subsets of size 3 each. Mathematically, the total count of equally likely partitions (the multinomial way of grouping people into labeled teams) underpins the probability calculations.

What if the teams were unlabeled? Would that change the probability?

Yes. If the teams had no labels (i.e., all ways of splitting into sets of size 3 are considered the same if they contain the same subsets, regardless of order), you would use a different total count of ways to partition. However, for typical “Team 1, Team 2, …” labeling, we treat these teams as distinct. The same ratio for the final probability often remains the same in many symmetrical setups, but one must be consistent in how the denominator and numerator are counted.

Could we do a direct combinatorial count of “no couple on any team” without inclusion-exclusion?

Yes. One might try to count the number of ways to distribute each of the 12 couples to ensure no team includes both members. For instance, each couple has three choices of being placed: the two members must land in different teams or the same team. But we must ensure they never land in the same team, so effectively we want each pair to be placed in separate subsets of size 3. A direct approach can be complicated to manage carefully, because we must keep track of how many spots remain on each team, which leads to a more involved combinatorial argument. Inclusion-exclusion is a more systematic (though sometimes tedious) approach for these overlapping constraints.

Could we write a quick simulation in Python to estimate the probability?

Yes. For a large number of trials, we can randomly permute the 24 people, group them in sets of size 3, and check whether a married couple ends up in any team.

import math, random

def simulate_no_couples(num_sims=10_000_00):
    couples = [(i, i+12) for i in range(12)]  # example: (0,12), (1,13), ... to represent 12 couples
    count_no_couple = 0
    for _ in range(num_sims):
        people = list(range(24))
        random.shuffle(people)
        # Partition into 8 teams of 3
        teams = [people[i*3:(i+1)*3] for i in range(8)]

        # Check if any team has a married couple
        has_couple = False
        for t in teams:
            t_set = set(t)
            for c in couples:
                if c[0] in t_set and c[1] in t_set:
                    has_couple = True
                    break
            if has_couple:
                break

        if not has_couple:
            count_no_couple += 1

    return count_no_couple / num_sims

prob_est = simulate_no_couples()
print(prob_est)

Running a sufficiently large number of iterations will produce an estimate close to 0.3447.

Why might some inclusion-exclusion terms be zero at high order intersections?

When you try to force multiple teams to each contain a married couple, you eventually run out of couples or you have constraints that cannot all be satisfied simultaneously if too many teams are required to have distinct married couples. For example, to have all eight teams each contain a distinct married couple, we would need at least 8 distinct couples. But this is certainly possible if we have 12 total couples—so that term in the expansion wouldn’t necessarily be zero. However, if we had fewer couples than teams, a higher-order intersection event might become impossible, rendering it a zero term.

Are there other ways to see if the result is reasonable?

We know that once teams start forming, the chance that at least one team has a married couple increases significantly because there are many couples and only 3 slots per team. A resulting probability of around 65.53% for at least one team containing a couple is quite plausible, leaving about 34.47% for the complement.

Hence, the final answer that no team contains a married couple is approximately 0.3447.

Below are additional follow-up questions

What if the number of couples is different from 12? How does the approach generalize?

If there are fewer or more than 12 couples—for example, 10 or 15—one can still apply the same principle but must adjust the counts and probabilities accordingly. The main steps remain:

1. Define A_i as the event that team i contains at least one of the now N couples.

2. Use the same inclusion-exclusion principle to compute the probability of the union of the A_i events across all teams.

3. Recalculate the probabilities and intersection probabilities:

   • For P(A_i), choose which couple is on team i, then choose the extra person from the remaining pool.

   • For P(A_i ∩ A_j), account for the fact that after selecting a couple for team i, only N - 1 couples remain for team j, etc.

The complexity typically increases for more couples, because you have to handle more overlapping constraints in higher-order terms, but the principle remains identical. The final numeric result would certainly differ, reflecting the changed likelihood of couples ending up together.

A potential pitfall is forgetting that if you have fewer couples than the number of teams, certain higher-order intersection events (like all teams having couples) become impossible. Conversely, with more couples, the probability of forming at least one team with a couple generally increases, and none-of-the-teams-has-a-couple becomes less likely.

---

How can we extend this to different team sizes or a different number of teams?

If the team sizes are not 3, or if the number of teams is not 8, the combinatorial expressions adjust accordingly:

• For team size k, each team is chosen from 24 people as C(24, k), and the probability that a couple is on that team changes. Specifically, to have one married couple in a team of size k, you pick 1 of the N couples, then pick k - 2 additional individuals from the remaining 24 - 2 people.

• For a different number of total teams, say T, you would have T teams each of size k (with T·k = 24). Then define A₁, A₂, …, A_T to be “team i has at least one couple,” and apply inclusion-exclusion in the same manner with T terms.

A common pitfall is incorrectly assuming that the number of ways to partition 24 people remains the same or failing to modify the denominator to reflect the new partition structure. In principle, you simply carefully redo the counting arguments to reflect the new constraints.

---

Could this problem be approached using generating functions or other advanced combinatorial tools?

Yes, generating functions can sometimes handle partition problems by encoding ways of distributing couples across teams in polynomial expansions. One might construct a generating function in which each couple can be “placed” in different teams in ways that never allow both individuals in the same team. While possible, the approach can be intricate. Some steps would be:

• For each couple, assign them to different teams among T labeled teams.

• Track the number of ways to assign all couples and the leftover single individuals to fill team sizes exactly.

This can become quite complicated, but it can systematically produce the final count of valid partitions. For large T or more couples, the complexity might make direct generating functions impractical, although symbolic or computer algebra systems can sometimes handle these expansions.

One pitfall is incorrectly building or summing the polynomial terms in a way that either double counts or fails to account for constraints about total team sizes.

---

How would the probability change if some couples have different probabilities of showing up or if couples have variable chance to be “active” in the tournament?

If not all couples are guaranteed to participate—or if there is a probability p that a specific couple is “participating” in the sense that they must be kept apart—then we would move away from a uniform setup. One possible model:

1. Each couple is included in the final group with probability p, or equivalently, we might say each couple’s presence as a “constraint” is only with probability p.

2. Condition on the number of active couples in the final set. If X couples are active, revert to the same approach with X couples.

A key pitfall is that the event “couple is active” might not be independent across couples in real contexts. If the presence of one couple influences another’s attendance, you need more sophisticated conditional probability. As p→1, the problem reverts to the original. If p→0, the probability of no couples in any team trivially becomes 1 because there are essentially no constraints left.

---

What if we allow for multiple couples within the same team to matter? For example, we want no more than one couple in each team, but up to two or more couples could appear?

In our original problem, we simply want zero couples in a team. If we slightly relax the rule to “no more than one couple per team,” we then need to incorporate the possibility that a team might actually hold two couples if it has enough space (for instance, a team of 4 could theoretically include two couples). The probability question changes to:

• Define A_i as “Team i contains at least two couples.”

• We want 1 - P(A₁ ∪ … ∪ A_T).

But if the question is about bounding the number of couples per team to exactly one or zero, the logic of inclusion-exclusion can still be used, but the event definitions become more complex:

• A_i might be “Team i has 2 or more couples.”

• A_i ∩ A_j is “Team i has 2+ couples AND team j has 2+ couples,” and so on.

A subtlety is verifying that a single team can actually hold 2 or more couples given its size. For instance, with teams of 3, you cannot have 2 distinct couples in the same team, so that event is automatically impossible. Therefore, the details really hinge on team size as well as the constraints placed on the couples.

---

How can real-world constraints (e.g., skill levels, geographical limitations, etc.) alter this probability model?

In practice, forming teams might involve constraints beyond purely random grouping:

• Skill balancing: Organizers might try to avoid placing two very strong or very weak players together, affecting the random distribution. If a couple has correlated skill levels, they might be more or less likely to be placed together.

• Geographical or scheduling restrictions: Some couples might only be able to play in certain time slots, restricting how the partition is formed.

These constraints effectively break the assumption of every partition being equally likely. To adapt the probability model, one would need to account for weighting factors that measure the relative likelihood of each partition under the new constraints. A typical pitfall is to apply the uniform probability model ignoring these real-world biases, leading to an incorrect estimate.

---

In an actual event planning scenario, would we rely solely on this theoretical probability?

Not necessarily. While the theoretical model provides a baseline understanding of how couples might randomly be placed into teams, many events:

• Manually intervene to ensure couples are not on the same team if that’s desirable.

• May conduct a random draw but then do a quick check or swap to avoid couples together.

The theoretical probability is valuable for a purely random assignment. Once manual adjustments enter the scene, the distribution of final team compositions can differ. A major practical pitfall is to trust the theoretical probability while ignoring the fact that organizers might intentionally alter teams to satisfy certain preferences, making the real-world outcome deviate significantly from the theoretical result.