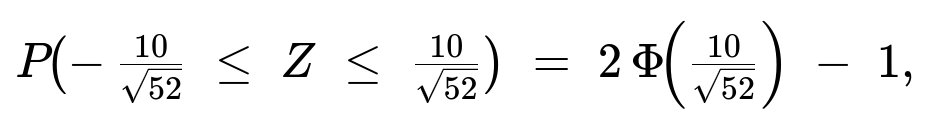ML Interview Q Series: Calculating Probability of Average Measurement Accuracy Using Normal Distribution.
Browse all the Probability Interview Questions here.
Two instruments are used to measure the unknown length of a beam. If the true length of the beam is l, the measurement error made by the first instrument is normally distributed with mean 0 and standard deviation 0.006l, and the measurement error made by the second instrument is normally distributed with mean 0 and standard deviation 0.004l. The two measurement errors are independent of each other. What is the probability that the average value of the two measurements is within 0.5% of the actual length of the beam?
Short Compact solution
Since the random variables X1 and X2 (the measurement errors) are independent and normally distributed with mean 0 and standard deviations 0.006l and 0.004l respectively, the random variable (1/2)(X1 + X2) is also normally distributed with mean 0 and standard deviation
We want the probability
Equivalently, this is
P( |(X1+X2)/2| <= 0.005 l ) = P( |X1+X2| <= 0.01 l ).
Standardizing by the standard deviation of (1/2)(X1 + X2) leads to
where Z is a standard normal random variable and Φ denotes the standard normal CDF. Numerical evaluation gives approximately 0.8345.
Comprehensive Explanation
Distribution of Individual Measurement Errors
Each measurement error X1 and X2 is assumed to be normally distributed around 0 but with different scales proportional to l:
X1 ~ Normal(0, (0.006l)²)
X2 ~ Normal(0, (0.004l)²)
These reflect the error variability from each instrument relative to the true length of the beam.
Distribution of the Average Measurement
We define the average of the two instrument readings (in terms of error) as Y = (X1 + X2)/2. Since X1 and X2 are independent normals, their sum X1 + X2 is also normal with:
Mean 0 (since each has mean 0)
Variance = (0.006l)² + (0.004l)²
Hence,
The standard deviation of (X1 + X2) is sqrt((0.006l)² + (0.004l)²).
The random variable Y = (X1 + X2)/2 then has its variance scaled by (1/2)². Therefore, std(Y) = (1/2) * sqrt((0.006l)² + (0.004l)²).
Event of Interest
We need the probability that the average measurement is within 0.5% of l, meaning:
(1/2)|X1 + X2| <= 0.005 l
Equivalently,
|X1 + X2| <= 0.01 l.
Standardizing
Define Y = (X1 + X2)/2. Then Y is normal(0, (std(Y))²). Its standard deviation is
(1/2)*sqrt((0.006l)² + (0.004l)²) = (l / 2000)*sqrt(52).
The event |Y| <= 0.005 l translates to
|Y| / [ (l / 2000)*sqrt(52 ) ] <= 0.005 l / [ (l / 2000)*sqrt(52 ) ].
Simplifying the right-hand side:
0.005 l / [ (l / 2000)*sqrt(52 ) ] = 0.005 l * (2000 / l) / sqrt(52 ) = (0.005 * 2000) / sqrt(52 ) = 10 / sqrt(52 ).
Thus,
P( |Y| <= 0.005 l ) = P( -10/sqrt(52 ) <= Z <= 10/sqrt(52 ) ),
where Z is standard normal. Therefore, the probability is
2 Φ(10/sqrt(52 )) - 1 ≈ 0.8345.
Potential Follow-Up Questions
1) Why do we directly add the variances of X1 and X2?
Because X1 and X2 are independent normal random variables, the variance of their sum is the sum of their variances. If they were correlated, we would have to include covariance terms. But independence implies zero covariance, so we simply add (0.006l)² and (0.004l)² to get the variance of X1+X2.
2) What if the errors were correlated?
In that case, the variance of (X1+X2) would be Var(X1) + Var(X2) + 2 Cov(X1, X2). Cov(X1, X2) would need to be incorporated based on the correlation coefficient ρ. The standard deviation of the sum would then be sqrt((0.006l)² + (0.004l)² + 2ρ(0.006l)(0.004l)). This would change the probability calculation since the distribution’s variance would differ.
3) Could we use Chebyshev’s inequality or other bounds for this calculation?
Yes, in principle. Chebyshev’s inequality or Hoeffding’s inequality can give general bounds on probabilities for random variables, but these bounds can be quite loose compared to the exact normal calculation. Since the question states normal errors explicitly, using the normal distribution is both accurate and straightforward.
4) How might sampling many measurements affect the result?
If you have more than two instruments (or multiple measurements from each instrument) and average all of them, the standard deviation of that average typically decreases. For n independent measurements each with its own variance, the average’s variance would be the sum of all those variances divided by n². As n grows, the distribution of the average measurement tightens, leading to higher probability of being within a certain tolerance.
5) Why is the probability relatively high (~83%) instead of near 50% or 99%?
The standard deviations 0.006l and 0.004l are not extremely large relative to 0.5% of l. Combining them and then halving the sum (since we are taking an average) creates a smaller net standard deviation compared to 0.5% of l, which yields a fairly high coverage probability of about 83%.
6) How to implement this in Python for a quick check?
Below is a simple Python snippet that uses scipy.stats.norm to approximate the probability numerically:
import numpy as np
from scipy.stats import norm
std_sum = np.sqrt((0.006)**2 + (0.004)**2) # std of X1 + X2 in units of l
std_avg = 0.5 * std_sum # std of (X1 + X2)/2
tolerance = 0.005 # 0.5%
# Convert the event (|Y| <= 0.005 l) into a Z range
z_bound = tolerance / std_avg
prob = 2 * norm.cdf(z_bound) - 1
print(prob)
This should yield a numerical value close to 0.8345.
Below are additional follow-up questions
What if the error distributions are not normal?
If the error distributions deviate significantly from normal (for example, if they are skewed, multimodal, or heavy-tailed), the assumptions behind summing variances and using the standard normal distribution for Y = (X1 + X2)/2 may no longer hold. In such cases, you cannot rely on the exact standard normal probabilities, and you may need to:
Use non-parametric methods or simulations (e.g., bootstrap) to estimate the probability of |Y| <= 0.005 l.
If you have reason to believe the errors might be heavy-tailed (e.g., Cauchy-like distributions), you would see significantly larger variance contributions from outliers, and even moments like variance might not be well-defined. You might have to rely on robust statistical methods or bounding techniques like Chebyshev or Cantelli inequalities.
Check empirical data from the instruments to see if normal is a good fit. If it is not, you might try other flexible distributions (like Student’s t) that can model heavier tails.
A key pitfall is blindly assuming normality just because “many processes are normal.” Real measurement devices might generate outliers due to random sensor glitches, so you must validate normality assumptions first.
How do we handle the possibility of outliers or gross errors in measurements?
If outliers occur with non-negligible frequency, they can significantly distort the mean and inflate the variance. In practice, outliers might come from:
Instrument malfunctions or calibration issues.
Environmental interference (e.g., temperature spikes or vibrations).
Data entry or transcription errors.
A few approaches to manage outliers in calculating the probability of being within 0.5% of l include:
Use robust estimators of central tendency (e.g., median) instead of the mean if the distribution is grossly contaminated by outliers.
Apply robust methods (e.g., M-estimators, trimming, or winsorizing) to reduce the impact of extreme values.
Model outliers explicitly: for instance, suppose 95% of errors follow a normal distribution and 5% come from a heavier-tailed process. Then compute the blended probability distribution for (X1 + X2)/2 accordingly.
Pitfall: If an outlier is real (e.g., a truly faulty measurement) and you simply ignore it, your estimate of probabilities may be biased. Conversely, if you incorporate these outliers without distinguishing them from nominal measurements, you might end up with an overly pessimistic or inaccurate probability.
How can one validate that the standard deviations 0.006l and 0.004l are correct?
You typically estimate these values by analyzing historical measurement data or by running calibration experiments. For each instrument:
Measure a known standard length multiple times under consistent conditions.
Compute sample standard deviations from the repeated measurements.
Compare these sample standard deviations to the stated 0.006l and 0.004l. If the observed stats deviate substantially, you may need to adjust your model.
In practice:
Ensure that the test conditions match real-world operating conditions (temperature, humidity, operational load).
Check for drift over time: the standard deviation might be stable initially but could change if the instrument ages or if there are mechanical wear-and-tear issues.
Periodically re-calibrate and re-estimate these values for ongoing accuracy.
Pitfall: If the environment changes (e.g., measuring in drastically different temperatures or altitudes), these standard deviations may no longer represent the real error behavior.
How to interpret this probability for measurements taken over extended periods or varying conditions?
Real-world measurements do not always happen under identical conditions. Over time, instrument biases might shift, or the environment (temperature, humidity, vibrations) might induce extra variability. This means:
The assumption of a fixed standard deviation 0.006l and 0.004l could be inaccurate if conditions vary significantly.
You may need a hierarchical or mixed-effects model that accounts for day-to-day or session-to-session variability in measurement.
If you use a single normal distribution with a fixed standard deviation, you might underestimate or overestimate the tail probability of large errors, especially if the real measurement process systematically changes over time.
A possible pitfall is ignoring time-dependent effects and continuing to assume a single “global” normal distribution. You could gather data from different time windows and confirm that the distribution remains stable. If not, incorporate a model that captures time-varying or seasonal components.
What if we used only one instrument multiple times instead of two different instruments?
In that scenario, you might want to compute the average of multiple measurements from the same instrument. Suppose you collect n independent measurements from that one instrument with standard deviation 0.006l. Then the standard deviation of their average would be 0.006l / sqrt(n). So, the probability that this average is within 0.005l of the true length depends on n:
As n grows, the standard deviation of the average shrinks, increasing the probability of being within 0.5% of l.
However, if the instrument introduces consistent bias or correlated errors over time, simply averaging more readings might not help as much. You need to ensure independence or at least quantify correlation.
Pitfall: If the single instrument has a systematic bias, taking multiple measurements and averaging them does not eliminate the bias; it just reduces random fluctuation.
How many total measurements might be needed to achieve a specific confidence (e.g., 99%) that the average is within 0.5% of l?
To achieve a higher probability (like 99%) you can:
Combine more instruments (each with its own known standard deviation).
Take repeated measurements from each instrument.
Derive the variance of the combined average.
If you have n1 measurements from the first instrument and n2 from the second, each measurement from instrument 1 has variance (0.006l)², and from instrument 2 has variance (0.004l)². If you average them properly (a weighted average, if needed), the resulting standard deviation will shrink with increasing n1 and n2. You would then standardize the event “the combined average is within 0.005l” by the new standard deviation.
Formally, if all measurements are independent, you might compute:
For instrument 1: variance per measurement = (0.006l)², so variance of the mean of n1 measurements = (0.006l)² / n1.
Similarly for instrument 2: variance per measurement = (0.004l)², so variance of the mean of n2 measurements = (0.004l)² / n2.
If you average the two means, you would get a combined variance that accounts for the weights used.
The goal is to pick n1 and n2 so that the probability of the combined average being within 0.005l is at least 0.99. You then solve for n1 and n2 by standard normal approximations or iterative search.
Pitfall: Overestimating how quickly your confidence grows with more measurements if there are hidden correlations or if the real distribution is not normal. In the real world, you might see diminishing returns if the process changes over time.
What if the instrument calibrations or the true length l can change over time?
If l itself is not truly fixed (for example, a beam might expand or contract with temperature), or if the instrument’s calibration drifts, the entire assumption that the error distributions revolve around a constant “true length” might be invalid. You might need to:
Treat l as a random variable itself with its own uncertainty distribution.
Simultaneously model the instrument drift as an unknown, time-varying bias.
Use dynamic calibration protocols that track the instrument’s offset from known reference objects periodically.
Pitfall: If you continue to assume a fixed true length in the face of actual length changes, your “within 0.5%” probability can be misleading, as part of the variability you see could be from l changing, not just from measurement noise.
Could we incorporate Bayesian updating if we have prior beliefs about instruments’ biases or uncertainties?
Yes. A Bayesian approach lets you encode prior distributions over unknown parameters, such as:
The mean bias of each instrument.
The standard deviations of their errors.
You then update these priors with observed data (multiple measurements of known standards or repeated measurements of the beam) to obtain posterior distributions. The probability of “the average being within 0.5% of l” can then be computed by integrating over the posterior. Specifically, you might:
Specify prior distributions for the bias and standard deviations (e.g., inverse-gamma for variances, normal for biases).
Collect measurements of the beam or a calibration standard.
Use Bayesian inference (MCMC or variational methods) to obtain the posterior distribution of the combined average error.
Compute the posterior predictive probability that the average measurement is within 0.5% of l.
Pitfall: A Bayesian approach can be computationally more expensive and requires you to choose priors carefully. Overly wide or narrow priors can distort your posterior in ways that might not align with reality, so you have to ensure your prior beliefs are justified by historical data or domain knowledge.