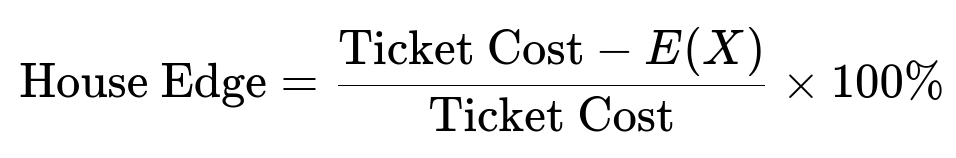ML Interview Q Series: Calculating Expected Value and House Edge for a Four-Digit Lottery
Browse all the Probability Interview Questions here.
A four-digit number is chosen uniformly at random from the range 0000 to 9999. A lottery ticket costs $2. You win $50 if your ticket matches the last two digits (but not the last three), $500 if your ticket matches the last three digits (but not all four), and $5,000 if your ticket matches all four digits. What is the expected payoff on a lottery ticket? What is the house edge of the lottery?
A four-digit number is chosen uniformly at random from the range 0000 to 9999. A lottery ticket costs $2. You win $50 if your ticket matches the last two digits (but not the last three), $500 if your ticket matches the last three digits (but not all four), and $5,000 if your ticket matches all four digits. What is the expected payoff on a lottery ticket? What is the house edge of the lottery?
Short Compact solution
The probability of winning $50 by matching only the last two digits (and not the last three) is 9/1000. The probability of winning $500 by matching only the last three digits (and not all four) is 9/10000. The probability of winning $5,000 by matching all four digits is 1/10000. The probability of winning nothing is 99/100.
Thus the expected payoff is 0*(99/100) + 50*(9/1000) + 500*(9/10000) + 5000*(1/10000) = 1.4 (in dollars). Since the ticket costs $2, the house edge is ((2 - 1.4) / 2) * 100% = 30%.
Comprehensive Explanation
Key idea of expected value
The expected payoff of a random variable can be found by summing over all possible outcomes multiplied by their respective probabilities. Here, the random variable X is the payoff (in dollars) of your lottery ticket (not yet accounting for the ticket cost). Once you account for the ticket price, you can determine whether this lottery has a positive or negative expectation for the player.
Core expected value formula
where x_{i} is the payoff amount for each possible outcome i, and p_{i} is the probability of that outcome.
Breaking down each outcome
There are 10,000 possible 4-digit numbers from 0000 to 9999.
Matching all four digits occurs with probability 1/10000. The payoff is $5,000.
Matching only the last three digits (but not all four) can occur in 9 out of the 10 possibilities for the first digit. Hence the probability is 9/10000. The payoff is $500.
Matching only the last two digits (but not the last three) can occur in 9 out of the 100 possibilities for the first two digits. Hence the probability is 9/1000. The payoff is $50.
In all other cases, the payoff is $0.
Hence, numerically:
P(X=0) = 99/100
P(X=50) = 9/1000
P(X=500) = 9/10000
P(X=5000) = 1/10000
Expected payoff calculation
Multiply each payoff by its probability and sum:
0 * (99/100)
50 * (9/1000)
500 * (9/10000)
5000 * (1/10000) = 1.4 dollars.
Accounting for ticket cost
You pay $2 for the ticket. The net expectation for the player is 1.4 - 2 = -0.6, meaning you lose $0.60 on average per ticket you buy.
House edge
The house edge is the percentage of the ticket price that you lose on average. In other words, how much the lottery (the “house”) keeps in expectation. Formally:
Here the ticket cost is $2 and E(X) is $1.4. So the house edge is:
((2 - 1.4) / 2) * 100% = 30%.
This 30% figure indicates that for every $2 ticket purchased, the lottery (on average) retains $0.60, which is 30% of the $2 initial cost.
Follow-Up Question: Relationship Between “Payoff” and “Profit”
How do we distinguish between the “expected payoff” versus the “expected profit” or “expected net return” in a lottery context?
When calculating the expected payoff, we ignore the initial cost of the ticket. This is simply the amount you receive (0, 50, 500, or 5000) multiplied by the respective probabilities. However, once you factor in the cost of the ticket (which is always $2 regardless of the outcome), the value that matters to a gambler is the expected net gain (or loss), which is expected payoff - cost of ticket.
In this lottery:
The expected payoff is $1.4.
The cost of the ticket is $2.
The expected net return = $1.4 - $2 = -$0.6.
This negative net expectation explains why the lottery is typically in favor of the house.
Follow-Up Question: How Would This Change If the Payouts Were Adjusted?
If the payouts for matching certain digits were changed, the overall probabilities remain the same because they are determined by how many digits match. But with different payout amounts, your new expected payoff would be computed in the same way: multiply each new payoff by the original probability for that outcome and sum them up, then subtract the cost of the ticket to find the net expectation. If that net expectation is still negative, the house edge remains in favor of the lottery.
Follow-Up Question: Practical Considerations for Real Lotteries
In many real-world lotteries:
Additional rules may apply, such as multiple ways to play each ticket (box play, straight play, etc.).
Administrative fees or taxes can further reduce the effective return.
Lotteries often distribute promotional prizes to maintain player interest, but these usually do not eliminate the house edge.
From a probabilistic viewpoint, the approach to determine expected values remains exactly the same. You identify the possible outcomes, compute their probabilities, and multiply each outcome’s payoff by its probability. The difference lies purely in what payoff structure is advertised by the lottery operator.
These considerations underscore the broader principle that, in nearly all lotteries, the expected return is negative for players, ensuring a built-in profit margin (house edge) for the operator.
Below are additional follow-up questions
What if the lottery allowed partial refunds or “buy-back” of tickets before the draw?
One scenario to consider is if the lottery offers a partial refund of the ticket price before the winning numbers are announced. For example, imagine you buy a $2 ticket, but at some point before the draw you can sell your ticket back to the lottery for $1. In theory, you could model the ticket at that time as a random variable with some expected value. However, unless there is new information about the draw or about how many other people are purchasing tickets, the expected value remains the same. In practice:
If the partial refund is higher than the expected net value of the ticket at that moment, a rational player might choose to accept the buy-back.
Conversely, if the partial refund is lower than the expected net value (which is typically $1.4 in payoff, minus the $2 cost), then a rational player would hold onto the ticket.
The critical point is the same expected value computation underlies decisions about buy-back or holding, since the probabilities of each outcome do not change just because buy-back is offered. A subtle pitfall is if a player incorrectly accounts for sunk cost: they might either undervalue or overvalue the opportunity to sell back their ticket, mixing emotional or non-rational decision factors.
How do risk aversion or utility functions change the desirability of the lottery?
Classical expected value calculations assume a linear utility for money (i.e., winning $5,000 has exactly 100 times the “utility” of winning $50). However, many real individuals exhibit risk-averse behavior, which can be captured by a concave utility function u(x). For example, a common form is a logarithmic utility: u(x) = ln(x). Under risk-averse preferences, large but rare jackpots might be valued less than their raw dollar amounts suggest, because the gain in utility from $5,000 might not be 100 times the gain in utility from $50.
Such a person would place a lower “personal value” on the $5,000 prize compared to someone with linear utility. Consequently, the lottery may be even less appealing than the negative expected value calculation suggests. The same approach applies to risk-seeking or risk-neutral players, but the shape of the utility function directly impacts how they perceive the lottery’s attractiveness. A key pitfall is ignoring personal utility altogether and focusing only on raw monetary expectation, especially if the participant is extremely risk-averse or risk-seeking.
How would you calculate the variance and standard deviation of the payoff?
The variance of a random variable X quantifies the spread of its possible values around the mean. Once you have computed the expected value E(X), you can compute E(X^2), the expectation of the square of the payoff, and then use:
Variance(X) = E(X^2) - [E(X)]^2 Standard Deviation(X) = sqrt(Variance(X))
In this lottery:
X can take values 0, 50, 500, and 5,000, with probabilities 99/100, 9/1000, 9/10000, and 1/10000 respectively.
You would calculate E(X^2) = sum over i of [ x_i^2 * p_i ].
This variance might be quite large because 5,000 is far from the mean of 1.4. A subtlety is that for a single play, variance alone may not feel very intuitive—players might care about downside risk. But for repeated plays, the variance heavily influences the possible range of cumulative outcomes. The pitfall here is failing to realize that, although the average net is -$0.60 per ticket, you might go on an extended “lucky streak” or “unlucky streak,” making short-term outcomes quite volatile.
What if you repeatedly play the lottery a large number of times?
By the Law of Large Numbers, if you keep playing the lottery many times independently, your average winnings per ticket will converge to the expected payoff (which is $1.4 per ticket in payoff, or -$0.60 net if we include the $2 cost). Over many trials:
Total amount spent ~ number_of_tickets * $2
Total amount won ~ number_of_tickets * $1.4
Net result ~ number_of_tickets * (1.4 - 2) = -0.6 * number_of_tickets
Thus, over the long run, you would expect to lose $0.60 for every ticket purchased, and your total loss would grow proportionally with the number of tickets you buy. A subtle pitfall is thinking short-term luck might turn the negative-expectation lottery into a profitable endeavor permanently. While you can experience variance in smaller samples, the house edge eventually dominates.
What if there is a cap on the total payout or an alteration in the distribution of prizes once certain thresholds are met?
Some lotteries may impose caps or recalculate payouts if too many people win in a single draw. For instance, if multiple tickets match all four digits, the $5,000 prize might be split among the winners. This changes the distribution of possible outcomes for each ticket, complicating the expected value calculation because your probability of receiving the full $5,000 depends on the number of other winning tickets.
In that scenario, the payoff for matching four digits is not necessarily 5,000 but 5,000 / (number of all-four-digit winners). In expectation terms, you would need to incorporate the probability distribution of how many total tickets match (which depends on how many people buy tickets and how correlated their chosen numbers are). A pitfall is to use 5,000 as a fixed payoff if it is actually subject to splitting.
How do changes in the total number of participants or correlation among chosen ticket numbers affect your individual expected payoff?
In an ideal scenario with a uniform and independent draw of the winning number, your individual ticket has a fixed probability distribution as we calculated (1/10,000 for matching all digits, etc.). However, if the number of participants is extremely large and many players pick the same numbers (perhaps due to “lucky number” bias or date-based choices), that can affect the portion of the prize you eventually share in certain payout structures. If the lottery does not require sharing the jackpot among multiple winners, your expected value remains the same. If the jackpot must be shared among all winners of that outcome, your effective payoff is less than 5,000 whenever multiple winners occur.
A subtlety is that your probability of winning or the payoff upon winning might shift based on how other players pick their numbers. In practice, for a standard pick-any-4-digit lottery with uniform random draws, the correlation effect among participants is usually small unless there is a known pattern. Nevertheless, in some specialized lotteries or scenarios, it is a real concern.
Could you ever make this lottery a positive-expectation bet if additional promotions or overlays were introduced?
In rare cases, lotteries or betting games introduce promotions such that the sum of expected winnings exceeds the cost of tickets. For instance, if the operator added a guaranteed bonus prize, or a situation known as an “overlay” occurred where the guaranteed payout is higher than the total money spent by participants, then the expected value of a ticket could become positive.
For example, if an extra $10,000 prize were added to a random participant, or if tickets were partially subsidized by another entity, you might push the expected net outcome above zero. The pitfall is to assume standard lottery structures have such overlays. Generally, governments and private operators design lotteries to have a house edge, so an overlay is rare and usually short-lived.
How might taxes or additional fees alter the final expected net return?
In many jurisdictions, lottery winnings are taxed. If your winnings are subject to, say, a 25% tax on gambling income, then the after-tax payoffs are effectively smaller:
$50 becomes $37.50 after 25% tax,
$500 becomes $375,
$5,000 becomes $3,750.
Recalculating the expected payoff using after-tax amounts typically lowers it significantly. Because the ticket cost ($2) is not usually tax-deductible for these purposes (in many jurisdictions), the net expected return to the player is even more negative. One subtlety is that some smaller prizes might be below a certain threshold and not taxed, or local regulations differ, so you have to be precise about how tax rules apply. A big pitfall is to overlook taxes, which further disadvantages the player beyond the raw house edge calculation.
Why might players engage in lotteries despite a negative expected value?
While not strictly a mathematical question, behavioral and psychological factors can lead people to purchase lottery tickets even when the expectation is negative. Examples include:
The thrill of a potential large windfall,
Overestimation of small probabilities (a known bias in decision theory),
Social factors (peer influence, office lottery pools),
Mistaken beliefs or superstitions regarding the likelihood of winning.
From a pure mathematics standpoint, the negative expectation indicates the house advantage. However, humans are not purely rational utility optimizers. A pitfall is to analyze lotteries only via expected monetary values and ignore that people might find entertainment value or emotional satisfaction worth the cost of the ticket.
How does the Central Limit Theorem apply to repeated lottery outcomes?
If you buy a large number of tickets independently (each with the same distribution of payoffs), then by the Central Limit Theorem, your total winnings (minus your total costs) will be approximately normally distributed around the mean (the sum of each ticket’s expected net). Specifically:
Mean of total winnings = (number_of_tickets) * E(X).
Variance of total winnings = (number_of_tickets) * Var(X) (assuming independence).
As the number_of_tickets grows large, the distribution of the total payoff tends to be bell-shaped around that mean. A potential pitfall is applying the Central Limit Theorem to extremely small sample sizes or ignoring correlation between tickets (for example, if some partial matching rules are based on digits and you intentionally pick correlated numbers). In standard lottery scenarios, each draw is typically independent, and if each ticket is a separate draw, the normal approximation should be reasonable for large numbers of trials.