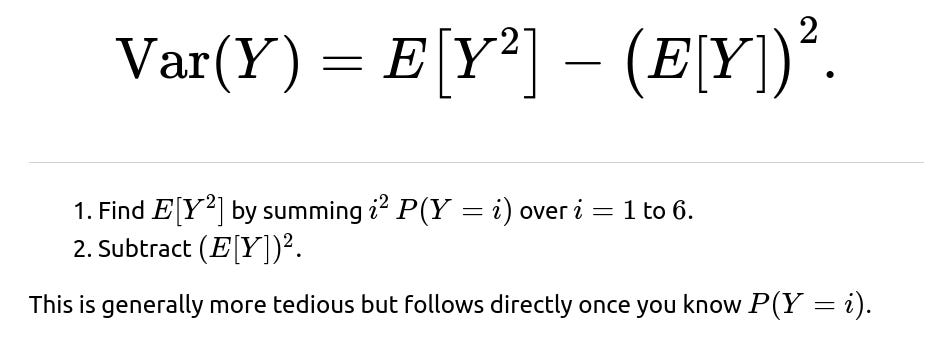ML Interview Q Series: Calculating the Expected Maximum Value of Two Dice Rolls Using Probability.
Browse all the Probability Interview Questions here.
If two standard six-sided dice are rolled, what is the expected value of the higher of the two rolls?
Short Compact solution
The probability that Y equals some value i because the first die is i and the second is less than i.
The probability that Y equals i because the second die is i and the first is less than i.
The probability that both dice show i simultaneously.
For a particular i:
Probability that the first die is i while the second is strictly less is (1/6)×((i−1)/6).
The same probability applies for the second die being i while the first is less.
The probability that both dice are i is (1/6)×(1/6).
Summing everything from i=1 to i=6 and multiplying by i gives:
Hence, the expected maximum of two dice is 161/36, which is around 4.47.
Reasoning Behind the Probability Computation
Possible values of YY can be 1, 2, 3, 4, 5, or 6 because it is defined as the maximum of two rolls.
Computing P(Y=i) We want to find the chance that the maximum is exactly i. This event happens if:
Either the first die is i, the second die is less than i.
Or the second die is i, the first die is less than i.
Or both dice are i.
Combining these probabilities The total probability that Y=i is:
5. Expected value calculation The expected value of Y is given by summing over all possible i (from 1 to 6), multiplied by P(Y=i):
Potential Follow-up Question 1: Why does this approach work and could we use a contingency table to confirm?
Key Points:
Each cell is equally likely with probability 1/36.
By adding the maximum values in each cell, you get the total sum of maxima over all possible outcomes.
Divide that sum by 36 (the total number of equally likely outcomes) to obtain E[Y].
Potential Follow-up Question 2: How can we extend this to n dice instead of just 2?
Potential Follow-up Question 3: Could we compute the variance of the maximum?
Yes, once you know the distribution of Y, you can compute:
Potential Follow-up Question 4: How to implement a quick simulation in Python to verify?
We can run a Monte Carlo simulation to empirically estimate the expected value of the maximum of two dice. For instance:
import random
import statistics
def simulate_max_of_two_dice(num_simulations=10_000_000):
max_values = []
for _ in range(num_simulations):
roll1 = random.randint(1, 6)
roll2 = random.randint(1, 6)
max_values.append(max(roll1, roll2))
return statistics.mean(max_values)
if __name__ == "__main__":
est_value = simulate_max_of_two_dice()
print(f"Estimated expected maximum (two dice) after simulation: {est_value}")
We run many trials, rolling two dice at a time, record the maximum each time, and then average the results.
As we increase the number of simulations, the empirical average will converge near 4.47, confirming our analytical result.
Potential Follow-up Question 5: What pitfalls might occur in practice?
Miscounting Outcomes: When people try to do this by enumerating pairs, they can forget that there are 36 outcomes in total or fail to include scenarios where both dice are the same.
Mixing Up Distributions: Sometimes it is confused with the distribution of the sum of the dice. The sum’s expected value is 7, but the maximum is about 4.47.
Computational Precision: If you simulate with too few iterations, your estimate might be off from the true 4.47 because of random fluctuations.
Each of these pitfalls highlights why a careful mathematical derivation or a sufficiently large simulation is essential to confirm the correct result.
Below are additional follow-up questions
How would the answer change if the dice were biased instead of fair?
The probability that the first die lands on i and the second die lands on a value less than i.
The probability that the second die lands on i and the first die lands on a value less than i.
The probability that both dice land on i.
In mathematical terms,
How do we generalize the result if the dice do not have 6 sides?
If we only care about the maximum when it exceeds a certain threshold, how can we compute the conditional expectation?
How would partial information about one die roll affect the probability distribution of the maximum?
How do we determine the median or other quantiles of the maximum distribution?
Is there a direct combinatorial argument for finding P(Y=i) without enumerating all pairs?
How do we handle a situation where the dice have non-integer faces or custom labels?
How do you reason about the maximum if we roll multiple times under certain conditions or rules?
In many real-world board games, you might roll two dice but get to re-roll under certain conditions, such as if they tie, or if the maximum is below a certain threshold. This effectively changes the distribution of Y. You would need to treat it as a multi-step stochastic process:
Roll the dice once and observe Y.
If Y meets some re-roll condition (for example, Y<3), you roll again.
Possibly repeat or stop based on additional constraints.
In each roll, you compute the probability of each possible Y value. Then you incorporate the re-roll rule to find the probability distribution of Y at each step. Eventually, you solve for the long-run or final distribution of Y. A subtlety is that repeated rolling can create a Markov chain with states representing the possible outcomes of Y or the dice. Handling the probability transitions systematically is crucial to avoiding miscalculation. Another subtlety is that each re-roll might not be independent of the previous result if the rules condition on certain events like a tie.