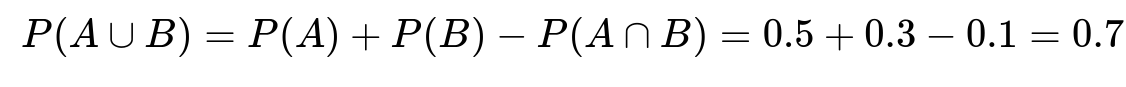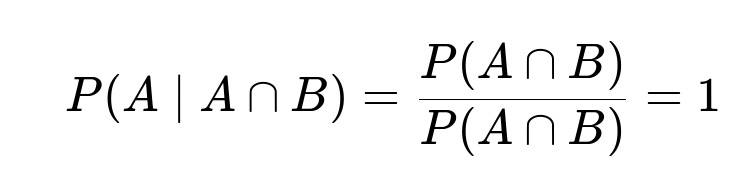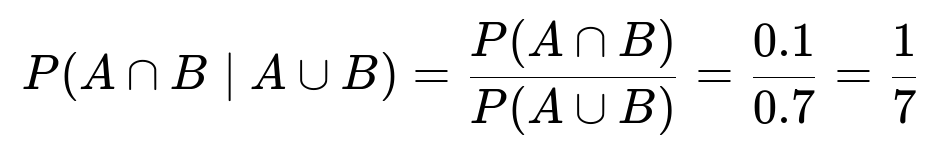ML Interview Q Series: Calculating Various Conditional Probabilities Using Basic Probability Rules
Browse all the Probability Interview Questions here.
Two events A and B are such that P(A)=0.5, P(B)=0.3 and P(A∩B)=0.1. Calculate:
(a) P(A|B) (b) P(B|A) (c) P(A|A∪B) (d) P(A|A∩B) (e) P(A∩B|A∪B)
Short Compact solution
P(A|B)
To find P(A|A∪B), note that:
Hence,
P(A|A∩B)
P(A∩B|A∪B)
Comprehensive Explanation
Overview of Conditional Probability
Conditional probability captures the likelihood of one event occurring given that another event has already happened. Formally, for two events X and Y with nonzero probability P(Y) > 0, the conditional probability P(X|Y) is defined as the ratio of the joint probability P(X ∩ Y) to P(Y). This concept is crucial when events do not occur independently and we want to understand how the occurrence of one event informs us about the occurrence of another.
Reasoning Through Each Calculation
1. P(A|B)
This is asking: “Given that event B has occurred, what is the probability that event A has also occurred?” We know:
P(A ∩ B) = 0.1
P(B) = 0.3
So we directly apply the conditional probability formula:
P(A|B) = P(A ∩ B) / P(B) = 0.1 / 0.3 = 1/3.
Intuitively, out of all the outcomes in which B happens, one-third of those outcomes also have A happening.
2. P(B|A)
This is the probability that B occurs given that A is known to have occurred. Again, we use:
P(B|A) = P(A ∩ B) / P(A) = 0.1 / 0.5 = 1/5.
This means that among all outcomes where A happens, only one-fifth of them also include B.
3. P(A|A ∪ B)
First, we compute the probability of the union, A ∪ B:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B) = 0.5 + 0.3 - 0.1 = 0.7.
The conditional probability P(A|A ∪ B) then is:
P(A|A ∪ B) = P(A) / P(A ∪ B) = 0.5 / 0.7 = 5/7.
Interpretation: once you know that “either A or B (or both) has occurred,” the chance it was specifically A is 5/7.
4. P(A|A ∩ B)
Here, we condition on A ∩ B, which means we already know that both A and B occurred. If both have already occurred, the event “A occurred” is certain in that subset of outcomes. Formally,
P(A|A ∩ B) = P(A ∩ B) / P(A ∩ B) = 1.
This is a common situation in probability: conditioning on the intersection of events that already includes A means A is guaranteed.
5. P(A ∩ B|A ∪ B)
This measures how likely the intersection A ∩ B is, given that at least one of A or B has happened. We use the ratio:
P(A ∩ B|A ∪ B) = P(A ∩ B) / P(A ∪ B) = 0.1 / 0.7 = 1/7.
So, out of all scenarios where either A or B (or both) occurs, only 1/7 of those scenarios are the ones where both A and B happen together.
Why These Formulas Work
The key formula for conditional probability is always P(X|Y) = P(X ∩ Y) / P(Y).
For the union, the standard inclusion-exclusion formula P(A ∪ B) = P(A) + P(B) - P(A ∩ B) is used.
When we condition on an event that strictly implies another (like A ∩ B implies A), the conditional probability must be 1.
Practical Example Interpretation
Imagine A is “user clicked on an ad” and B is “user saw the ad in a recommended list.” Then:
P(A|B) = 1/3 means whenever the user sees the ad, they click on it 33% of the time.
P(B|A) = 1/5 means if a user clicked on an ad, only 20% of the time it was one from the recommended list.
P(A|A ∪ B) = 5/7 means if we know the user either clicked or it appeared in the recommended list, the proportion of times it was a click event alone is about 71.4%.
P(A|A ∩ B) = 1 means that if an event is “the user saw the ad in the recommended list and clicked on it,” obviously the user clicked (event A).
P(A ∩ B|A ∪ B) = 1/7 means only 14.3% of the time, among all “saw or clicked” scenarios, do we see the user actually both see and click.
Potential Follow-up Questions
What is the difference between P(A|B) and P(B|A)?
P(A|B) is the probability that A occurs given that B has occurred. P(B|A) reverses that perspective: it is the probability that B occurs given A has occurred. Because these two probabilities are typically not equal (unless A and B have certain special relationships like symmetry or independence), one must always be careful about the direction of conditioning.
In our example, P(A|B) = 1/3 while P(B|A) = 1/5, reflecting that these two relationships have different likelihoods.
Why is P(A|A ∩ B) = 1?
When you condition on A ∩ B, you are restricting your sample space exclusively to outcomes where A and B both happen simultaneously. Within that restricted sample space, A has already occurred by definition. Thus, P(A|A ∩ B) must be 1 because there is no scenario in A ∩ B where A does not happen.
What happens if P(B) = 0 when computing P(A|B)?
If P(B) = 0, the expression P(A|B) = P(A ∩ B) / P(B) is undefined because you cannot condition on an event that has zero probability (you would be dividing by zero). In practical terms, you can never observe an event that has zero probability, so the notion of “given that B has happened” makes no sense in that scenario.
How does the formula for P(A|A ∪ B) differ from P(A|B)?
P(A|A ∪ B) = P(A) / P(A ∪ B) is conditioning on “either A or B,” whereas P(A|B) = P(A ∩ B) / P(B) is conditioning on “B only.” P(A|B) concentrates on the subset of outcomes where B definitely happened, while P(A|A ∪ B) concentrates on the subset of outcomes where at least one of A or B happened. These are very different conditional spaces, leading to different results.
How can these concepts be applied in machine learning or data science?
In machine learning, conditional probabilities are central to Bayesian methods and to understanding various probabilistic models. For example:
In Bayesian networks, edges typically represent conditional relationships between variables.
In classification problems, you might look at P(Class|Evidence) which is derived from P(Evidence|Class) and P(Class) via Bayes’ theorem.
Real-world interpretability often hinges on understanding how one condition (an input) changes the probability of some outcome or label.
Being fluent in these probability basics is essential for correctly interpreting model outputs, designing experiments, working with Bayesian models, and diagnosing issues like data imbalance or clarifying relationships among features and labels.